
As mathematics students progress through their coursework, they encounter various types of functions, including sinusoidal functions. These functions, commonly represented by sine and cosine waves, can be depicted graphically to visualize their patterns and properties. The unit test on graphs of sinusoidal functions is designed to assess students’ understanding of how to graph and interpret these functions.
The test will cover topics such as the period, amplitude, and phase shift of sinusoidal functions. Students will be expected to correctly identify these characteristics when given an equation or a graph. They will also be asked to sketch the graph of a given sinusoidal function based on its equation, demonstrating their ability to translate mathematical expressions into visual representations.
Additionally, the test will assess students’ understanding of the relationship between the graph of a sinusoidal function and its equation. They will be required to analyze how changes in the equation affect the graph, such as changes in amplitude, period, and phase shift. This will help students develop a deeper understanding of how the parameters in the equation impact the shape and positioning of the graph.
Overall, the unit test on graphs of sinusoidal functions will challenge students to apply their knowledge of trigonometry and function graphing to solve problems and interpret real-world situations. It will test their ability to analyze sinusoidal functions from both algebraic and graphical perspectives, providing a comprehensive assessment of their understanding in this topic.
Understanding Sinusoidal Functions
Sinusoidal functions are a type of mathematical function that model periodic phenomena. These functions are defined by the sine or cosine of an angle, and they can be represented graphically as waves that repeat themselves over a given interval. Understanding sinusoidal functions is essential in various fields, including physics, engineering, and finance, as they allow us to describe and analyze the behavior of cyclical processes.
One key characteristic of sinusoidal functions is their amplitude, which represents the maximum distance between the peak and the equilibrium position of the wave. The amplitude determines the magnitude of the oscillations and can be used to quantify the intensity or strength of a phenomenon. Additionally, sinusoidal functions have a period, which is the length of one complete cycle. The period is related to the frequency of the phenomenon, and it can be used to determine how often the cycle repeats.
When graphing a sinusoidal function, the x-axis usually represents time, while the y-axis represents the value of the function. The graph will show the oscillations of the function as it varies over time. By analyzing the graph, we can determine important information such as the amplitude, period, and phase shift of the sinusoidal function. This information allows us to make predictions about future behavior or analyze specific patterns within the data.
In summary, sinusoidal functions are mathematical representations of periodic phenomena. They allow us to describe and analyze the behavior of cyclical processes and are valuable in various fields. By understanding the amplitude, period, and phase shift of sinusoidal functions, we can gain insights into the underlying patterns and make predictions about future behavior. Graphing sinusoidal functions provides a visual representation of the oscillations and allows for a deeper analysis of the data.
Properties of Sinusoidal Functions
Sinusoidal functions, also known as periodic functions, are a type of mathematical function that exhibit regular patterns and oscillations. These functions are commonly represented by sine or cosine curves and have a number of distinct properties that make them useful in various fields of study, such as physics, engineering, and signal processing.
One important property of sinusoidal functions is their periodicity. A sinusoidal function repeats itself over a certain interval, called the period. This means that the function’s values will repeat after a certain amount of time or distance. The period of a sinusoidal function can be determined by the frequency, which represents the number of complete cycles the function completes in a given unit of time.
Sinusoidal functions also have an amplitude, which represents the maximum displacement or range of values that the function spans. The amplitude determines the height or depth of the function’s oscillations. Additionally, sinusoidal functions can be shifted horizontally or vertically. A horizontal shift, known as phase shift, affects the starting point of the function, while a vertical shift moves the entire function up or down.
Sinusoidal functions are especially useful in modeling various natural phenomena, such as sound waves, light waves, and the motion of pendulums. They are also used in practical applications such as electrical engineering, where they can be used to describe alternating current (AC) signals. By understanding the properties of sinusoidal functions, researchers and engineers can analyze and manipulate these functions to better understand and predict the behavior of the systems they represent.
Graphing Sinusoidal Functions
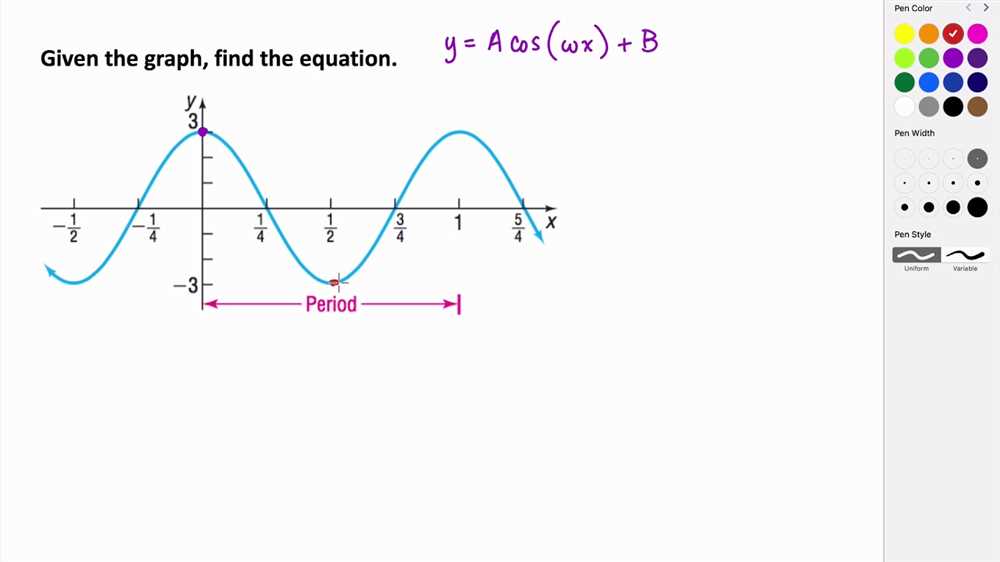
Sinusoidal functions are a type of periodic function that can be represented by a graph of a sine or cosine wave. These functions are commonly used to model various natural phenomena, such as sound waves, light waves, and oscillations in mechanical systems. When graphing sinusoidal functions, it is important to understand their key features and how they can be transformed.
The graph of a sinusoidal function is characterized by its amplitude, period, phase shift, and vertical shift. The amplitude represents the maximum distance that the graph extends above and below its midline. The period is the length of one complete cycle of the function and is equal to 2π divided by the frequency. The phase shift determines how the graph is shifted horizontally, while the vertical shift determines how the graph is shifted vertically.
To graph a sinusoidal function, start by identifying the values of the key features mentioned above. Then, plot key points on the graph using these values. The midline is typically drawn as a horizontal line through the center of the graph. The amplitude determines the maximum and minimum points on the graph. The period is used to determine the length of one complete cycle. Finally, the phase shift and vertical shift are used to shift the graph horizontally and vertically, respectively.
Once these key points are plotted, you can connect them to create a smooth wave-like graph. Remember that sinusoidal functions repeat indefinitely, so you can continue the pattern of the graph beyond the initial cycle. It is also helpful to label the key points and include a scale on the axes to provide context for the graph.
In summary, graphing sinusoidal functions involves understanding their key features and using them to plot key points on the graph. By considering the amplitude, period, phase shift, and vertical shift, you can accurately represent these functions as wave-like graphs. With practice, you can become proficient in graphing and interpreting sinusoidal functions.
Amplitude and Period of Sinusoidal Functions
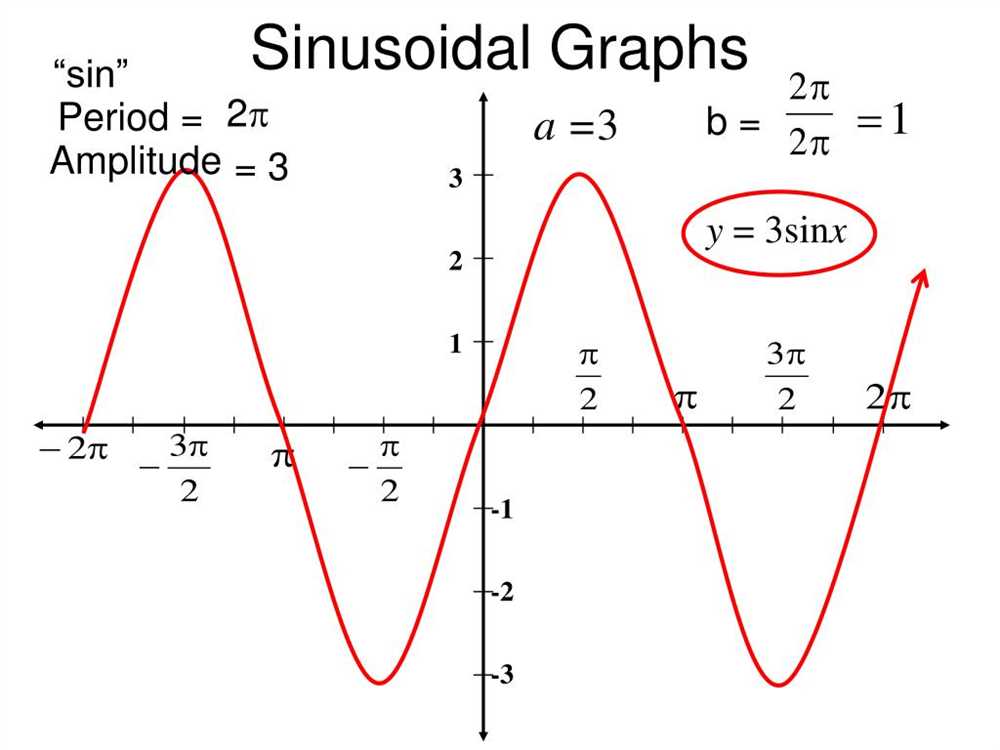
Sinusoidal functions are mathematical representations of waves that oscillate between two extreme values. These functions are commonly represented by equations in the form of y = A sin(Bx + C) + D, where A represents the amplitude, B represents the frequency, C represents a phase shift, and D represents a vertical shift.
The amplitude of a sinusoidal function determines the maximum distance that the graph reaches from its horizontal axis. It is the absolute value of A in the equation, and it signifies the height of the wave. The greater the value of A, the taller the wave will be, and vice versa. The amplitude can be positive or negative, depending on the direction of the wave.
The period of a sinusoidal function determines the length of one complete cycle of the wave. It is calculated using the formula 2π/B, where B is the coefficient of x in the equation. The period represents the horizontal length of the wave and is usually measured in units of distance or time. A smaller value of B will result in a shorter period and a faster oscillation, while a larger value of B will result in a longer period and a slower oscillation.
Understanding the amplitude and period of sinusoidal functions is crucial for analyzing and graphing these types of functions. They provide valuable information about the characteristics of the wave and help in interpreting the data or phenomena represented by the function.
Phase Shift of Sinusoidal Functions

The phase shift can be positive or negative. When C is positive, the graph is shifted to the right, and when C is negative, the graph is shifted to the left. The magnitude of C represents the amount of the shift, with larger values resulting in a greater shift. The shift is measured in the units of the x-axis.
Example:
Consider the equation y = 2*sin(3x – π/4). Here, the value of C is π/12, indicating a phase shift of π/12 units to the right. This means that the graph of the function is shifted to the right by an amount that is equivalent to π/12 units on the x-axis. The vertex (highest or lowest point) of the graph will also be shifted accordingly.
The phase shift of a sinusoidal function is an important concept in analyzing and graphing trigonometric functions. It allows us to determine the starting point of the graph and understand how it is related to the standard position of the parent function.
Vertical and Horizontal Translations of Sinusoidal Functions
Sinusoidal functions are mathematical functions that represent periodic oscillations. These functions can be translated vertically and horizontally, resulting in shifts of the graph. The vertical translation shifts the graph of the function up or down, while the horizontal translation shifts it left or right.
When a sinusoidal function is translated vertically, the entire graph is shifted up or down without changing its shape. The amplitude and period remain the same, but the vertical shift affects the position of the graph. For example, if the function f(x) = sin(x) has a vertical translation of +2, the graph will move upward by 2 units. On the other hand, a vertical translation of -3 will shift the graph downward by 3 units.
Horizontal translations, on the other hand, affect the position of the graph along the x-axis. The amplitude and vertical shift remain the same, but the period changes. A positive horizontal translation shifts the graph to the left, while a negative horizontal translation shifts it to the right. For instance, if the function g(x) = sin(x) has a horizontal translation of +π/4, the graph will move π/4 units to the left. Conversely, a horizontal translation of -π/2 will shift the graph π/2 units to the right.
In summary, vertical translations of sinusoidal functions affect the position of the graph up or down, while horizontal translations shift it left or right. These translations can be represented by adding or subtracting values from the original function. Understanding these translations is important for analyzing and modeling real-life phenomena that exhibit periodic behavior.
Finding Maximum and Minimum Points of Sinusoidal Functions
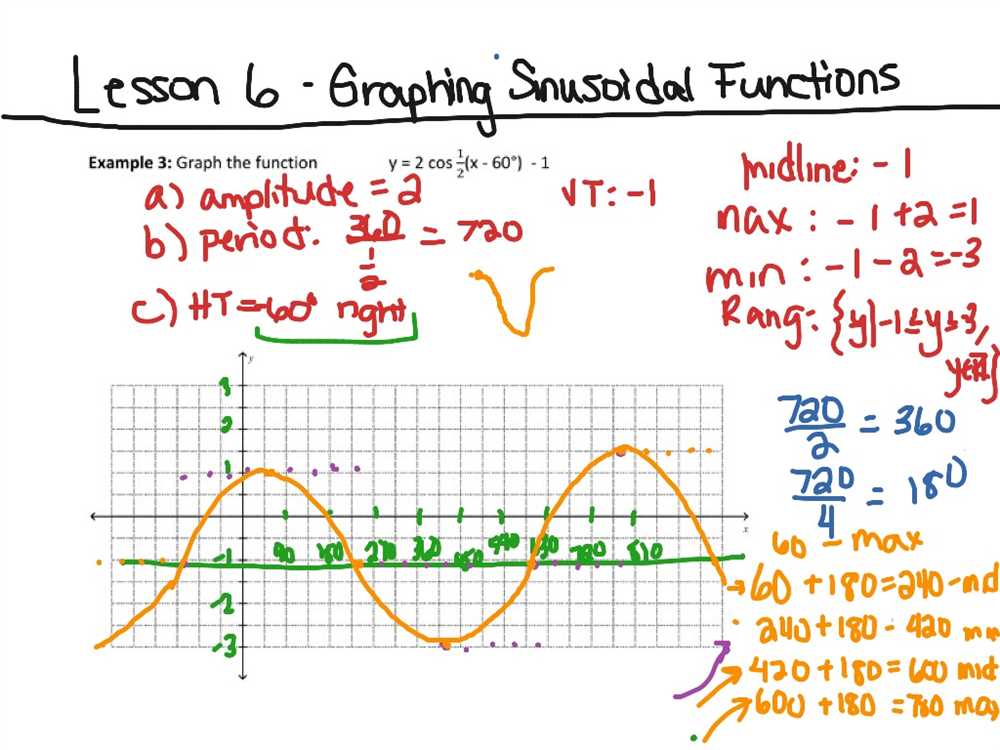
A sinusoidal function is a type of periodic function that can be represented by a sine or cosine graph. These functions have maximum and minimum points that can be found by analyzing their graphs or using mathematical formulas.
One way to find the maximum and minimum points of a sinusoidal function is by examining its graph. The maximum points occur when the function reaches its highest value, while the minimum points occur when the function reaches its lowest value. By observing the graph, you can identify the x-coordinates of these points and then evaluate the function to find the corresponding y-coordinates.
Alternatively, you can use mathematical formulas to find the maximum and minimum points of a sinusoidal function. For a sine function of the form y = a sin(bx + c) + d, the maximum point is given by (c + π/2b, a + d), and the minimum point is given by (c – π/2b, -a + d). Similarly, for a cosine function of the form y = a cos(bx + c) + d, the maximum point is (c, a + d), and the minimum point is (c + π/b, -a + d).
Knowing the maximum and minimum points of a sinusoidal function is important in various applications. These points can help determine the amplitude, period, and phase shift of the function. They also allow us to analyze the behavior of the function and make predictions about its values over time.
Applying Sinusoidal Functions to Real-World Scenarios
Sinusoidal functions, such as sine and cosine, are mathematical representations of cyclic patterns found in nature and various real-world scenarios. By understanding and applying sinusoidal functions, we can analyze and predict behavior in a wide range of fields, including engineering, physics, and biology.
In engineering, sinusoidal functions are often used to model vibrations and oscillations. For example, in mechanical engineering, engineers might use sinusoidal functions to design machinery that operates with controlled vibrations. By manipulating the amplitude, frequency, and phase shift of a sinusoidal function, engineers can optimize the performance of their designs and ensure that they operate within safe and efficient parameters.
In physics, sinusoidal functions are frequently used to describe the motion of objects undergoing periodic motion. For instance, an object attached to a spring experiences a sinusoidal oscillation as it moves back and forth. By analyzing the characteristics of the sinusoidal function representing this motion, physicists can determine important properties such as the object’s period, frequency, and amplitude. This knowledge is crucial in fields such as astrophysics, where understanding the behavior of celestial bodies requires analyzing their periodic motion.
In biology, sinusoidal functions can help us understand biological rhythms and patterns. For instance, the sleep-wake cycle follows a sinusoidal pattern, with periods of increased activity during the day and decreased activity during the night. By studying the sinusoidal function that represents this pattern, researchers can gain insights into the impact of sleep on various physiological processes and develop strategies to optimize sleep and wakefulness.
Overall, applying sinusoidal functions to real-world scenarios allows us to analyze and predict behavior in various scientific and engineering fields. Whether it’s designing machinery, describing oscillatory motion, or understanding biological rhythms, sinusoidal functions provide valuable mathematical tools for understanding and optimizing complex systems.