
If you are looking for additional practice on piecewise defined functions, you have come to the right place. This article provides the answer key to help you check your work and ensure that you have mastered this topic. Piecewise functions are functions that are defined by different rules or formulas on different parts of their domain. They can be quite challenging to work with, but with enough practice, you can become comfortable solving problems involving piecewise defined functions.
By using this answer key, you can compare your solutions to the correct answers and identify any mistakes you might have made. This will help you understand where you went wrong and learn from your errors. It is important to have a strong grasp of piecewise defined functions because they appear in various areas of mathematics, such as calculus and algebra. Mastering these functions will not only improve your problem-solving skills but also deepen your understanding of mathematical concepts.
The answer key provided in this article covers a wide range of problems involving piecewise defined functions. It includes solutions to problems that require evaluating piecewise functions at specific values, finding the domain and range of piecewise functions, and determining the equations of piecewise functions from given graphs or descriptions. The step-by-step solutions will guide you through the process of solving each problem, ensuring that you gain a clear understanding of the concepts involved.
3 Additional Practice Piecewise Defined Functions Answer Key
In this answer key, we will go through three additional practice problems involving piecewise defined functions. These problems will test your understanding of how to evaluate the function for different input values and determine the domain and range of the function. Let’s get started!
Problem 1:
Consider the piecewise defined function:
f(x) =
- 2x + 3, if x ≤ 2
- x^2 + 4, if x > 2
To evaluate this function for different input values, we need to consider the value of x and determine which part of the function to use. If x is less than or equal to 2, we use the first part of the function, 2x + 3. If x is greater than 2, we use the second part of the function, x^2 + 4. For example, if we want to find f(1), we would substitute 1 into the first part of the function, resulting in f(1) = 2(1) + 3 = 5.
The domain of the function is determined by the values of x for which the function is defined. In this case, the function is defined for all real numbers, so the domain is (-∞, ∞).
The range of the function is the set of all possible output values. To determine the range, we need to consider the possible values of the function for different input values. In this case, since the first part of the function is a linear equation and the second part is a quadratic equation, the range is (-∞, ∞) for both parts of the function.
Problem 2:
Consider the piecewise defined function:
g(x) =
- 3x + 2, if x < -1
- x^3, if -1 ≤ x ≤ 1
- 2x – 1, if x > 1
To evaluate this function for different input values, we need to consider the value of x and determine which part of the function to use. We follow the same process as in Problem 1. For example, if we want to find g(0), we would substitute 0 into the second part of the function, resulting in g(0) = 0^3 = 0.
The domain of the function is determined by the values of x for which the function is defined. In this case, the function is defined for all real numbers, so the domain is (-∞, ∞).
The range of the function is the set of all possible output values. In this case, since the first part of the function is a linear equation, the second part is a cubic equation, and the third part is another linear equation, the range is (-∞, ∞) for all three parts of the function.
Problem 3:
Consider the piecewise defined function:
h(x) =
- 2x + 4, if x ≤ -2
- -x^2, if -2 < x ≤ 0
- 3x – 1, if x > 0
To evaluate this function for different input values, we need to consider the value of x and determine which part of the function to use. We follow the same process as in the previous problems. For example, if we want to find h(-3), we would substitute -3 into the first part of the function, resulting in h(-3) = 2(-3) + 4 = -2.
The domain of the function is determined by the values of x for which the function is defined. In this case, the function is defined for all real numbers, so the domain is (-∞, ∞).
The range of the function is the set of all possible output values. In this case, since the first part of the function is a linear equation, the second part is a quadratic equation, and the third part is another linear equation, the range is (-∞, ∞) for all three parts of the function.
Overall, piecewise defined functions involve breaking a function into different parts based on the value of the input, and evaluating each part separately. By understanding the rules for evaluating piecewise defined functions and determining their domain and range, you can effectively solve problems involving these types of functions.
Overview
In mathematics, piecewise defined functions are functions that are defined by different rules or formulas on different intervals or domains. These functions are often used to describe real-world situations that have different behaviors or conditions in different regions. By breaking down the problem into different cases, piecewise defined functions provide a more accurate representation of the situation.
When dealing with piecewise defined functions, it is important to understand the different rules or formulas that apply to each interval. This allows us to evaluate the function and determine its behavior in different regions. Graphically, piecewise defined functions are often represented by a series of connected line segments or curves, where each segment represents the function’s behavior in a specific interval.
In this practice exercise, we will be working with piecewise defined functions and exploring their properties. We will focus on evaluating the function at different points, determining its domain and range, and graphing it on a coordinate plane. By practicing these skills, we can improve our understanding of piecewise defined functions and develop our problem-solving abilities in this area.
Let’s dive into the exercise and discover the intricacies of piecewise defined functions!
Understanding Piecewise Defined Functions
Piecewise defined functions are mathematical functions that are defined differently depending on the value of the input variable. They consist of different “pieces” or sections, each with its own set of rules or equations. This allows the function to behave differently in different intervals or regions.
One way to represent piecewise functions is through the use of if-then statements. Each section of the function is defined using an if-then statement, where a specific condition is checked and a corresponding equation is used if the condition is true. If none of the conditions are true, a default equation can be used to cover all other cases.
For example, consider the piecewise function f(x) defined as:
- f(x) = x + 1 if x < 0
- f(x) = x^2 if 0 ≤ x ≤ 1
- f(x) = 2x – 1 if x > 1
In this case, if the input x is less than 0, the equation f(x) = x + 1 is used. If x is between 0 and 1 (inclusive), the equation f(x) = x^2 is used. And if x is greater than 1, the equation f(x) = 2x – 1 is used.
Understanding piecewise defined functions is important in various areas of mathematics, including calculus, algebra, and statistics. They allow for more flexibility in representing complex mathematical relationships and can help solve real-world problems that involve different cases or conditions.
Solving Piecewise Defined Functions
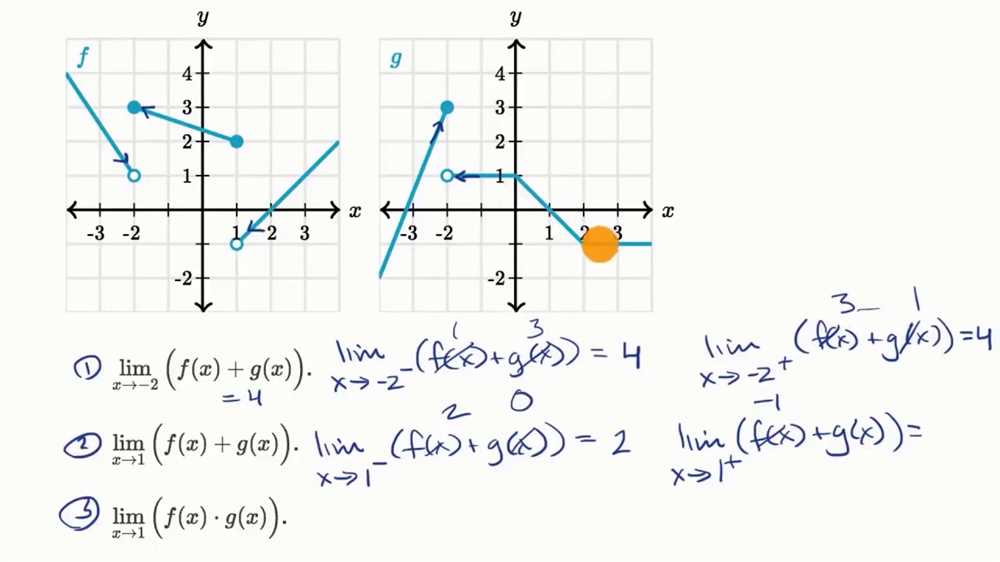
A piecewise defined function is a mathematical function that is defined by different expressions or formulas for different intervals or subsets of its domain. Solving a piecewise function involves finding the appropriate expression or formula to use for a given input value or interval.
When solving a piecewise function, it is important to identify the intervals or subsets of the domain where different expressions or formulas apply. This can usually be done by looking at the conditions or inequalities associated with each expression or formula in the definition of the function. Once the intervals are identified, the appropriate expression can be used to evaluate the function for a given input value or interval.
For example, consider the piecewise defined function:
f(x) = {
3x, if x < 1
2x + 1, if 1 ≤ x ≤ 3
x^2, if x > 3
}
To solve this function, we need to determine the expression to use based on the given input value or interval. If the input value is less than 1, we use the expression 3x. If the input value is between 1 and 3 (inclusive), we use the expression 2x + 1. If the input value is greater than 3, we use the expression x^2.
Let’s say we want to find the value of f(2). Since 2 is between 1 and 3, we use the expression 2x + 1. Plugging in the value of x = 2, we get:
f(2) = 2(2) + 1 = 5
Therefore, f(2) = 5.
In summary, solving a piecewise defined function involves identifying the intervals or subsets of the domain where different expressions or formulas apply, and then using the appropriate expression or formula to evaluate the function for a given input value or interval. This can be done by carefully analyzing the conditions or inequalities associated with each expression in the definition of the function.
Working with Piecewise Functions in Graphing
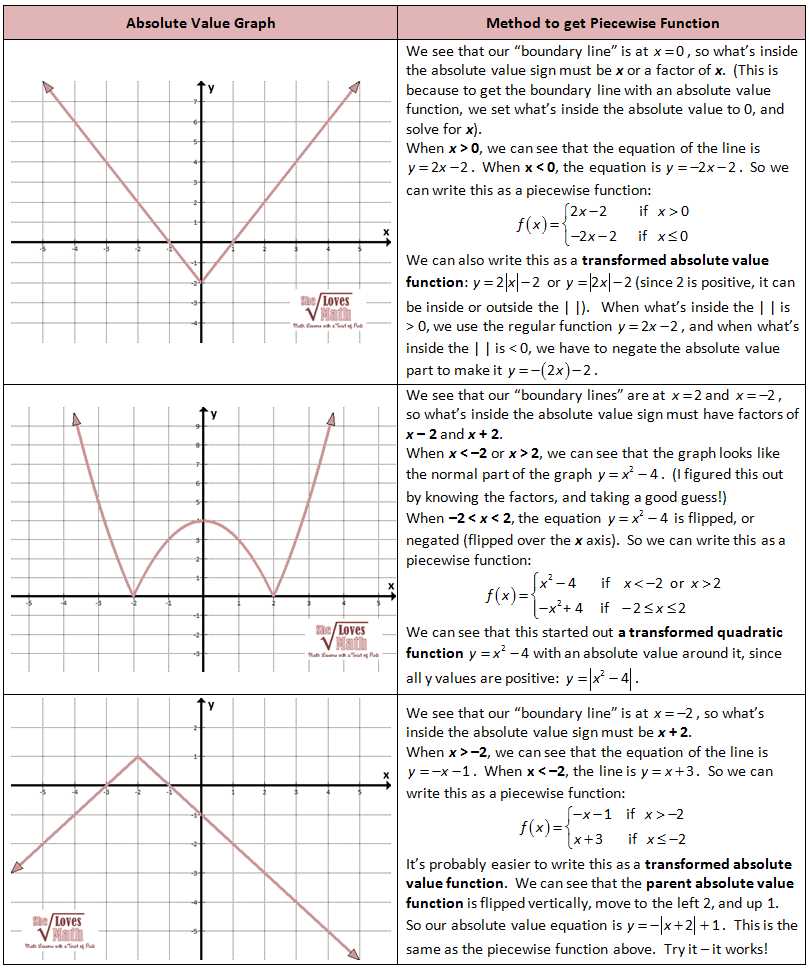
When working with piecewise functions, it is important to understand how to graph them accurately. Piecewise functions are functions that are defined differently depending on the input value. This means that they have different rules or formulas for different intervals or subsets of the input domain. Graphing piecewise functions requires careful analysis of these intervals and rules to accurately represent the function on a graph.
To graph a piecewise function, it is helpful to identify the different intervals or subsets of the input domain and their corresponding rules or formulas. These rules can be represented by equations or inequalities. Once the rules are identified, the graph can be constructed by plotting points or sketching the function based on the rules.
One important consideration when graphing piecewise functions is the continuity or smoothness of the graph. Piecewise functions can have points or lines that are disconnected from each other, creating discontinuities. These discontinuities can be classified as removable or nonremovable based on how they affect the function’s behavior. It is important to identify and understand these discontinuities to accurately graph the function.
Another aspect to consider when working with piecewise functions in graphing is the limitations of the graphing tools or software available. Some software may not be able to handle the complexity of certain piecewise functions, especially those with multiple rules or formulas. In such cases, it might be necessary to break down the piecewise function into simpler components or use other graphing techniques to accurately represent the function.
Overall, working with piecewise functions in graphing requires a solid understanding of the different rules or formulas, the intervals or subsets of the input domain, and the potential discontinuities. By carefully analyzing these elements and using appropriate graphing techniques, one can accurately represent piecewise functions on a graph.
Using Piecewise Defined Functions in Real Applications
Piecewise defined functions are a powerful mathematical tool that allow us to model and analyze real-life scenarios that involve different rules or conditions. By breaking down a problem into separate parts and defining different functions for each part, we can accurately represent complex relationships and make predictions based on specific conditions.
One real-life application of piecewise defined functions is in the field of finance. For example, when analyzing the profitability of an investment, we may have different rules or formulas for calculating returns depending on the time period or the amount invested. By using a piecewise defined function, we can account for these different conditions and accurately calculate the overall return on investment.
Another application of piecewise defined functions is in computer programming. Many programming languages allow the use of if-else statements, which can be thought of as piecewise defined functions. These statements allow the program to execute different code blocks based on specific conditions or user inputs. By using piecewise defined functions in programming, we can create complex and dynamic algorithms that respond to different scenarios or inputs.
Furthermore, piecewise defined functions are used in areas such as physics, engineering, and statistics. For example, in physics, different laws or equations may apply depending on the position or velocity of an object. By using piecewise defined functions, we can accurately model the behavior of the object and make predictions about its motion. In engineering, piecewise defined functions can be used to model different operating modes or conditions of a system and optimize its performance. In statistics, piecewise defined functions can be used to model different groups or subpopulations and analyze their characteristics separately.
In conclusion, piecewise defined functions are a versatile tool that can be used in various real-life applications. By breaking down complex problems into separate parts and defining different functions for each part, we can accurately represent different conditions and make predictions based on specific scenarios. Whether in finance, computer programming, physics, engineering, or statistics, piecewise defined functions provide a powerful and flexible framework for understanding and solving real-world problems.
Extra Practice Problems
Here are some additional practice problems to help you further develop your skills in working with piecewise defined functions:
Problem 1:
Write a piecewise defined function for the following situation:
– For all values of x less than or equal to 0, the function is equal to the square of x.
– For all values of x greater than 0, the function is equal to the absolute value of x.
Solution:
The piecewise defined function for this situation can be written as follows:
f(x) = x^2, if x ≤ 0
f(x) = |x|, if x > 0
Problem 2:
Consider the following piecewise defined function:
f(x) = 2x, if x < 1
f(x) = x^2, if 1 ≤ x ≤ 3
f(x) = 3, if x > 3
a) Find the value of f(0).
Solution:
Since 0 is less than 1, we use the first equation of the piecewise defined function:
f(0) = 2(0) = 0
b) Find the value of f(2).
Solution:
Since 2 is between 1 and 3, we use the second equation of the piecewise defined function:
f(2) = (2)^2 = 4
c) Find the value of f(4).
Solution:
Since 4 is greater than 3, we use the third equation of the piecewise defined function:
f(4) = 3
These extra practice problems will help you strengthen your understanding of working with piecewise defined functions. Keep practicing and you’ll become more confident in solving various problems involving these functions!