
Mathematics plays a crucial role in our everyday lives, and understanding geometric concepts is essential for solving real-world problems. One fundamental concept in geometry is the measurement of shapes, which includes finding the perimeter, circumference, and area. The 1 8 perimeter circumference and area worksheet answer key is a valuable resource that helps students master these concepts and practice their problem-solving skills.
The worksheet provides a set of challenging problems that require students to calculate the perimeter, circumference, and area of various shapes, such as triangles, rectangles, circles, and irregular polygons. By using formulas and applying logical thinking, students can determine the lengths of sides, diameters, and radii, and then find the required measurements. The answer key serves as a guide, providing step-by-step solutions and explanations for each problem.
By using the 1 8 perimeter circumference and area worksheet answer key, students can enhance their understanding of geometric concepts and develop their critical thinking skills. The key allows them to analyze their mistakes, learn from them, and improve their problem-solving strategies. This resource also helps teachers assess their students’ knowledge and identify areas that need further clarification or reinforcement.
Understanding Perimeter
The concept of perimeter is fundamental in geometry and is crucial for understanding the size and shape of various objects. Perimeter is defined as the distance around the boundary of a two-dimensional shape. It can be thought of as the sum of all the sides of a shape.
Calculating Perimeter: To calculate the perimeter of a shape, you simply add up the lengths of all its sides. This applies to both regular and irregular shapes. It is important to pay attention to the units used for the sides, as the perimeter will be in the same unit.
For example:
- A rectangle with sides of lengths 6 cm and 8 cm will have a perimeter of 28 cm (6 + 8 + 6 + 8).
- A triangle with sides of lengths 3 cm, 4 cm, and 5 cm will have a perimeter of 12 cm (3 + 4 + 5).
Applications of Perimeter: Understanding perimeter is essential in various real-life situations. For example, when planning a garden or fence, knowing the perimeter of the area you want to enclose will help you determine how much material you need. Similarly, when measuring the length of a piece of furniture or a room, you are essentially finding the perimeter.
Moreover, understanding perimeter is important for more advanced topics in geometry, such as finding the area of irregular shapes or calculating the circumference of circles. By grasping the concept of perimeter, you lay the foundation for tackling more complex geometric problems.
Finding the Circumference
The circumference is a fundamental measurement in geometry that represents the distance around a circular object. It is an important concept in various fields, such as engineering, architecture, and physics. Understanding how to find the circumference of a circle is essential for solving problems involving circles and circular objects.
To find the circumference of a circle, you need to know the radius or the diameter of the circle. The radius is the distance from the center of the circle to any point on its circumference, while the diameter is the distance across the circle passing through its center.
To calculate the circumference using the radius:
- Multiply the radius by 2 to get the diameter.
- Multiply the diameter by π (pi), which is approximately 3.14159.
To calculate the circumference using the diameter:
- Multiply the diameter by π (pi), which is approximately 3.14159.
The formula for calculating the circumference of a circle is:
Circumference = 2πr (using the radius)
Circumference = πd (using the diameter)
It is important to note that the circumference is always proportional to the diameter or radius of the circle. This means that if you double the radius or diameter, the circumference will also double. The circumference is measured in units of length, such as centimeters, inches, or meters.
Overall, knowing how to find the circumference of a circle is essential for various applications in math and everyday life. It allows us to calculate distances, design objects, and solve problems involving circular shapes.
Calculating Area
When it comes to measuring the area of different shapes, it is important to understand the formulas and methods used for calculation. By determining the area, we are able to quantify the amount of space enclosed by a particular shape.
Rectangle and Square: The area of a rectangle or square can be calculated by multiplying the length of one side by the length of the adjacent side. The formula for the area of a rectangle is: Area = Length × Width.
Triangle: To find the area of a triangle, we can use the formula: Area = 1/2 × Base × Height. The base is the length of one side of the triangle, and the height is the distance from the base to the opposite vertex.
Circle: Calculating the area of a circle involves using the formula: Area = π × radius^2. The radius is the distance from the center of the circle to any point on its edge, and π (pi) is a mathematical constant approximately equal to 3.14159.
Irregular Shapes: Non-geometric shapes or irregular shapes can also have their areas calculated using different methods. One common approach is to divide the shape into smaller, regular shapes with known formulas. By calculating the area of each smaller shape and summing them together, we can determine the total area of the irregular shape.
In conclusion, calculating the area of different shapes requires understanding the specific formulas and methods associated with each shape. By applying these formulas, we can accurately measure and quantify the space enclosed by a given shape.
Perimeter, Circumference, and Area Formulas
The concept of perimeter, circumference, and area is fundamental to understanding geometric shapes and their measurements. These formulas provide us with a way to calculate the length, distance, and size of various objects.
Perimeter: The perimeter of a shape is the total length of all its sides. To find the perimeter of a polygon, simply add up the lengths of all its sides. The formula for perimeter P is:
P = s1 + s2 + s3 + … + sn
Where s1, s2, s3, … sn are the lengths of the individual sides of the polygon.
Circumference: The circumference of a circle is the distance around its outer edge. To find the circumference of a circle, we use the formula:
C = 2πr
Where C is the circumference, π (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
Area: The area of a shape is the amount of space it occupies. Area can be calculated differently for different shapes. Here are a few common formulas:
- Square: A square’s area is found by squaring the length of one of its sides. The formula is: A = s^2, where A is the area and s is the length of the side.
- Rectangle: A rectangle’s area is found by multiplying its length and width. The formula is: A = l × w, where A is the area, l is the length, and w is the width.
- Triangle: A triangle’s area is found by multiplying its base length and height, and then dividing by 2. The formula is: A = 0.5 × b × h, where A is the area, b is the base length, and h is the height.
- Circle: A circle’s area is found by multiplying π (pi) by the square of its radius. The formula is: A = πr^2, where A is the area and r is the radius.
These formulas are essential tools for solving problems related to shapes, measurements, and geometry. By understanding and applying these formulas, we can accurately calculate the perimeter, circumference, and area of various objects and shapes.
Using the Worksheet
The “1 8 perimeter circumference and area worksheet” is a valuable tool for students to practice and enhance their understanding of perimeter, circumference, and area calculations. This worksheet provides a variety of exercises that require students to apply the formulas and concepts learned in class to solve real-life problems. By working through these exercises, students can develop their problem-solving skills and reinforce their understanding of these mathematical concepts.
The worksheet includes a range of different types of questions, such as finding the perimeter of polygons, calculating the circumference of circles, and determining the area of various shapes. Each question is accompanied by clear instructions and examples to help students understand the process and methodology required to solve the problem. In addition, the answer key at the end of the worksheet allows students to check their work and verify their solutions.
To effectively use the worksheet, students should carefully read each question and identify the relevant formula or concept that needs to be applied. They should then apply the appropriate formula to calculate the perimeter, circumference, or area. It is important for students to show their work and clearly label their answers. This will help the student and the teacher to review and assess their understanding of the material.
The “1 8 perimeter circumference and area worksheet” can be used as a standalone practice exercise or as a supplement to classroom instruction. Teachers can assign the worksheet as homework, in-class work, or even as a review activity before an exam. By regularly using this worksheet, students can strengthen their skills in perimeter, circumference, and area calculations and improve their overall mathematical competence.
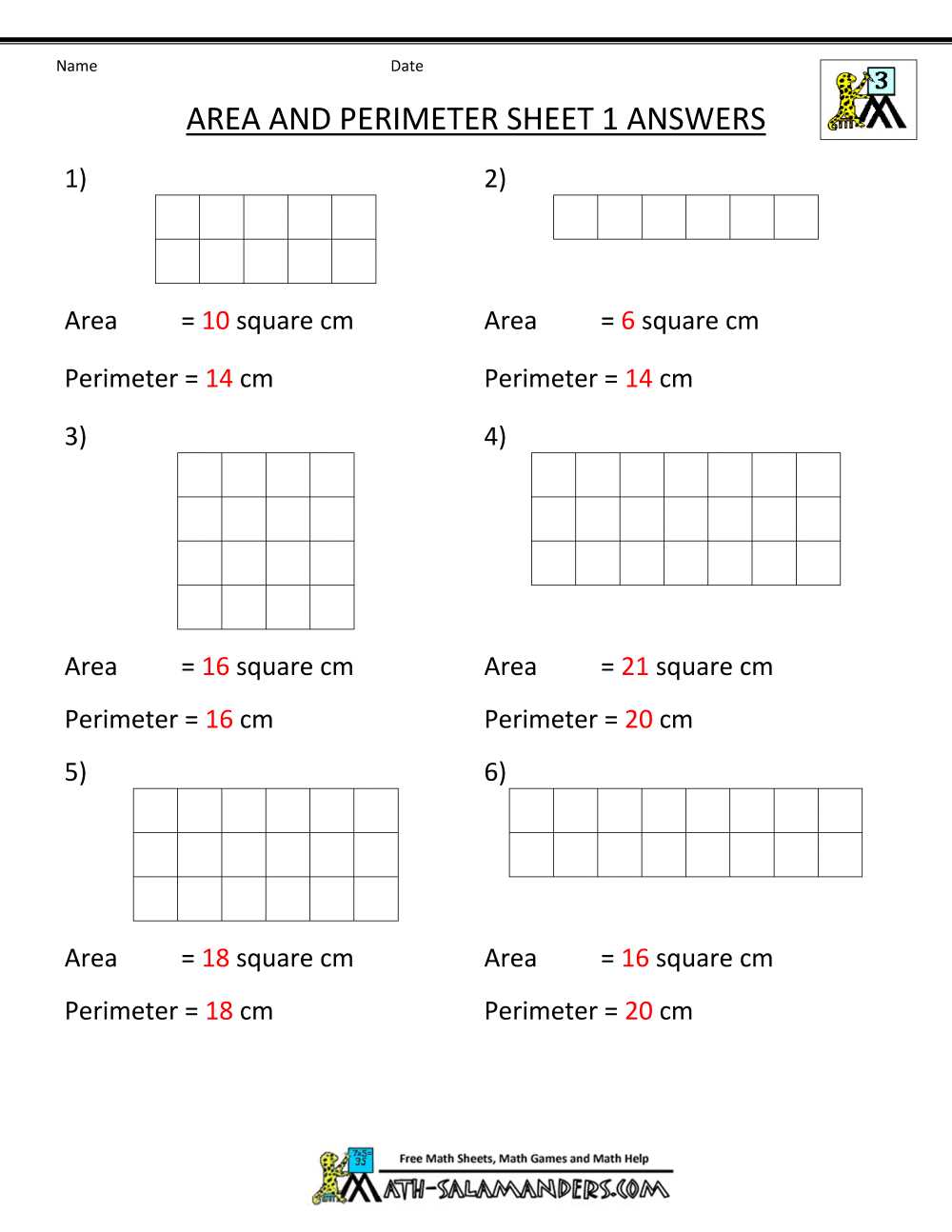
Answer Key for Perimeter Questions

In the study of geometry, one important concept is perimeter. The perimeter of a shape is the total distance around its outer edge. To find the perimeter of a shape, you need to add up the lengths of all its sides. The answer key for perimeter questions provides the correct answers for various perimeter problems, allowing students to check their work and ensure they are on the right track.
The answer key includes step-by-step solutions for different types of perimeter questions. It covers basic shapes such as rectangles, squares, triangles, and circles. Each question is accompanied by the correct formula and calculation method for finding the perimeter. This can be a helpful tool for students who are learning how to apply formulas and solve perimeter problems.
Example:
- Question: Find the perimeter of a rectangle with length 10 cm and width 5 cm.
- Solution: Perimeter = 2(length + width) = 2(10 + 5) = 2(15) = 30 cm.
The answer key for perimeter questions not only provides the final answer but also guides students through the correct steps to solve the problem. It is a valuable resource for teachers as well, as it allows them to easily evaluate their students’ understanding of perimeter concepts and identify areas where further instruction may be needed.
Overall, the answer key for perimeter questions is an essential tool for both students and teachers in the study of geometry. It helps ensure accuracy and provides a clear understanding of how to solve perimeter problems.
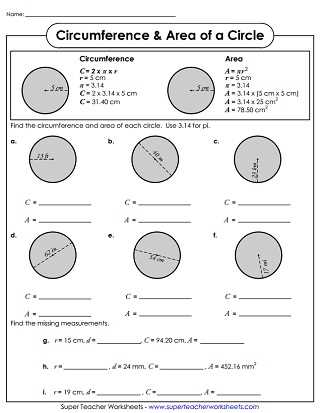
Answer Key for Circumference Questions
In mathematics, circumference is the distance around the edge of a circle. It is an important concept that is often covered in geometry classes. Calculating the circumference of a circle requires knowing the radius or diameter of the circle, and using the formula C = πd or C = 2πr, where C represents the circumference, π represents the mathematical constant pi (approximately 3.14159), and d and r represent the diameter and radius of the circle, respectively.
Answer keys for circumference questions can be helpful for students to check their work and ensure they are correctly applying the formulas and calculations. By referring to the answer key, students can verify if their answers are correct and identify any errors in their calculations. It can also serve as a valuable learning tool, allowing students to see the correct steps and approach to solving circumference problems.
When providing an answer key for circumference questions, it is important to clearly indicate the correct answers and provide any necessary explanations or steps involved. This can be done through formatting the answer key in a clear and organized manner, using headings, bullet points, and tables if necessary. The answer key should also include the correct units of measurement, as circumference is typically measured in units such as inches, centimeters, or meters.
Example Answer Key for Circumference Questions:
- Question 1: What is the circumference of a circle with a diameter of 8 inches?
- Answer: Using the formula C = πd, the circumference is C = 3.14159 * 8 = 25.13272 inches.
- Question 2: Find the circumference of a circle with a radius of 5 centimeters.
- Answer: Using the formula C = 2πr, the circumference is C = 2 * 3.14159 * 5 = 31.4159 centimeters.
By providing a clear and concise answer key, students can effectively check their work and gain a better understanding of circumferences in geometry. Practice with answer keys can also help reinforce the concept and improve problem-solving skills.
Answer Key for Area Questions
When solving problems related to area, it is important to have an answer key to check your work and ensure accuracy. The answer key for area questions provides a reference point for students and teachers to compare their solutions and verify if they are correct. It allows for immediate feedback and helps in identifying any mistakes or misconceptions.
The answer key typically includes the correct numerical value for the area, as well as the units of measurement. It may also include step-by-step calculations or explanations to show the process of finding the area. This can be particularly helpful for students who are learning the concept for the first time or struggling with the calculations.
The answer key for area questions can be presented in various formats, such as a table or a list. For example, in a table format, the questions and their corresponding answers can be organized in separate columns. This allows for easy comparison and identification of correct answers. Alternatively, in a list format, the questions can be numbered and listed with their respective answers.
Overall, the answer key for area questions serves as a valuable tool for students and teachers alike. It promotes learning and understanding by providing immediate feedback and allowing for self-assessment. It also helps in building confidence and reinforcing the correct methods of finding the area. By utilizing the answer key, students can effectively check their work, identify mistakes, and improve their problem-solving skills.