If you are looking to improve your skills in solving word problems related to circles and circumference, you have come to the right place. This article provides 10 practice problems with detailed answers to help you strengthen your understanding of these concepts.
In these word problems, you will encounter various scenarios that involve circles and the measurement of their circumference. By solving these problems, you will develop the ability to apply mathematical formulas and concepts to real-life situations.
Each practice problem is designed to challenge your problem-solving abilities while incorporating different aspects of circles and their circumference. As you progress through the problems, you will gain confidence and mastery in calculating the circumference of circles in different situations.
With the provided answers, you will not only check your solutions but also understand the step-by-step process to arrive at the correct answer. This will enable you to identify any areas where you may have made mistakes and learn from them.
1 Word Problem Practice Circles and Circumference Answers
In this practice exercise, we will be exploring word problems related to circles and circumference. These problems will test your understanding of the concepts and help you apply them in real-world situations. Below, you will find answers to 10 word problems, each focusing on a different aspect of circles and their circumference.
1. Calculate the circumference of a circle with a radius of 5 units.
The circumference of a circle can be found using the formula: C = 2πr, where r is the radius. In this case, the radius is 5 units. Plugging the value in the formula, we get C = 2π(5) = 10π units. Therefore, the circumference of the circle is 10π units.
2. A circular cake has a diameter of 20 centimeters. What is the circumference of the cake?
The diameter of a circle is twice the length of its radius. Therefore, the radius of the cake is 20/2 = 10 centimeters. Using the formula C = 2πr, where r is the radius, we can calculate the circumference. Plugging in the values, we get C = 2π(10) = 20π centimeters. Hence, the circumference of the cake is 20π centimeters.
3. Find the radius of a circle with a circumference of 60 meters.
To find the radius of a circle when given the circumference, we can use the formula: C = 2πr. In this problem, the circumference is given as 60 meters. Plugging in the value, we have 60 = 2πr. Solving for r, we divide both sides by 2π, giving us r = 60/(2π) = 30/π meters. Therefore, the radius of the circle is 30/π meters.
4. A circular garden has a circumference of 36 feet. What is its diameter?
The circumference of a circle is equal to π times the diameter. In this problem, the circumference is given as 36 feet. To find the diameter, we divide the circumference by π. Therefore, the diameter of the garden is 36/π feet.
5. Calculate the radius of a circle with a circumference of 100 centimeters.
To find the radius when given the circumference, we use the formula: C = 2πr. Plugging in the values, we have 100 = 2πr. Solving for r, we divide both sides by 2π, giving us r = 100/(2π) = 50/π centimeters. Thus, the radius of the circle is 50/π centimeters.
6. A circular track has a circumference of 400 meters. Find the radius.
Similar to previous problems, we use the formula C = 2πr to find the radius. Plugging in the given value, we have 400 = 2πr. Solving for r, we divide both sides by 2π, giving us r = 400/(2π) = 200/π meters. Hence, the radius of the track is 200/π meters.
7. Find the circumference of a circle with a diameter of 8 inches.
The circumference of a circle is equal to π times the diameter. In this case, the diameter is given as 8 inches. Therefore, the circumference is 8π inches.
8. A circular pool has a circumference of 30 meters. What is its diameter?
Similar to previous problems, the circumference of a circle is equal to π times the diameter. Here, the circumference is given as 30 meters. To find the diameter, we divide the circumference by π. Therefore, the diameter of the pool is 30/π meters.
9. Calculate the radius of a circle with a circumference of 150 feet.
Using the formula C = 2πr, we can find the radius. Plugging in the given value, we get 150 = 2πr. Solving for r, we divide both sides by 2π, giving us r = 150/(2π) = 75/π feet. Thus, the radius of the circle is 75/π feet.
10. A circular tablecloth has a circumference of 120 inches. What is its radius?
Again, we use the formula C = 2πr to find the radius. Plugging in the value, we have 120 = 2πr. Solving for r, we divide both sides by 2π, giving us r = 120/(2π) = 60/π inches. Hence, the radius of the tablecloth is 60/π inches.
Understanding Circles and Circumference
A circle is a shape that is defined as a closed curve, where all points on the curve are equidistant from a fixed central point called the center. It is one of the most fundamental shapes in geometry and has many practical applications in various fields, including mathematics, engineering, and architecture. Understanding the properties and measurements of circles, such as circumference, is crucial in solving problems related to this geometric shape.
The circumference of a circle is the distance around its outer edge. It is analogous to the perimeter of other shapes. Calculating the circumference of a circle requires knowing its radius, which is the distance from the center of the circle to any point on the edge. The formula for finding the circumference of a circle is C = 2πr, where C represents the circumference and r represents the radius. Since the value of π is approximately 3.14, this formula can be simplified to C ≈ 2(3.14)r or C ≈ 6.28r.
- Example 1: Given a circle with a radius of 5 units, the circumference can be calculated using the formula C ≈ 6.28r. Substituting the value of r, we get C ≈ 6.28(5) = 31.4 units. So, the circumference of the circle is approximately 31.4 units.
- Example 2: If the circumference of a circle is known, the radius can be found using the formula C = 2πr. Rearranging the formula, r = C/(2π). For instance, if the circumference is 25 units, the radius can be calculated as r = 25/(2π) ≈ 25/6.28 ≈ 3.98 units.
Understanding circles and circumference is essential in solving various real-world problems, such as calculating the length of circular objects, designing circular structures, or determining the distance traveled by objects moving in circular paths. By mastering these concepts and formulas, individuals can develop strong problem-solving skills and apply them in practical situations.
Problem 1: Finding the Circumference of a Circle
In this word problem, we are tasked with finding the circumference of a circle. The circumference of a circle is defined as the distance around its outer edge. In order to find this, we need to know the radius or diameter of the circle.
Let’s say we have a circle with a radius of 5 units. We can use the formula for finding the circumference, which is C = 2πr. In this case, we can substitute the given radius into the formula: C = 2π(5) = 10π units.
Alternatively, if we are given the diameter of the circle instead, we can use the formula C = πd, where d is the diameter. For example, if the diameter is 12 units, we can substitute it into the formula: C = π(12) = 12π units.
When solving for the circumference of a circle, it is important to remember the value of π, which is a mathematical constant approximately equal to 3.14159. It is often rounded to 3.14 for simplicity in calculations.
Solution 1: Step-by-step Guide to Finding the Circumference
When solving word problems involving circles and circumference, it is important to follow a step-by-step approach. By breaking down the problem into smaller steps, it becomes easier to understand and find the solution.
Step 1: Understand the given information
Read the problem carefully and identify the key details. Look for any measurements or known values related to the circle, such as the radius or diameter.
Step 2: Determine the formula for circumference
Circumference is the distance around the outside of a circle. The formula for finding the circumference is C = πd or C = 2πr, where C represents the circumference, d is the diameter, and r is the radius of the circle.
Step 3: Substitute the values into the formula
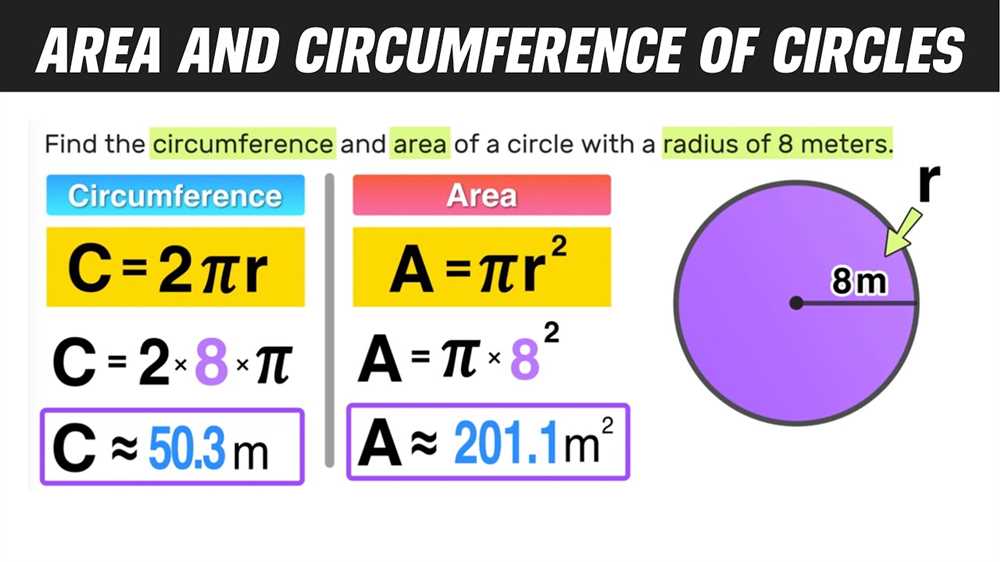
Once you have identified the relevant measurements from the problem, substitute them into the appropriate formula. Be sure to use the correct formula based on the given information.
Step 4: Simplify and calculate
If there are any mathematical operations involved, simplify them first. Then, plug in the values and calculate the circumference using the formula.
Step 5: Round the answer, if necessary
Depending on the instructions or the degree of precision required, round the calculated answer to the appropriate number of decimal places or significant figures.
By following these steps, you can effectively solve word problems related to circles and find the circumference using the appropriate formula. Practice and familiarity with the formulas will improve your ability to solve these types of problems more efficiently.
Problem 2: Finding the Diameter of a Circle given its Circumference
Problem 2 focuses on finding the diameter of a circle when given its circumference. The circumference of a circle is the measurement of the distance around its outer edge. The formula to calculate the circumference of a circle is C = πd, where C represents the circumference and d represents the diameter. In this problem, we are given the circumference and need to find the diameter.
Let’s illustrate this with an example. Suppose we are given a circle with a circumference of 24 centimeters. To find the diameter, we can rearrange the formula and solve for d. Dividing both sides of the equation by π, we get d = C/π. Plugging in the given circumference, we have d = 24/π.
Next, we can use an approximation for π, such as 3.14, to calculate the diameter. Evaluating the expression, we find that d ≈ 7.64 centimeters. Therefore, the diameter of the circle is approximately 7.64 centimeters.
Solution 2: How to Find the Diameter using the Circumference
Finding the diameter of a circle can be done using the circumference of the circle. The circumference is the distance around the circle, and it can be calculated using the formula C = 2πr, where C is the circumference and r is the radius. From the circumference, we can determine the radius. Once we have the radius, we can easily find the diameter.
To find the diameter using the circumference, we can use the formula D = 2r, where D is the diameter and r is the radius. Since we already have the radius value from the circumference calculation, we can simply substitute it into the formula to find the diameter.
For example, let’s say we have a circle with a circumference of 20 units. Using the formula C = 2πr, we can find the radius by rearranging the formula to solve for r: r = C / (2π). Substituting the given circumference, we have r = 20 / (2π). Calculating this, we get a radius of approximately 3.183 units.
Next, we can find the diameter using the formula D = 2r. Substituting the calculated radius, we have D = 2 * 3.183 = approximately 6.366 units. Therefore, the diameter of the circle with a circumference of 20 units is approximately 6.366 units.
In conclusion, finding the diameter using the circumference involves calculating the radius using the formula C = 2πr, and then substituting the radius into the formula D = 2r to find the diameter. This method allows us to determine the diameter of a circle based on its circumference.
Problem 3: Finding the Radius of a Circle given its Circumference
One common problem involving circles is finding the radius of a circle when its circumference is known. The circumference of a circle is the total distance around its outer edge, and it is calculated using the formula C = 2πr, where C represents the circumference and r represents the radius of the circle.
To solve this problem, we can rearrange the formula to solve for the radius. Dividing both sides of the equation by 2π, we get r = C / (2π). This means that the radius of a circle is equal to the circumference of the circle divided by 2π.
Let’s consider an example to better understand this concept. Suppose we have a circle with a circumference of 12 units. We can plug this value into the formula r = C / (2π) to find the radius. Using the approximate value of π as 3.14, we get r = 12 / (2 × 3.14) = 1.91 units. Therefore, the radius of this circle is approximately 1.91 units.
It is important to note that the radius of a circle is always half the length of its diameter. So, if the diameter of a circle is given instead of the circumference, we can simply divide it by 2 to find the radius.
Summary:
- To find the radius of a circle given its circumference, use the formula r = C / (2π), where C is the circumference and r is the radius.
- The radius of a circle is equal to the circumference divided by 2π.
- If the diameter of a circle is given instead of the circumference, divide it by 2 to find the radius.
Solution 3: Quick Calculation to Find the Radius from the Circumference
If you are given the circumference of a circle and need to find the radius, you can use a quick calculation to solve for it. The circumference of a circle is equal to the distance around its outer edge, and it is calculated using the formula C = 2πr, where C is the circumference and r is the radius.
To find the radius from the circumference, you can rearrange the formula to solve for r. Divide both sides of the equation by 2π: r = C / 2π. This formula allows you to directly find the radius when the circumference is known.
For example, let’s say you are given a circle with a circumference of 12 units. Plugging this value into the formula, you can calculate the radius as follows: r = 12 / 2π ≈ 12 / 6.28 ≈ 1.91 units. Therefore, the radius of the circle is approximately 1.91 units.
This quick calculation method can save you time and effort when you need to find the radius from the circumference of a circle. It is a handy tool to have in your mathematical toolkit and can be applied to various real-life scenarios where circle calculations are involved.
Key Takeaways and Final Thoughts
In this practice session on circles and circumference, we reviewed several word problems and their solutions. Through these problems, we practiced applying the formulas for circumference and area of circles, as well as using our knowledge of proportionality and algebraic equations.
The main takeaways from this practice session are:
- The formula for the circumference of a circle is C = 2πr, where C represents the circumference and r represents the radius.
- The formula for the area of a circle is A = πr^2, where A represents the area and r represents the radius.
- When solving word problems involving circles, it is important to understand the given information, identify the unknowns, and set up appropriate equations.
- Proportionality can be used to solve problems involving similar shapes, such as finding the radius or circumference of a larger or smaller circle.
- Using algebraic equations, we can solve for the unknown variables and find the values needed to answer the word problems.
Overall, this practice session has improved our understanding of circles and circumference, as well as our problem-solving skills. By applying these concepts in various word problems, we have developed a solid foundation for further studies in geometry and applied mathematics.