
Secant lines and segments are essential concepts in geometry. They help us understand the relationship between circles, tangents, and angles. To deepen your understanding of these concepts, we have provided 10 additional practice problems along with their answers. This article will walk you through each problem, explaining the steps to solve them and providing detailed explanations.
Each practice problem in this article focuses on a different aspect of secant lines and segments. You will encounter questions that involve finding the length of a secant segment, determining the measure of an angle formed by a secant and tangent, and solving for the missing side of a triangle formed by a secant line and tangent. By working through these problems, you will sharpen your skills in geometry and be better prepared for exams or future math challenges.
As you tackle each problem, it is important to approach them systematically. Remember to identify the given information, determine the desired quantity to find, and apply the appropriate formulas or theorems. Take your time and carefully analyze each problem, making sure to show all your work and calculations. If you encounter any difficulties, refer to the included answers for guidance and clarification.
By practicing these additional problems, you will reinforce your knowledge of secant lines and segments and build confidence in your geometric problem-solving abilities. So, let’s dive into the problems, explore the solutions, and enhance your understanding of this important topic in geometry!
5 Additional Practice Secant Lines and Segments Answers
In mathematics, secant lines and segments are important concepts that are used in geometry and trigonometry. They allow us to calculate different measurements and angles within a circle.
Here are 5 additional practice questions on secant lines and segments, along with their corresponding answers:
- Question: Find the length of a secant segment if the external part is 6 units long and the segment intersects the circle at two points that are 3 units apart on the circle’s circumference.
- Question: Given a circle with a radius of 5 units and a secant with an external part of 8 units, find the length of the secant segment.
- Question: Two secants intersect outside a circle. If the measure of the external angle between the two secants is 60 degrees, what is the measure of the intercepted arc between the two secants?
- Question: Given a circle with a radius of 7 units and a secant that intersects the circle at points A and B. If the length of segment AB is 10 units, what is the length of the tangent line drawn from the center of the circle to point B?
- Question: In a circle, a secant and a tangent intersect at a point outside the circle. If the length of the secant is 8 units and the distance from the point of intersection to the center of the circle is 5 units, what is the length of the segment of the tangent that is inside the circle?
Answer: To find the length of the secant segment, we can use the theorem of intersecting secants, which states that the product of the external part and the total secant segment is equal to the product of the external part and the other external part. In this case, 6 * x = 3 * 9 (since the external part and the other external part are equal, and the length of the secant segment is 9 units).
Answer: In this case, to find the length of the secant segment, we can use the Pythagorean theorem. The length of the secant segment squared is equal to the product of the external part and the sum of the external part and the entire secant. Substituting the given values, we get x^2 = 8 * (8 + 2*5) = 8 * 18. Solving for x, we find that the length of the secant segment is the square root of 144, which is 12 units.
Answer: The measure of the intercepted arc is equal to half the measure of the external angle. Therefore, the measure of the intercepted arc is 30 degrees.
Answer: To find the length of the tangent line, we can use the Pythagorean theorem. The length of the tangent line squared is equal to the difference between the square of the radius and the square of the segment AB. Substituting the given values, we get x^2 = 7^2 – 10^2 = 49 – 100 = -51. Since we can’t have a negative length, this means that there is no tangent line from the center of the circle to point B.
Answer: To find the length of the segment of the tangent inside the circle, we can use the theorem of intersecting tangents and secants, which states that the product of the length of the secant and the length of the entire tangent is equal to the square of the length of the distance from the point of intersection to the center of the circle. In this case, 8 * x = 5^2 = 25. Solving for x, we find that the length of the segment of the tangent inside the circle is 25/8 units.
These practice questions and their answers demonstrate the application of secant lines and segments in various geometric situations and highlight the importance of understanding these concepts in solving problems related to circles.
Understanding Secant Lines and Segments
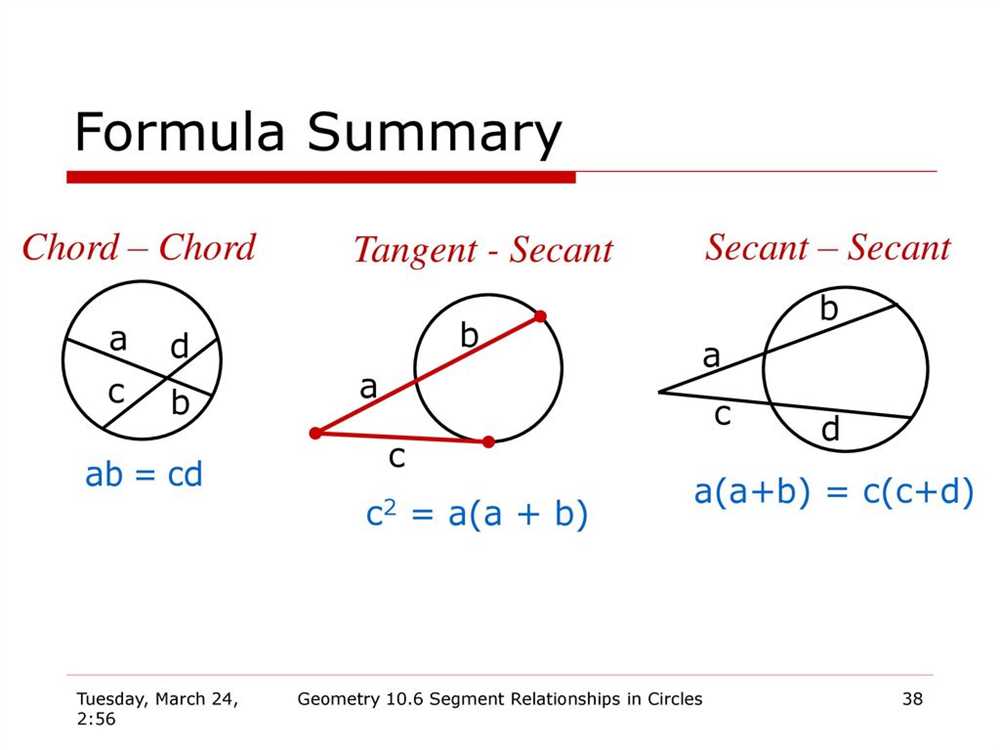
Secant lines and segments are important concepts in geometry that help us understand the relationship between a curve or circle and a line. A secant line is a line that intersects a curve or circle at two distinct points. On the other hand, a secant segment is a line segment with one endpoint on a curve or circle and the other endpoint outside of it.
Secant lines and segments can be used to find various properties of curves and circles. They are particularly useful in determining the slope of a curve at a specific point, as the slope of the secant line passing through the point approaches the slope of the curve itself as the two points of intersection get closer together. This concept is known as the secant line approximation.
In addition, secant lines and segments can also be used to find the length of an arc on a circle. By measuring the length of the secant segment and the angle formed by the two radii connecting the endpoints of the segment to the center of the circle, the length of the arc can be calculated using the following formula:
Arc length = Radius × Central angle (in radians)
Secant lines and segments are fundamental tools in the study of geometry, and they can be applied to various real-life situations such as navigation, engineering, and architecture. Understanding their properties and applications can greatly enhance our understanding and problem-solving abilities in the field of mathematics.
Definition of Secant Lines and Segments
A secant line is a line that intersects a circle at two distinct points. It can be thought of as a line that cuts through the circle. One of the key properties of secant lines is that they always have two points of intersection with the circle, unlike a tangent line which only has one point of intersection.
A secant segment is the part of a secant line that lies between the two points of intersection with the circle. It can be measured and compared to other secant segments or other segments within the circle. Secant segments play an important role in various geometric calculations and proofs.
In terms of circle geometry, secant lines and segments help establish relationships between angles, lengths, and other geometric properties within the circle. They are fundamental concepts that are used in various branches of mathematics, including trigonometry and calculus.
Understanding secant lines and segments is important for solving problems involving circles, including finding the lengths of tangent lines, determining the measures of angles formed by intersecting lines and circles, and analyzing the properties of arcs and chords within a circle.
Overall, secant lines and segments are fundamental concepts in circle geometry that are used to establish relationships and solve problems related to circles. They provide a way to connect different points on the circle and analyze their properties, making them an essential tool in geometric calculations and proofs.
Finding the Length of a Secant Segment
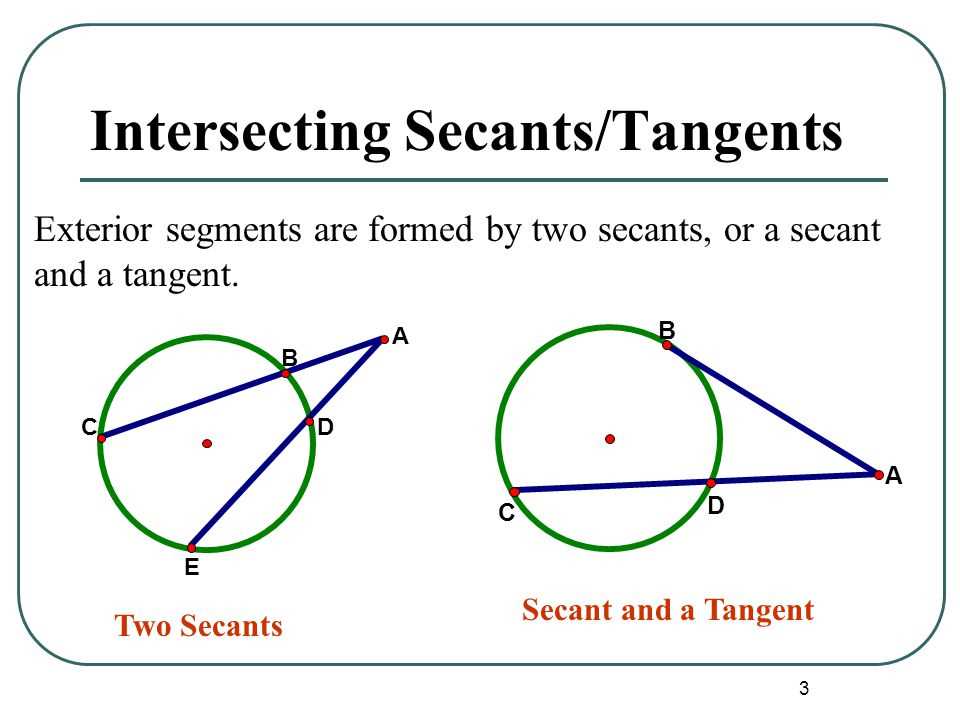
In geometry, a secant line is a line that intersects a circle at two different points. A secant segment is the part of the secant line that lies between the two points of intersection. Finding the length of a secant segment is an important skill in geometry, as it allows us to determine distances and solve various problems involving circles.
To find the length of a secant segment, we can use the formula: length of secant segment = (radius of the circle) * (secant’s intersected portion). The intersected portion is the part of the secant segment that lies inside the circle. This formula is derived from the relationship between the radius, secant, and tangent lines to a circle.
Before using the formula, it is crucial to accurately identify the radius of the circle and the length of the intersected portion of the secant line. Once these values are determined, we can plug them into the formula to calculate the length of the secant segment.
It’s important to note that secant segments can have two different lengths if the secant line intersects the circle both internally and externally. In such cases, we need to consider both lengths separately by using the formula for each intersected portion.
Knowing how to find the length of a secant segment is essential for various applications, such as determining the distance between two points on a circle or finding the length of a line segment that intersects a circle. Practice and understanding the formula will help you confidently solve problems involving secant lines and segments in geometry.
Calculating the Slope of a Secant Line
A secant line is a straight line that intersects a curve at two or more points. When studying calculus and analyzing the behavior of functions, it is often necessary to calculate the slope of a secant line. The slope of a secant line represents the average rate of change of the function over a specific interval.
To calculate the slope of a secant line, you need to determine the change in the function’s output (y-values) divided by the change in the input (x-values). This can be expressed as the difference quotient formula: (f(x2) – f(x1)) / (x2 – x1). Here, f(x2) and f(x1) represent the function values at the corresponding x-values x2 and x1.
For example, let’s say we have a function f(x) = x^2 and we want to calculate the slope of the secant line between the points (1, 1) and (3, 9). Using the difference quotient formula, we can find that the slope is (9 – 1) / (3 – 1) = 4.
Calculating the slope of a secant line can provide valuable insights into the behavior of a function. It allows us to approximate the instantaneous rate of change at a specific point and understand how the function is changing over a given interval. By analyzing the slopes of secant lines, we can gain a deeper understanding of the function’s concavity, increasing or decreasing behavior, and direction of change.
Identifying Secant Lines in a Graph
A secant line is a line that intersects a curve at two or more points. In the context of a graph, it represents the line that passes through two points on the graph, connecting them. It is essential to be able to identify these secant lines to analyze the behavior of the graph and understand its properties.
One way to find secant lines in a graph is by selecting two distinct points on the curve and drawing a straight line that passes through them. These points should not be too close to each other, as that would make the secant line almost indistinguishable from a tangent line. By connecting the two points with a line, you can observe the slope of the secant line and determine how it relates to the graph’s overall shape.
To identify secant lines, it is crucial to compare their slopes with those of tangent lines. Tangent lines represent the instantaneous rate of change at a specific point on the curve. Unlike tangent lines, secant lines give a broader view of the graph’s behavior between two points.
By examining the slopes of different secant lines at various points on a graph, you can gain insights into the graph’s concavity, the presence of maximum or minimum points, and the overall trend of the function. Secant lines can help you understand the rate of change and how it varies across different sections of the graph.
In summary, identifying secant lines in a graph allows us to analyze the overall behavior, slope, and rate of change of the function represented by the graph. By comparing secant lines with tangent lines, we can gain a deeper understanding of the graph’s properties and make more informed interpretations.
Solving Problems Involving Secant Lines and Segments
When dealing with secant lines and segments, it is important to have a strong understanding of their properties and how they relate to other geometrical elements. By solving problems involving secant lines and segments, we can further enhance our geometric reasoning and problem-solving skills.
One common problem involves finding the length of a secant segment. To solve this problem, we can use the intersecting chord theorem, which states that if a chord intersects with a secant line or another chord, the products of the lengths of the segments of the chord are equal. By setting up an equation using this theorem, we can determine the length of the desired secant segment. This problem-solving approach can be applied to various situations where we need to find the length of a secant segment.
Another problem-solving scenario involves finding the distance between a point and a secant line. In this case, we can use the perpendicular bisector theorem, which states that if a line is perpendicular to a chord and passes through its midpoint, it is the perpendicular bisector of the chord. By drawing a perpendicular line from the point to the secant line and using this theorem, we can determine the distance between the point and the secant line. This problem-solving technique is useful in situations where we need to find the shortest distance between a point and a secant line.
In summary, solving problems involving secant lines and segments requires a deep understanding of their properties and the use of relevant theorems. By employing these problem-solving techniques, we can enhance our geometrical reasoning and develop a stronger grasp of secant lines and segments.