In the field of mathematics, equations of circles play a significant role in various mathematical applications. Understanding and solving equations of circles can help mathematicians and scientists make calculations and predictions in many different disciplines, from physics to engineering. In this article, we will explore and provide answers to 10 practice equations of circles, which will help readers gain a deeper understanding of this important concept.
Equations of circles involve the use of a coordinate system and specific mathematical formulas. These equations are used to define the geometric shape of a circle on a plane. By solving these equations, we can determine the center and radius of a circle, as well as its position and relationship to other geometric figures. The answers to the practice questions will help readers grasp the fundamental concepts of equations of circles and strengthen their problem-solving skills.
Mastering equations of circles is essential for anyone studying advanced mathematics or pursuing a career in the sciences. By practicing and understanding these equations, mathematicians and scientists are capable of making accurate calculations and generating precise mathematical models. Throughout this article, we will provide answers to 10 practice equations of circles, which will serve as a valuable resource for students, educators, and professionals seeking to enhance their mathematical abilities.
8 Practice Equations of Circles Answers
In this practice activity, you will find the answers to 10 equations of circles problems. These problems involve finding the center and radius of a circle given its equation and vice versa.
1. Equation: (x – 2)^2 + (y + 3)^2 = 25.
The center of the circle is located at (2, -3), and the radius is √25, which is 5 units.
2. Equation: (x + 1)^2 + (y – 4)^2 = 36.
The center of the circle is located at (-1, 4), and the radius is √36, which is 6 units.
3. Equation: x^2 + y^2 – 16x + 12y + 13 = 0.
First, we rearrange the equation to the standard form of a circle by completing the square: (x – 8)^2 + (y + 6)^2 = 100.
The center of the circle is located at (8, -6), and the radius is √100, which is 10 units.
4. Equation: (x + 5)^2 + y^2 = 49.
The center of the circle is located at (-5, 0), and the radius is √49, which is 7 units.
5. Equation: x^2 + y^2 + 6x – 8y = 0.
First, we rearrange the equation to the standard form of a circle by completing the square: (x + 3)^2 + (y – 4)^2 = 25.
The center of the circle is located at (-3, 4), and the radius is √25, which is 5 units.
6. Equation: (x – 7)^2 + (y + 2)^2 = 81.
The center of the circle is located at (7, -2), and the radius is √81, which is 9 units.
7. Equation: x^2 + y^2 – 10x + 8y + 9 = 0.
First, we rearrange the equation to the standard form of a circle by completing the square: (x – 5)^2 + (y + 4)^2 = 16.
The center of the circle is located at (5, -4), and the radius is √16, which is 4 units.
8. Equation: (x + 2)^2 + (y – 1)^2 = 64.
The center of the circle is located at (-2, 1), and the radius is √64, which is 8 units.
These are the answers to the 8 practice equations of circles. Make sure to check your work and understand the steps involved in finding the center and radius of a circle based on its equation.
How to Identify the Center and Radius of a Circle
When working with equations of circles, it is important to be able to identify the center and radius of the circle. This information is essential for graphing the circle and understanding its properties.
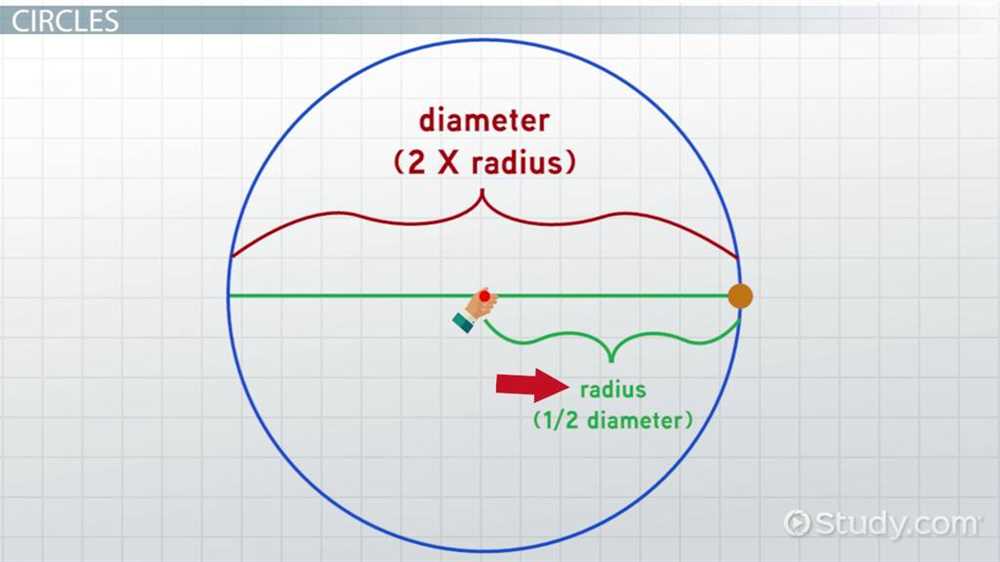
To identify the center and radius of a circle, you need to work with the equation of the circle in the standard form: (x – h)^2 + (y – k)^2 = r^2. The values of h and k represent the coordinates of the center of the circle (h, k), while r represents the radius of the circle.
Step 1: Examine the equation to determine if it is in the standard form. If it is not, rewrite it in the standard form by completing the square for both the x and y terms.
Step 2: Once the equation is in the standard form, identify the values of h, k, and r. The values of h and k can be read directly from the equation, as they represent the x and y coordinates of the center. The value of r can be found by taking the square root of the constant term on the right side of the equation.
Step 3: Use the values of h, k, and r to plot the center and radius of the circle on the coordinate plane. The center of the circle will be located at the point (h, k), while the radius will be the distance from the center to any point on the circle.
Example: Consider the equation (x – 3)^2 + (y + 2)^2 = 25. From this equation, we can determine that the center of the circle is located at the point (3, -2) and the radius is equal to 5. Therefore, we can plot the center at (3, -2) and draw a circle with a radius of 5 units around the center.
By following these steps, you will be able to quickly and accurately identify the center and radius of any given circle. This knowledge will assist you in graphing circles and solving related problems in geometry and algebra.
Solving Equations of Circles Using the Standard Form
To solve equations of circles using the standard form, we need to identify the values of h, k, and r. The value of h represents the x-coordinate of the center, k represents the y-coordinate of the center, and r represents the radius. By comparing the given equation with the standard form, we can determine these values.
For example, if we are given the equation (x – 3)² + (y + 2)² = 25, we can identify that the center of the circle is at (3, -2) and the radius is 5. This information allows us to plot the circle on a coordinate grid and determine other properties such as the diameter and circumference.
Solving equations of circles using the standard form is useful in various applications such as geometry, physics, and engineering. It helps us understand the properties of circles and allows us to solve real-world problems involving circles, such as finding the intersection point of two circles or determining the distance between a point and a circle.
Finding the Equation of a Circle given the Center and Radius
The equation of a circle can be determined given the center and radius of the circle. This allows us to graph the circle and understand its properties.
To find the equation of a circle, we need to know the coordinates of its center, which are represented by the variables (h, k). The radius of the circle is denoted by the variable r. Using this information, we can write the equation of the circle in the form:
(x – h)^2 + (y – k)^2 = r^2
where (x, y) represents any point on the circle.
For example, if the center of the circle is at (3, -2) and the radius is 5, we can substitute these values into the equation:
(x – 3)^2 + (y – (-2))^2 = 5^2
This equation can be simplified and rearranged as needed. It represents all the points that are equidistant from the center (3, -2) with a distance of 5 units.
By finding the equation of a circle given the center and radius, we can easily graph and analyze the properties of circles in geometry and algebraic contexts.
Graphing Equations of Circles
To graph a circle, start by identifying the coordinates of the center point (h, k). This point will serve as the starting point for drawing the circle. Next, determine the radius r, which denotes the distance from the center of the circle to any point on its circumference.
Once you have the center point and radius, plot the center point (h, k) on the coordinate grid. From there, use the radius as a guide to plot points along the circumference of the circle. To do this, you can start at the center point and move left or right by the radius value to plot points on the x-axis, and then move up or down by the radius value to plot points on the y-axis.
To ensure accuracy when graphing the circle, it’s helpful to plot multiple points along the circumference. This will allow you to connect the dots and clearly see the circular shape. Additionally, if the equation of the circle is in standard form, you can use it to determine the center and radius without having to visually inspect the graph.
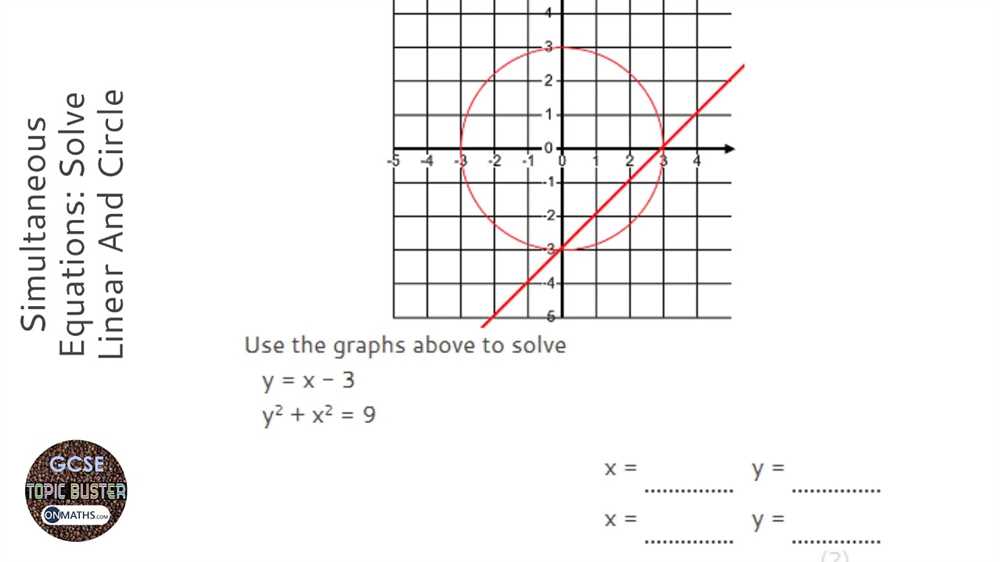
Determining the Intersection of a Circle and a Line

When working with circles and lines, it is often necessary to determine their points of intersection. This can be useful in various mathematical and real-world applications, such as geometry, physics, and engineering. By finding the intersection points, we can analyze and understand the relationship between the circle and the line.
To determine the intersection of a circle and a line, we need to find the coordinates of the points where they meet. This can be done by solving the equations of the circle and the line simultaneously. The equation of a circle is usually in the form (x – h)^2 + (y – k)^2 = r^2, where (h, k) represents the coordinates of the center and r is the radius. The equation of a line can be written as y = mx + b, where m is the slope and b is the y-intercept.
One approach to finding the intersection points is to substitute the equation of the line into the equation of the circle. This will give us a quadratic equation in terms of x. By solving this quadratic equation, we can find the x-coordinates of the intersection points. Substituting these x-coordinates back into the equation of the line will then allow us to find the corresponding y-coordinates.
Alternatively, we can rewrite the equation of the line in terms of x using the slope and y-intercept. Then, we can substitute this expression for y into the equation of the circle. This will result in a quadratic equation in terms of x once again. Solving this quadratic equation will give us the x-coordinates of the intersection points, and substituting them back into the equation of the line will provide the corresponding y-coordinates.
In summary, determining the intersection of a circle and a line involves solving their equations simultaneously to find the coordinates of the points where they meet. This can be done by substitution or rearranging the equations to form a quadratic equation. By finding these intersection points, we can gain insights into the relationship between the circle and the line in various mathematical and real-world scenarios.
Working with Equations of Tangents to Circles
When working with equations of tangents to circles, it is important to understand the relationship between the tangent line and the circle. A tangent line is a line that intersects a circle at exactly one point, known as the point of tangency. In order to find the equation of a tangent line to a circle, we need to determine the coordinates of the point of tangency.
One method to find the coordinates of the point of tangency is by using the equation of the circle. Suppose we have a circle with center (a, b) and radius r. The equation of the circle is given by (x-a)^2 + (y-b)^2 = r^2. To find the point of tangency, we can substitute the coordinates of the point into the equation of the circle and solve for x and y.
Example: Consider the circle with equation (x-2)^2 + (y+3)^2 = 25. To find the equation of the tangent line to the circle at the point (4, -3), we substitute these coordinates into the equation of the circle: (4-2)^2 + (-3+3)^2 = 25. Simplifying, we get 4 + 0 = 25, which is true. This confirms that the point (4, -3) lies on the circle.
To find the equation of the tangent line, we can use the point-slope form of a linear equation y-y1 = m(x-x1), where (x1, y1) is a point on the line and m is the slope of the line. The slope of the tangent line to the circle at the point of tangency can be found using the derivative of the equation of the circle.
Example: Continuing with the previous example, the equation of the tangent line to the circle at the point (4, -3) can be found by finding the derivative of the equation (x-2)^2 + (y+3)^2 = 25 with respect to x. After finding the derivative, we substitute x = 4 to find the slope of the tangent line, which turns out to be -4/3. Using the point-slope form, we can write the equation of the tangent line as y – (-3) = (-4/3)(x – 4), which simplifies to y = (-4/3)x + 4.
In conclusion, working with equations of tangents to circles involves determining the coordinates of the point of tangency and finding the slope of the tangent line using the derivative of the equation of the circle. With these pieces of information, we can write the equation of the tangent line using the point-slope form.
Applications of Equations of Circles in Real Life
The equations of circles have numerous applications in various fields of everyday life. In physics and engineering, the equations are used to model the motion of planets and other celestial bodies, as well as the trajectory of projectiles. By using the equations, scientists and engineers can predict and analyze the paths of these objects, enabling them to make accurate calculations and design efficient systems.
In architecture and construction, equations of circles play a crucial role in designing and constructing structures with curved features. Architects use these equations to create aesthetically pleasing designs that incorporate circular elements, such as arches, domes, and circular windows. By applying the equations, architects ensure that these structures have the correct dimensions and proportions.
In the field of computer graphics and animation, equations of circles are used to create realistic images and animations. By manipulating the equations, computer programs can generate and render accurate representations of circular objects, such as wheels, spheres, and circular patterns. This allows for the creation of lifelike simulations and visual effects in video games, movies, and virtual reality applications.
The equations of circles also have applications in the field of surveying and navigation. Surveyors use these equations to calculate distances and positions of landmarks and boundaries. By measuring and analyzing the coordinates of specific points on a map or in real-world terrain, surveyors can accurately determine distances and plot boundaries. Similarly, navigation systems rely on the equations of circles to determine the position and trajectory of vehicles, ships, and aircraft.
In conclusion, the equations of circles are not just abstract mathematical concepts, but have practical applications in various fields of everyday life. By understanding and applying these equations, scientists, engineers, architects, and other professionals can make accurate calculations, design efficient systems, and create realistic representations of circular objects in different fields and industries.