In mathematics, logarithms are an important tool for solving equations that involve exponentials. Logarithmic functions are the inverse of exponential functions, and they can be graphed to help visualize the relationship between the input and output values.
When graphing logarithmic functions, it is essential to understand the key properties that dictate their shape. These properties include the domain, range, vertical asymptote, and horizontal asymptote. By analyzing these characteristics, we can accurately sketch the graph of a logarithmic function.
The answer key for graphing logarithmic functions provides a step-by-step guide to finding these properties and drawing the graph. It offers a comprehensive solution to common problems encountered while graphing logarithmic functions, including finding the x-intercepts and y-intercepts, determining the direction of the graph, and identifying any transformations or reflections.
By using the answer key for graphing logarithmic functions, students and educators can gain a deeper understanding of these functions and develop their proficiency in graphing them accurately. This guide serves as a valuable resource, providing clear explanations and examples to assist in solving logarithmic function graphing problems.
What Are Logarithms?
A logarithm is a mathematical function that helps solve exponential equations by converting them into simpler forms. It is the inverse operation of exponentiation, just like division is the inverse of multiplication. Logarithms are widely used in various fields, including mathematics, science, finance, and computer science, to simplify calculations and analyze data.
The logarithm of a number tells you the exponent to which another fixed number, called the base, must be raised to obtain that number. In other words, if y = logb(x), then x = by. The most commonly used logarithms are the natural logarithm (base e) and the common logarithm (base 10), denoted as ln and log, respectively.
Logarithms have many useful properties that make them valuable in problem-solving. For example, logarithms allow us to simplify complex equations involving exponents, transform multiplication into addition, and division into subtraction. They also help convert large numbers into more manageable forms and compare the relative sizes of different quantities.
Logarithmic functions are often used to model various phenomena in science and engineering, such as population growth, radioactive decay, and sound intensity. They can also be applied in finance to calculate interest rates, in computer science for algorithm analysis, and in data analysis to measure the spread of information.
In summary, logarithms are powerful mathematical tools that enable us to solve exponential equations, simplify calculations, and analyze data in various fields. Understanding logarithms is essential for anyone studying advanced mathematics and working with complex relationships and quantitative information.
Understanding Exponential Functions
An exponential function is a mathematical function that represents the growth or decay of a quantity at a constant relative rate. Exponential functions have the general form f(x) = ab^x, where a is the initial value, b is the base, and x is the exponent.
Exponential functions are characterized by their rapid growth or decay. When the base (b) is greater than 1, the function experiences exponential growth, where the output values increase rapidly as the input values increase. On the other hand, when the base is between 0 and 1, the function undergoes exponential decay, where the output values decrease rapidly as the input values increase.
Example:
To illustrate the concept of exponential functions, let’s consider an example where the initial value (a) is 5 and the base (b) is 2. The function can be written as f(x) = 5 * 2^x.
If we substitute different values of x into the function, we can observe the corresponding output values. For example, when x = 0, f(0) = 5 * 2^0 = 5 * 1 = 5. When x = 1, f(1) = 5 * 2^1 = 5 * 2 = 10. And so on.
We can see that as x increases, the output values of the function increase rapidly due to the exponential growth. This characteristic makes exponential functions useful in modeling various real-world phenomena, such as population growth, compound interest, and radioactive decay.
In summary, exponential functions provide a powerful tool for understanding and predicting the growth or decay of quantities at a constant relative rate. By manipulating the initial value and base, we can model a wide range of natural and mathematical phenomena.
Definition of Exponential Functions
An exponential function is a mathematical function in the form of f(x) = a^x, where a is a positive constant called the base and x is the independent variable. The exponential function is a fundamental concept in mathematics and has various applications in science, finance, and engineering.
Exponential functions exhibit a specific pattern of growth or decay, known as exponential growth or exponential decay, respectively. In exponential growth, the function increases rapidly as the value of x increases, while in exponential decay, the function decreases rapidly as the value of x increases. The base a determines the rate of growth or decay of the function.
Exponential functions have several important properties. One of the key properties is that the range of exponential functions is always positive, meaning that the output values are greater than zero. This is because raising a positive number to any power always results in a positive number. Additionally, exponential functions are continuous and smooth, meaning that there are no abrupt changes or discontinuities in the graph.
The graph of an exponential function will either be an increasing curve or a decreasing curve, depending on the value of the base. If the base a is greater than 1, the function will exhibit exponential growth and the graph will be an upward curve. On the other hand, if the base a is between 0 and 1, the function will exhibit exponential decay and the graph will be a downward curve.
Exponential functions are commonly used to model various real-world phenomena, such as population growth, radioactive decay, compound interest, and the spread of diseases. They provide a mathematical framework for understanding and predicting the behavior of quantities that grow or decay exponentially over time.
Properties of Exponential Functions
Exponential functions are a type of mathematical function that involves raising a base number to a variable exponent. They have several unique properties that make them important in various fields of mathematics and real-world applications.
- Exponential Growth or Decay: An exponential function can exhibit either exponential growth or exponential decay, depending on the value of the base. If the base is greater than 1, the function will exhibit exponential growth, whereas if the base is between 0 and 1, the function will exhibit exponential decay.
- Constant Ratio: Exponential functions have a constant ratio between successive outputs, which means that for every increase in the input, the output will increase or decrease by a fixed factor.
- Asymptotes: Exponential functions often have horizontal asymptotes at y=0 or vertical asymptotes at x=0, depending on the properties of the function.
- Positive or Negative: Exponential functions can be positive or negative, depending on the value of the base and the exponent.
- Domain and Range: The domain of an exponential function is all real numbers, while the range depends on the properties of the function.
Exponential functions have numerous applications in fields such as finance, population growth, radioactive decay, and compound interest. They can help describe and analyze exponential growth or decay processes, predict future values based on current data, and model various natural phenomena. Understanding the properties of exponential functions is essential for solving problems and making accurate predictions in these areas.
Definition of Logarithmic Functions
A logarithmic function is a mathematical function that represents the inverse of an exponential function. It can be written in the form: y = logb(x), where ‘y’ is the logarithm of ‘x’ with base ‘b’. The logarithm of a number is the exponent to which the base must be raised to obtain that number.
The logarithmic function can be graphed on a coordinate plane, where the x-axis represents the input values and the y-axis represents the corresponding logarithmic values. The graph of a logarithmic function generally takes the shape of a curve that approaches the x-axis but never touches it.
The base of the logarithmic function determines the properties of the graph. If the base is greater than 1, the logarithmic function is increasing. This means that as the input values increase, the corresponding logarithmic values also increase. On the other hand, if the base is between 0 and 1, the logarithmic function is decreasing, which means that as the input values increase, the corresponding logarithmic values decrease.
Logarithmic functions have several important properties that make them useful in various areas of mathematics and science. They can be used to solve exponential equations, find the inverse of exponential functions, model population growth, measure the intensity of earthquakes, and more. Understanding logarithmic functions and their graphs is essential for understanding exponential growth and decay phenomena.
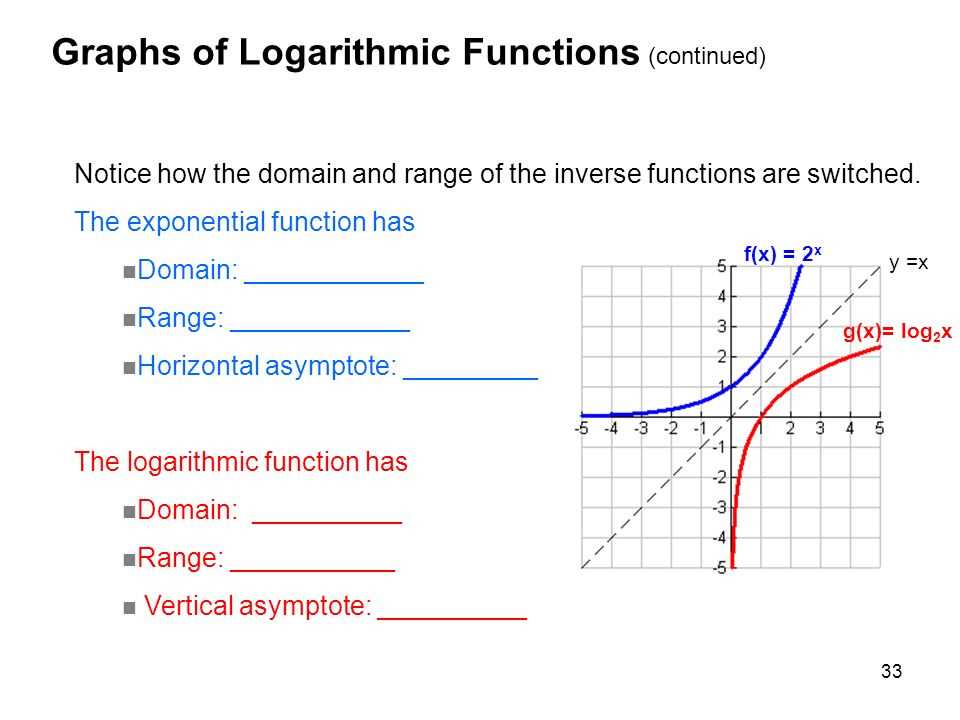
Relationship between Exponential and Logarithmic Functions
Exponential and logarithmic functions are two types of mathematical functions that are closely related to each other. They are inverse functions of each other, meaning that they undo each other’s operations.
An exponential function is a function in the form of y = a^x, where a is the base and x is the exponent. This function represents exponential growth or decay. As x increases, the value of y grows at an increasing rate.
A logarithmic function, on the other hand, is the inverse of an exponential function. It is written in the form of y = log_a(x), where a is the base, x is the argument, and y is the exponent. The logarithmic function calculates the power to which the base must be raised to obtain the argument.
In simpler terms, an exponential function represents the growth or decay of a quantity over time, while a logarithmic function helps us determine the exponent needed to obtain a given value. They are like two sides of the same coin, providing information about different aspects of a mathematical relationship.
The relationship between exponential and logarithmic functions can be further understood by examining their graphs. An exponential function has a graph that starts at the y-intercept and grows or decays rapidly as x increases or decreases. A logarithmic function, on the other hand, has a graph that starts at the x-intercept and grows slowly as x increases.
Understanding the relationship between exponential and logarithmic functions is important in various fields, such as finance, biology, and computer science. Exponential functions can be used to model population growth, compound interest, and exponential decay. Logarithmic functions are used in solving exponential equations, finding the time complexity of algorithms, and analyzing data in a logarithmic scale.
In conclusion, exponential and logarithmic functions are inverse functions that are closely related. They provide information about the growth, decay, and relationships between quantities. Understanding their relationship is crucial in various fields and helps in solving complex mathematical problems.
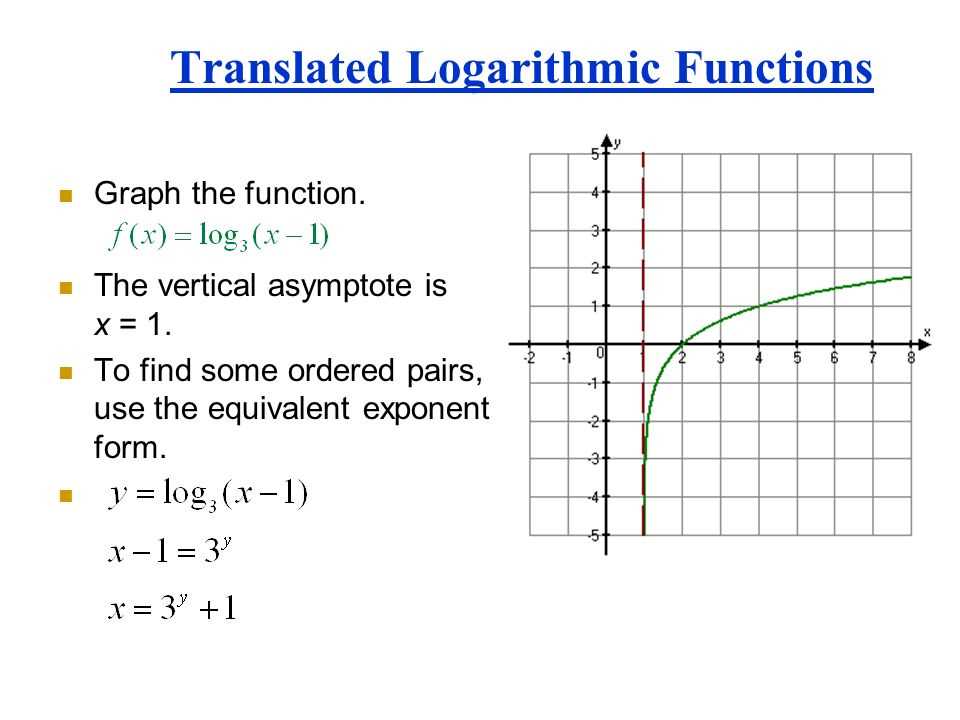
Graphing Logarithmic Functions
A logarithmic function is the inverse operation of an exponential function. It is represented by the formula y = log_base(x), where y is the logarithm of x with respect to a specified base. Logarithmic functions are commonly used in mathematics, physics, and engineering to describe exponential growth or decay.
When graphing logarithmic functions, it is important to understand the properties of the function and how they affect the shape of the graph. The graph of a logarithmic function typically exhibits a few key characteristics:
- The domain of a logarithmic function is all positive real numbers, as the logarithm of zero or a negative number is undefined.
- The range of a logarithmic function is all real numbers, as the logarithm of any positive number is defined.
- The graph of a logarithmic function approaches but never reaches the x-axis.
- The graph of a logarithmic function is symmetric with respect to the vertical line x = 1, as any value raised to the power of 1 is equal to itself.
When graphing logarithmic functions, it is helpful to identify key points on the graph, such as the intercepts, asymptotes, and any vertical or horizontal shifts. The base of the logarithmic function also plays a role in determining the shape of the graph. A logarithmic function with a base greater than 1 will exhibit exponential growth, while a base between 0 and 1 will exhibit exponential decay.
In summary, graphing logarithmic functions involves understanding their properties and using that knowledge to accurately plot their graphs. By identifying key points and considering the base of the function, one can create an accurate representation of a logarithmic function on a graph.
Understanding Logarithmic Graphs
A logarithmic graph represents the relationship between two variables, where one variable is plotted on a logarithmic scale. The logarithmic scale allows for a wide range of values to be represented on a graph, making it particularly useful in cases where the data spans several orders of magnitude.
When graphing a logarithmic function, it is important to consider the shape of the graph. A logarithmic graph will have a distinct curve, with the curve becoming steeper as the values on the x-axis increase. This means that as the input variable increases, the corresponding output variable increases at a decreasing rate.
For example, let’s consider the graph of the logarithmic function y = log(x). As x approaches infinity, the value of log(x) approaches infinity, but at a decreasing rate. Similarly, as x approaches zero, the value of log(x) approaches negative infinity, also at a decreasing rate. The graph of this function would have a curve that starts steeply and gradually flattens as x increases.
Another important feature of logarithmic graphs is the presence of an asymptote. An asymptote is a line that the graph approaches but does not intersect. For logarithmic functions, the vertical line x = 0 is always an asymptote. This means that the graph will get indefinitely close to the line x = 0, but will never touch or cross it.
Understanding the characteristics of logarithmic graphs is essential for interpreting data and making predictions based on the relationship between the variables. By analyzing the curve, steepness, and presence of asymptotes, we can gain valuable insights into the behavior of the variables and make informed decisions in various fields such as economics, biology, and engineering.