
Polynomial expressions are a fundamental concept in algebra and mathematics as a whole. They form the basis for solving equations, graphing functions, and understanding complex mathematical relationships. So, if you’re struggling to fully grasp the intricacies of polynomial expressions, fear not! In this article, we will delve into the answer key for 17-1 polynomial expressions, decoding its essential components and providing you with a comprehensive understanding of how to solve these problems like a pro.
When working with polynomial expressions, it’s essential to start by understanding the fundamentals. Polynomials consist of terms, each comprising variables raised to different powers and multiplied by coefficients. These terms can be combined through addition or subtraction to form the expression. The degree of a polynomial is determined by the highest power of the variable in any of its terms. To solve for the value of the expression, we substitute the given values into the expression and perform the necessary operations according to the order of operations.
Now, let’s dive into understanding the answer key for 17-1 polynomial expressions. This answer key provides step-by-step solutions to the problems presented in the exercise. It breaks down each question into smaller, more manageable parts, making it easier to comprehend and follow. By studying the answer key, you can gain insights into the reasoning behind each solution and learn valuable problem-solving techniques that can be applied to similar polynomial expressions.
Definition and Components of Polynomial Expressions
A polynomial expression is a mathematical expression that consists of variables, constants, and mathematical operations such as addition, subtraction, multiplication, and exponentiation. It is an essential concept in algebra and is used to represent a wide variety of mathematical equations and calculations.
A polynomial expression is made up of terms, which are individual components of the expression. Each term can be a constant, a variable, or a combination of both, and it is multiplied by a coefficient. The coefficient is a numerical value that determines the magnitude of the term. The terms in a polynomial expression are separated by addition or subtraction symbols.
The degree of a polynomial expression is determined by the highest exponent of the variable in the expression. For example, in the polynomial expression 3x^2 + 2x – 1, the highest exponent of x is 2, so the degree of the expression is 2. The degree of a polynomial expression provides information about the complexity and behavior of the polynomial.
Polynomial expressions can be classified based on their degree. A polynomial with a degree of 1 is called a linear polynomial, while a polynomial with a degree of 2 is called a quadratic polynomial. Polynomials with higher degrees, such as cubic, quartic, or quintic polynomials, have more complex forms and behaviors.
Polynomial expressions are widely used in various fields of mathematics, including algebra, calculus, and statistics. They are used to model real-world phenomena, solve equations, and make predictions. Understanding the components and properties of polynomial expressions is crucial for performing mathematical operations and interpreting mathematical equations.
Examples of Polynomial Expressions
Polynomial expressions are algebraic expressions that consist of variables, coefficients, and exponents. They can be comprised of one or more terms, which are separated by addition or subtraction operations. Here are a few examples of polynomial expressions:
Example 1: Monomial
A monomial is a polynomial expression with only one term. It can be represented as:
- 5x: This monomial consists of a coefficient (5) and a variable (x) raised to the power of 1. It represents the product of 5 and x.
Example 2: Binomial
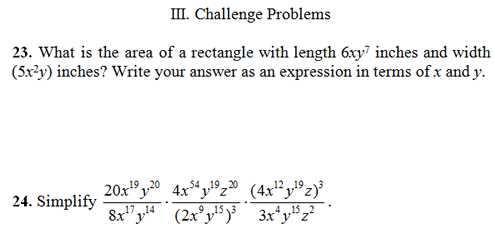
A binomial is a polynomial expression with two terms. It can be represented as:
- 3x + 2: This binomial consists of two terms, 3x and 2, separated by the addition operation. It represents the sum of 3x and 2.
Example 3: Trinomial

A trinomial is a polynomial expression with three terms. It can be represented as:
- 2x^2 – 4x + 1: This trinomial consists of three terms, 2x^2, -4x, and 1, separated by the subtraction and addition operations. It represents the difference of 2x^2 and 4x, and the sum of 1.
Example 4: Polynomial with more than three terms
A polynomial expression can also have more than three terms. For example:
- x^3 – 2x^2 + 3x – 4: This polynomial expression consists of four terms, x^3, -2x^2, 3x, and -4. It represents the difference of x^3 and 2x^2, the sum of 3x, and the difference of 4.
These are just a few examples of polynomial expressions. They can have different degrees and different arrangements of terms, but they all follow the basic structure of algebraic expressions with variables, coefficients, and exponents.
Understanding Polynomial Degree
A polynomial is an algebraic expression that consists of variables, coefficients, and exponents. The degree of a polynomial is determined by the highest power of the variable in the expression. It is a crucial concept in understanding and manipulating polynomial expressions.
The degree of a polynomial can help us determine important characteristics of the expression, such as its behavior, the number of solutions, and the potential complexity of solving the equation. Understanding the degree is essential for solving polynomial equations and simplifying expressions.
The degree of a polynomial is determined by examining the exponents of the variables. For example, in the polynomial expression 3x^2 + 2x – 5, the highest power of x is 2. Therefore, the degree of this polynomial is 2.
Polynomial expressions can have different degrees. A polynomial with a degree of 0 is considered a constant, as it does not contain any variables. A polynomial with a degree of 1 is known as a linear polynomial, while a polynomial with a degree of 2 is called a quadratic polynomial.
Higher-degree polynomials, such as cubic (degree 3), quartic (degree 4), and quintic (degree 5), introduce additional complexity in terms of their behavior and solutions. The degree of a polynomial can provide insights into its overall shape and behavior, including the presence of local minima and maxima, inflection points, and the behavior at the endpoints of the domain.
In summary, understanding the degree of a polynomial is crucial for analyzing and manipulating polynomial expressions. It allows us to determine important characteristics and behaviors of the expression, which can aid in solving equations and simplifying the overall expression.
Degree of a Polynomial
In mathematics, a polynomial is an expression consisting of variables (also known as indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. The degree of a polynomial is the highest power of the variable in that polynomial.
Degree of a Monomial
A monomial is a polynomial with only one term. The degree of a monomial is the sum of the exponents of its variables. For example, in the monomial 3x^2y^3, the degree is 2 + 3 = 5.
Degree of a Polynomial
A polynomial is a sum of monomials. The degree of a polynomial is determined by the degree of the monomial with the highest degree in the polynomial. For example, the polynomial 2x^3 + 5x^2 + 3x has a degree of 3, because the monomial with the highest degree is 2x^3.
Note that the degree of a polynomial can never be negative. If a polynomial has all zero coefficients, it is considered to have a degree of negative infinity.
The degree of a polynomial is an important property as it helps determine many characteristics of the polynomial, such as the number of solutions it has, its behavior as the variable approaches infinity or negative infinity, and its general shape on a graph.
Examples of Polynomial Degrees

Polynomials are algebraic expressions with one or more terms. The degree of a polynomial is determined by the highest power of the variable in the expression. Here are some examples of polynomials with different degrees:
Degree 0: A polynomial of degree 0 is a constant. It does not contain any variable. For example, the expression “5” is a polynomial of degree 0. It is a constant because it does not change.
Degree 1: A polynomial of degree 1 has only one term with a variable raised to the power of 1. For example, the expression “2x” is a polynomial of degree 1. It represents a linear equation because the variable x is raised to the power of 1.
Degree 2: A polynomial of degree 2 has one term with a variable raised to the power of 2. For example, the expression “3x^2 + 2x – 1” is a polynomial of degree 2. It represents a quadratic equation because the highest exponent of the variable is 2.
Degree 3: A polynomial of degree 3 has one term with a variable raised to the power of 3. For example, the expression “4x^3 + 3x^2 – 2x + 1” is a polynomial of degree 3. It represents a cubic equation because the highest exponent of the variable is 3.
Degree 4: A polynomial of degree 4 has one term with a variable raised to the power of 4. For example, the expression “5x^4 + 4x^3 – 3x^2 + 2x – 1” is a polynomial of degree 4. It represents a quartic equation because the highest exponent of the variable is 4.
Higher Degrees: Polynomials can have higher degrees as well. For example, a polynomial of degree 5 would have one term with a variable raised to the power of 5, and so on.
In summary, the degree of a polynomial determines the highest power of the variable in the expression. Different degrees of polynomials represent different types of equations, such as linear, quadratic, cubic, and quartic equations.
Operations with Polynomial Expressions

Polynomial expressions are mathematical expressions that consist of variables raised to different powers and combined using addition, subtraction, multiplication, and division operations. Understanding how to perform these operations is essential in solving polynomial equations and simplifying expressions.
Addition and Subtraction: When adding or subtracting polynomial expressions, it is important to combine like terms. Like terms are terms that have the same variable raised to the same power. To add or subtract like terms, simply add or subtract the coefficients while keeping the variables and exponents unchanged. For example, to add 2x^2 + 3x – 5 with 4x^2 – 2x + 1, combine the like terms to get 6x^2 + x – 4.
Multiplication: When multiplying polynomial expressions, you need to use the distributive property. Multiply each term of one polynomial by every term of the other polynomial, and then combine like terms if possible. For example, to multiply (2x – 3)(x + 4), you would use the distributive property to get 2x^2 + 5x – 12.
Division: Dividing polynomial expressions involves long division or synthetic division. Long division is similar to division of whole numbers, but you divide terms instead of digits. Synthetic division is a shorthand method used specifically for dividing by binomials of the form (x – a). Both methods allow you to simplify or factorize polynomial expressions into simpler forms.
In summary, mastering the operations with polynomial expressions is crucial in algebraic manipulations, solving equations, and understanding the behavior of quadratic, cubic, and higher degree polynomial functions.
Addition and Subtraction of Polynomial Expressions
When working with polynomial expressions, it is often necessary to add or subtract them in order to simplify or solve equations. Adding and subtracting polynomial expressions involves combining like terms and following the rules of arithmetic. Like terms are terms with the same variables raised to the same powers.
To add or subtract polynomial expressions, start by identifying like terms. Next, combine the coefficients of these like terms by either adding or subtracting them. Lastly, write the resulting terms together, rearranging the terms if necessary.
Let’s consider an example:
Example:
Add the polynomial expressions 3x^2 + 2x + 5 and 2x^2 – 4x + 2.
To solve this problem, we first identify the like terms. In this case, the like terms are the terms with the same powers of x.
- The like terms with x^2 are 3x^2 and 2x^2.
- The like terms with x are 2x and -4x.
- The constant terms are 5 and 2.
- The coefficient of x^2 is 3 + 2 = 5.
- The coefficient of x is 2 – 4 = -2.
- The constant term is 5 + 2 = 7.
We can now add the coefficients of the like terms:
Combining these results, the sum of the polynomial expressions 3x^2 + 2x + 5 and 2x^2 – 4x + 2 is 5x^2 – 2x + 7.
In summary, when adding or subtracting polynomial expressions, it is important to identify like terms and combine their coefficients. Following these steps will allow you to simplify polynomial expressions and work with them effectively.
Multiplication and Division of Polynomial Expressions |
|
In algebra, polynomial expressions are mathematical expressions that consist of variables and constants combined using addition, subtraction, multiplication, and exponentiation. Multiplication and division of polynomial expressions are fundamental operations in algebraic calculations and are essential for solving equations and simplifying expressions. When multiplying polynomial expressions, we apply the distributive property to combine the terms. We multiply each term of one polynomial expression by each term of the other expression and then simplify the resulting expression by combining like terms. For example, when multiplying (2x + 3) by (x – 4), we multiply each term of the first polynomial by each term of the second polynomial to get 2x^2 – 5x – 12. This process is known as multiplying polynomials. Similarly, when dividing polynomial expressions, we can use long division or synthetic division to determine the quotient and remainder. Long division involves dividing each term of the polynomial by the divisor and subtracting the resulting product from the dividend, while synthetic division is a quicker method that uses the coefficients of the polynomial. The quotient of the division represents the result of dividing the polynomial expressions, while the remainder represents the leftover terms. Understanding the multiplication and division of polynomial expressions is crucial for various applications in mathematics, science, engineering, and other fields. It allows us to manipulate and simplify complex equations, solve problems, and analyze relationships between variables. Mastery of these operations is essential for success in algebra and beyond. |