In mathematics, quadratic functions are some of the most fundamental and influential types of functions. They are characterized by their ability to model parabolic shapes and represent a wide variety of real-world phenomena. Understanding the key characteristics of quadratic functions is essential for solving problems and making accurate predictions.
One of the key characteristics of quadratic functions is their vertex. The vertex is the point on the graph where the function reaches its maximum or minimum value, depending on whether the parabola opens upward or downward. It is represented as (h, k), where h is the x-coordinate and k is the y-coordinate. The vertex is a crucial point for analyzing the behavior of the function and determining its key features.
Another important characteristic of quadratic functions is the axis of symmetry. The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves. It is represented by the equation x = h, where h is the x-coordinate of the vertex. The axis of symmetry provides valuable information about the symmetry and the range of the function.
Lastly, the key characteristic of quadratic functions is their concavity. A quadratic function can have one of two possible concavities: upward or downward. The concavity determines whether the function opens upward or downward and is identified by the leading coefficient of the quadratic equation. If the leading coefficient is positive, the parabola opens upward, while a negative leading coefficient indicates a parabola that opens downward.
Characteristics of Quadratic Functions Answer Key
A quadratic function is a polynomial function of degree 2, meaning it has terms with exponents up to 2. Quadratic functions can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. Understanding the characteristics of quadratic functions is essential in graphing, solving equations, and analyzing real-world problems. This answer key provides an explanation of two key characteristics of quadratic functions.
1. Vertex
The vertex is a crucial characteristic of a quadratic function. It represents the point at which the function reaches its maximum or minimum value. In the standard form of a quadratic function, f(x) = ax^2 + bx + c, the x-coordinate of the vertex can be found using the formula x = -b/2a. Substituting this value back into the equation, the corresponding y-coordinate can be found. The vertex can also be determined by completing the square or by using graphing calculators.
2. Axis of Symmetry
The axis of symmetry is a vertical line that passes through the vertex of a quadratic function. It divides the parabolic graph into two symmetrical halves. The equation for the axis of symmetry is x = -b/2a, which is the same as the x-coordinate of the vertex. This line is a line of symmetry, meaning that if you fold the graph along this line, the two halves will coincide. The axis of symmetry can also be determined by graphing calculators or by analyzing the equation.
Understanding the vertex and axis of symmetry of quadratic functions allows for easier graphing and analysis of their behavior. These characteristics provide valuable information about the direction of the parabola, the vertex point, and the symmetry of the graph. They are essential tools for solving problems involving quadratic functions in real-life applications.
Definition of a Quadratic Function
A quadratic function is a type of mathematical function that can be expressed using an equation of the form:
f(x) = ax^2 + bx + c
Where a, b, and c are constants and x is the independent variable.
This equation represents a curve called a parabola, which is a U-shaped curve that opens either upwards or downwards. The coefficient a determines the direction of the opening: if a > 0, the parabola opens upwards, and if a < 0, the parabola opens downwards.
The constants a, b, and c in the quadratic equation have specific meanings. The coefficient a determines the steepness of the parabola, with larger values of a resulting in a steeper curve. The coefficient b affects the horizontal position of the vertex of the parabola, while the constant c is the y-coordinate of the vertex.
Quadratic functions have several important characteristics. The vertex of the parabola represents the minimum or maximum point of the function, depending on whether it opens upwards or downwards. The x-coordinate of the vertex can be found using the formula: x = -b / (2a). The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetric halves.
Quadratic functions also have x-intercepts, which are the values of x where the function crosses the x-axis. These can be found by solving the quadratic equation ax^2 + bx + c = 0. The y-intercept is the value of y when x = 0, and it can be found by evaluating f(0). By examining the equation and these characteristics, the overall shape and behavior of the quadratic function can be determined.
Graphical Representation of Quadratic Functions
Quadratic functions are mathematical functions that can be represented graphically using a parabola. A parabola is a U-shaped curve with a vertex. The vertex of the parabola represents the minimum or maximum point of the quadratic function. The direction of the parabola, its concavity, is determined by the coefficient of the quadratic term. If the coefficient is positive, the parabola opens upwards, and if the coefficient is negative, the parabola opens downwards.
One characteristic of a quadratic function is its axis of symmetry, which is a vertical line that passes through the vertex of the parabola. The equation of the axis of symmetry can be found by using the formula x = -b/2a, where a and b are the coefficients of the quadratic function. The axis of symmetry divides the parabola into two symmetrical halves.
Another characteristic of a quadratic function is the roots or zeros of the function. These are the values of x where the parabola intersects the x-axis. The roots can be found by solving the quadratic equation ax^2 + bx + c = 0. The number of roots and their nature (real or complex) depends on the discriminant of the quadratic equation, which is b^2 – 4ac.
By analyzing the graph of a quadratic function, we can determine its vertex, axis of symmetry, roots, and the direction in which it opens. This graphical representation helps us understand the behavior of the function and make predictions about its values for different inputs. It also allows us to solve real-life problems that can be modeled using quadratic functions, such as finding the maximum or minimum values of a certain quantity.
Key Features of Quadratic Functions
A quadratic function is a polynomial function of degree two, typically in the form of f(x) = ax^2 + bx + c. Quadratic functions have several key features that help us understand their behavior and analyze their properties.
Vertex
The vertex is a key feature of a quadratic function and represents the highest or lowest point on the graph. The x-coordinate of the vertex can be found using the formula x = -b/2a. The y-coordinate of the vertex can be found by substituting the x-coordinate into the function. The vertex can indicate the minimum or maximum value of the function.
Axis of Symmetry

The axis of symmetry is a vertical line that passes through the vertex and divides the graph of the quadratic function into two equal halves. The equation of the axis of symmetry can be found using the formula x = -b/2a. The axis of symmetry can help us find the x-values where the function is symmetric.
Intercepts
The x-intercepts, also known as zeroes or roots, are the x-values at which the graph of the quadratic function intersects the x-axis. These can be found by solving the quadratic equation f(x) = 0. The y-intercept is the point where the graph of the function intersects the y-axis. It can be found by substituting x = 0 into the function.
Concavity
The concavity of a quadratic function refers to the direction in which the graph opens. A quadratic function can open upwards, forming a U-shape, or downwards, forming an inverted U-shape. The concavity is determined by the sign of the coefficient a in the quadratic equation. If a is positive, the graph opens upwards, and if a is negative, the graph opens downwards.
Increasing and Decreasing Intervals

A quadratic function can have intervals where it is increasing or decreasing. An increasing interval is where the function values are getting larger as x increases, and a decreasing interval is where the function values are getting smaller as x increases. These intervals can be determined by the sign of the coefficient a and by analyzing the vertex of the quadratic function.
- If a > 0, the function is increasing to the left and right of the vertex.
- If a < 0, the function is decreasing to the left and right of the vertex.
Understanding these key features of quadratic functions allows us to analyze and interpret their graphs, solve real-world problems, and make predictions about their behavior. These features provide valuable insights into the characteristics and properties of quadratic functions.
Vertex Form of a Quadratic Function
The vertex form provides a more convenient way to analyze the characteristics of a quadratic function, as it directly gives the vertex of the parabola. The value of a determines whether the parabola opens upwards (if a > 0) or downwards (if a < 0), while the values of h and k determine the position of the vertex. If a > 0, the vertex is the lowest point on the graph, and if a < 0, the vertex is the highest point on the graph.
By analyzing the vertex form, we can easily determine several characteristics of the quadratic function. For example, the vertex form allows us to identify the vertex, the direction the parabola opens, and the axis of symmetry. It also helps in finding the maximum or minimum value of the function, as the vertex represents the maximum or minimum point of the parabola.
In conclusion, the vertex form of a quadratic function is a powerful tool that simplifies the analysis of the function by providing the coordinates of the vertex. It allows us to easily determine important characteristics of the function, such as the direction the parabola opens, the axis of symmetry, and the maximum or minimum value. By understanding the vertex form, we can gain valuable insights into the behavior of quadratic functions.
Factored Form of a Quadratic Function
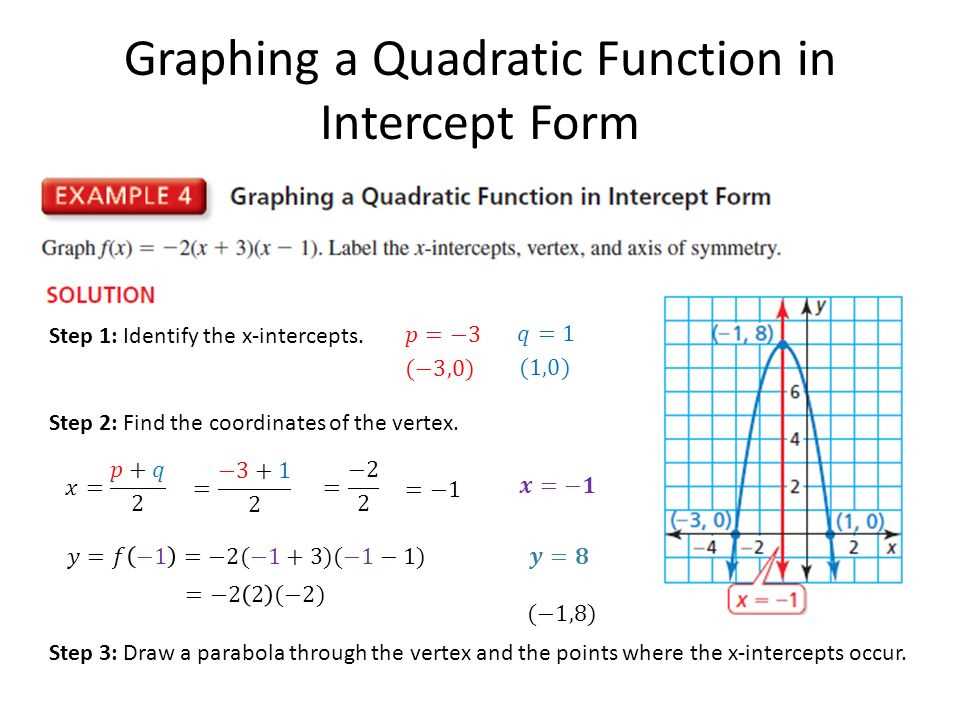
The factored form of a quadratic function is a way to express the function in terms of its roots or zeros. It is also known as the factored form or the zero product property form. In this form, the quadratic function is written as a product of its linear factors. For a quadratic function in factored form, the x-intercepts or zeros of the function can be easily identified from the expression.
To understand the factored form of a quadratic function, let’s consider an example:
Suppose we have a quadratic function f(x) = (x – 2)(x + 3). In this function, the linear factors are (x – 2) and (x + 3). The factored form tells us that the quadratic function has zeros at x = 2 and x = -3. This means that the graph of the function will intersect the x-axis at x = 2 and x = -3. These points are also known as the x-intercepts or zeros of the function.
The factored form of a quadratic function provides valuable information about the graph of the function. It allows for easy identification of the x-intercepts or zeros, which are important points on the graph. Additionally, the factored form helps in solving quadratic equations and finding the solutions to the equation. By setting the function equal to zero and factoring, we can find the values of x that make the function equal to zero.
In summary, the factored form of a quadratic function is a useful representation that expresses the function in terms of its linear factors. It allows for easy identification of the x-intercepts or zeros of the function and helps in solving quadratic equations.
Finding the Axis of Symmetry
The axis of symmetry is an important characteristic of a quadratic function. It is a vertical line that divides the graph of a quadratic function into two symmetrical halves. Finding the axis of symmetry is crucial for understanding the behavior and properties of the function.
To find the axis of symmetry, we can use the formula x = -b/2a, where a, b, and c are the coefficients of the quadratic function in the general form ax^2 + bx + c. The axis of symmetry is the x-coordinate of the vertex of the parabola represented by the quadratic function.
For example, let’s consider the quadratic function f(x) = 2x^2 + 4x – 1. By using the formula x = -b/2a, we can calculate the x-coordinate of the axis of symmetry. In this case, a = 2 and b = 4. Plugging these values into the formula, we get x = -4/(2*2) = -4/4 = -1. Therefore, the axis of symmetry for this quadratic function is x = -1.
The axis of symmetry has several important properties. Firstly, any point on the parabola that lies on the axis of symmetry has the same y-coordinate. Secondly, the axis of symmetry is equidistant from the two x-intercepts of the parabola, which are the points where the parabola intersects the x-axis. Lastly, the axis of symmetry is a vertical line that divides the parabola into two symmetrical halves.
Understanding and finding the axis of symmetry is essential for graphing quadratic functions, determining important points on the graph, and analyzing the behavior of the function. It provides valuable information about the symmetry and shape of the parabola represented by the quadratic function.
Finding the Vertex of a Quadratic Function
A quadratic function is a type of polynomial function with a degree of 2. It can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants.
The vertex of a quadratic function is the point where the function reaches its minimum or maximum value. It is also the point where the graph of the function intersects the axis of symmetry. The axis of symmetry is a vertical line that passes through the vertex and divides the parabola into two symmetrical halves.
To find the vertex of a quadratic function, you can use different methods, such as completing the square or using the vertex formula. One common method is to use the vertex formula x = -b/2a. This formula gives the x-coordinate of the vertex. Once you have the x-coordinate, you can substitute it back into the quadratic function to find the y-coordinate.
For example, let’s consider the quadratic function f(x) = 2x^2 + 4x – 3. By using the vertex formula x = -b/2a, we can calculate the x-coordinate of the vertex. In this case, a = 2 and b = 4, so x = -4/(2*2) = -1. Once we have the x-coordinate, we can substitute it back into the function to find the y-coordinate. Plugging in x = -1, we get f(-1) = 2(-1)^2 + 4(-1) – 3 = -1. Therefore, the vertex of the quadratic function is (-1, -1).
Understanding how to find the vertex of a quadratic function is crucial for various applications, such as optimizing a process, solving real-life problems, or analyzing data. The vertex provides valuable information about the behavior and characteristics of the quadratic function.