Proportional relationships play a crucial role in various mathematical and real-life scenarios. Understanding and comparing these relationships is essential to make informed decisions and solve problems accurately. In this article, we will explore the answer key for comparing proportional relationships, providing you with the necessary tools to analyze and interpret the relationship between two sets of data.
When comparing two proportional relationships, it is important to look at their slopes or rates of change. The slope represents the rate at which one variable changes in relation to the other. By calculating the slopes of both relationships, you can determine which one is steeper or shows a higher rate of change.
In addition to comparing slopes, it is crucial to consider the y-intercept of the relationships. The y-intercept represents the starting point of the relationship, where the value of the dependent variable is zero. Examining the y-intercepts can help identify any shifts or variations in the proportional relationship.
Furthermore, analyzing the answers and comparing proportional relationships involves looking at their graphs or tables. Graphically representing the relationships can provide a visual representation of how the variables are related. By comparing these graphs or tables, you can easily identify any patterns or differences between the relationships and gain a deeper understanding of their characteristics.
In conclusion, comparing proportional relationships requires considering various factors, such as slopes, y-intercepts, and graphical representations. By utilizing the answer key and applying these techniques, you can effectively analyze and interpret the relationship between two sets of data, enabling you to make informed decisions and solve problems accurately.
Understanding Proportional Relationships
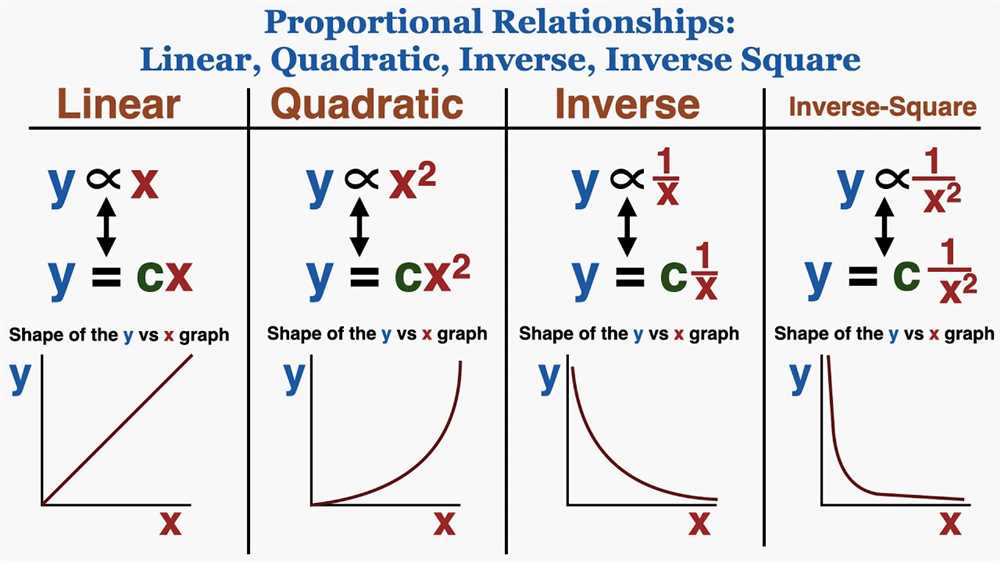
A proportional relationship is a special type of relationship between two quantities in which the ratio of one quantity to the other remains constant. This means that as one quantity increases, the other quantity also increases in a consistent manner. Conversely, as one quantity decreases, the other quantity decreases in the same proportion.
One way to understand proportional relationships is through the concept of unit rate. A unit rate is the rate at which one quantity changes in relation to one unit change in another quantity. For example, if a car travels 60 miles in 2 hours, the unit rate would be 30 miles per hour. This means that for every 1 hour, the car travels 30 miles.
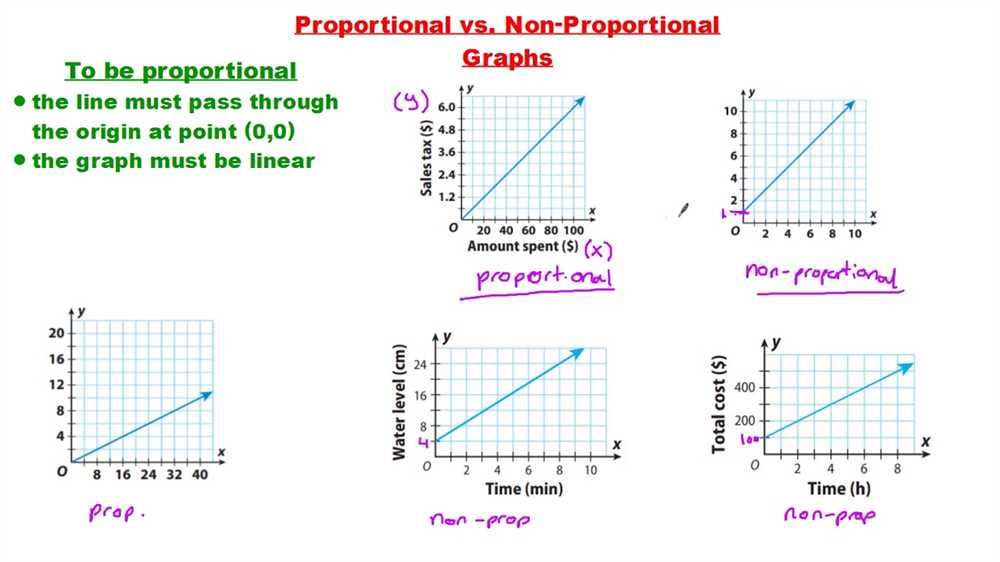
Proportional relationships can be represented graphically, algebraically, or through tables. Graphically, a proportional relationship will appear as a straight line passing through the origin (0, 0). Algebraically, a proportional relationship can be represented by an equation of the form y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality. In a table, a proportional relationship will have constant ratios between the values of the two quantities.
Understanding proportional relationships is important in various real-world situations. For example, in business, knowing the proportional relationship between cost and quantity can help in determining the most cost-effective production levels. In science, understanding proportional relationships is crucial in analyzing and interpreting experimental data. Additionally, in everyday life, recognizing and utilizing proportional relationships can aid in making informed decisions and solving problems efficiently.
What are proportional relationships?
A proportional relationship is a mathematical concept that describes the relationship between two variables in which the ratio of their values remains constant. In other words, as one variable increases or decreases, the other variable changes at a consistent rate. This relationship can be represented by a straight line on a graph.
In a proportional relationship, the constant ratio between the two variables is called the “constant of proportionality.” This constant represents how much one variable changes for every unit change in the other variable. It can be found by dividing the value of one variable by the corresponding value of the other variable.
For example, if the price of apples is directly proportional to the weight of apples, and the constant of proportionality is $2 per pound, then for every additional pound of apples you buy, the price will increase by $2. This means that if you buy 3 pounds of apples, the total price will be $6 more than if you bought 1 pound.
Proportional relationships are often represented using a ratio table or a graph. In a ratio table, the values of the two variables are listed side by side, and the ratio of their values remains constant. On a graph, the points representing the values of the two variables will lie on a straight line that passes through the origin (0,0).
Understanding proportional relationships is important in various fields, such as economics, physics, and statistics. It allows us to analyze how two variables are related and predict how changes in one variable will affect the other. Proportional relationships provide a foundational concept in mathematics and are essential for solving many real-world problems.
How to identify proportional relationships?
In mathematics, proportional relationships exist when two quantities are related in such a way that one is a constant multiple of the other. This means that as one quantity increases or decreases, the other quantity changes proportionally by the same factor. To identify proportional relationships, one can use several methods.
Method 1: Calculate the ratio
One way to determine if a relationship is proportional is by calculating the ratio between the values of the two quantities. If the ratio remains the same for all the data points, then the relationship is proportional. For example, if the ratio of the values of quantity A to quantity B is always 2:1, then the relationship between A and B is proportional.
Method 2: Graph the data
Another way to identify proportional relationships is by graphing the data points on a coordinate plane. If the points lie on a straight line that passes through the origin (0,0), then the relationship is proportional. This indicates that the change in one quantity depends linearly on the change in the other quantity.
Method 3: Use the constant of proportionality
In some cases, the relationship between two quantities can be expressed by a specific equation. This equation includes a constant of proportionality, which is the value by which one quantity is multiplied to obtain the other quantity. If the constant of proportionality remains the same for all data points, then the relationship is proportional.
By applying these methods, one can easily identify and recognize proportional relationships in mathematical problems or real-life situations. Understanding proportional relationships is essential for various applications, such as scaling, ratio analysis, and solving proportion word problems in everyday life and advanced mathematics.
Comparing Proportional Relationships
Understanding Proportions
Proportional relationships play a crucial role in various mathematical concepts. When we say two quantities are directly proportional, it means that as one quantity increases, the other quantity also increases at a constant rate. In other words, there is a consistent ratio between these two quantities. Understanding proportions is important because they help us solve real-world problems involving rates, scaling, and comparisons.
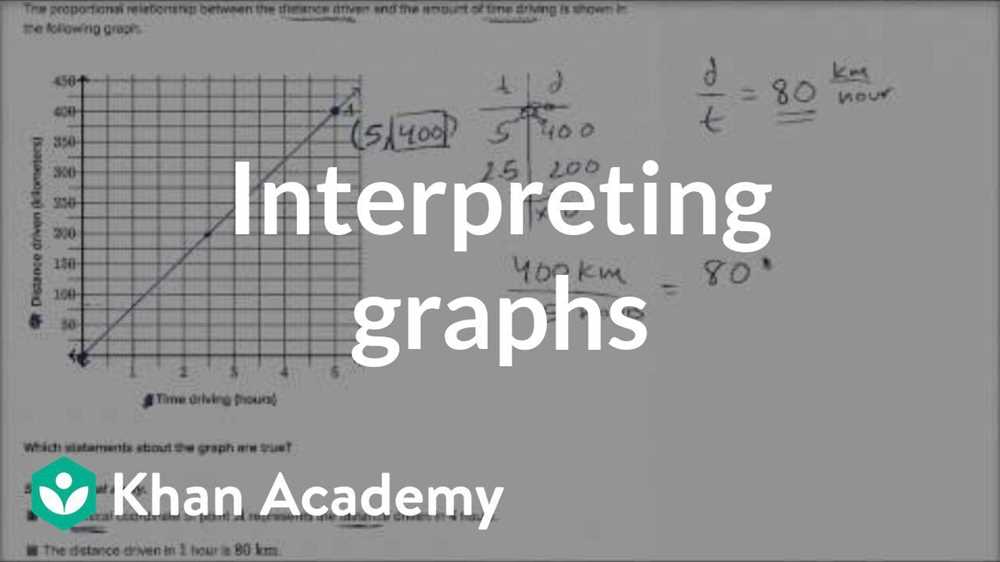
One way to compare proportional relationships is by examining their graphs. Graphs can provide a visual representation of how the quantities change in relation to each other. By analyzing the slopes of the graphs, we can determine whether the two relationships have the same rate of change or if one is steeper than the other. This helps us understand which relationship is more proportional and makes it easier to make comparisons.
Comparing Ratios
Another way to compare proportional relationships is by comparing their ratios. Ratios help us understand the relationship between two quantities and can be expressed in various forms, such as fractions, decimals, or percentages. By comparing the ratios, we can determine which relationship has a larger or smaller proportion. For example, if one ratio is 3:4 and another is 2:5, we can see that the second relationship has a larger proportion.
- Key Point: Comparing proportional relationships involves analyzing their graphs and ratios to determine which relationship is more proportional or has a larger proportion.
Being able to compare proportional relationships is crucial in analyzing data, making predictions, and understanding patterns. It allows us to identify trends and make informed decisions in various fields, including economics, science, and everyday life. Therefore, developing a strong understanding of proportional relationships and their comparisons is essential for mathematical proficiency.
Why is it important to compare proportional relationships?
Comparing proportional relationships is an important skill in mathematics that allows us to understand and analyze different scenarios involving quantities and their relationships. By comparing proportional relationships, we can make informed decisions, predict outcomes, and identify patterns and trends.
One reason why it is important to compare proportional relationships is for problem solving. Proportional relationships often arise in real-world situations, such as sales data, rates, or ratios, and being able to compare these relationships helps us solve problems more effectively. For example, if we are analyzing sales data for different products, comparing their proportional relationships can help us determine which product is selling the most and identify any patterns or trends in the data.
Another reason why comparing proportional relationships is important is for making predictions. When we compare the relationships between different variables, we can use that information to predict future outcomes. For example, if we are studying the relationship between time and distance, comparing different proportional relationships can help us predict how far an object will travel in a given amount of time.
Furthermore, comparing proportional relationships helps us identify patterns and trends. By analyzing different proportional relationships, we can look for similarities or differences in how quantities change together. This can lead to valuable insights and allow us to make better decisions based on the observed patterns and trends. For example, by comparing the proportional relationships of temperature and ice cream sales, we may discover that there is a positive correlation between the two, suggesting that hotter temperatures lead to higher ice cream sales.
In conclusion, comparing proportional relationships is important because it enhances our problem-solving abilities, allows us to make predictions, and helps us identify patterns and trends. It is a fundamental skill in mathematics and provides us with valuable insights in understanding and analyzing the world around us.
Methods for comparing proportional relationships
When comparing proportional relationships, there are several methods that can be used to determine their similarities and differences. These methods allow us to analyze the relationships between variables and make comparisons based on their proportions.
1. Graphical representation: One method for comparing proportional relationships is by graphing the data points on a coordinate plane. This visual representation allows us to see the patterns and trends in the data and identify any similarities or differences between the relationships.
2. Calculation of slopes: Another method involves calculating the slopes of the proportional relationships. The slope represents the rate of change between the variables, and comparing the slopes allows us to determine if the relationships are similar or different. If the slopes are equal, the relationships are proportional; if they are not equal, then they are not proportional.
3. Proportional reasoning: Proportional reasoning involves analyzing the ratios between the variables in the relationships. By comparing the ratios, we can determine if they are proportional or not. For example, if the ratios between the variables are equal for both relationships, then they are proportional. If the ratios are not equal, then they are not proportional.
4. Table comparison: Another method involves creating tables to compare the values of the variables in the relationships. By comparing the values in the tables, we can determine if they follow a consistent pattern, indicating a proportional relationship. If the values do not follow a consistent pattern, then the relationships are not proportional.
By using these methods, we can effectively compare proportional relationships and make accurate conclusions about their similarities and differences. These techniques help us analyze data and make informed decisions based on the patterns and trends in the relationships.
Answer Key for Proportional Relationship Comparison
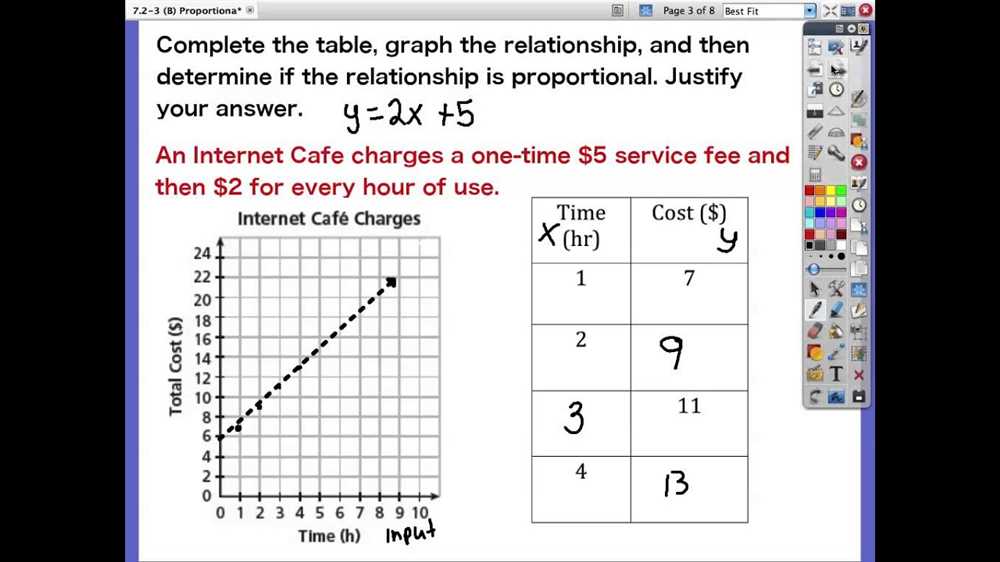
When comparing proportional relationships, it is important to analyze both the constant of proportionality and the initial value. These two components provide key information about how the relationships are related and can help determine which relationship is stronger or more significant.
The constant of proportionality, often represented by the letter “k,” is a numerical value that relates the two variables in a proportional relationship. It indicates the rate at which the dependent variable changes as the independent variable changes. Higher values of the constant of proportionality indicate a stronger relationship, as the values of the dependent variable increase at a faster rate.
For example, if we compare two proportional relationships with equal initial values but different constants of proportionality, we can determine which relationship is stronger. Let’s consider the relationships y = 2x and y = 5x. Both relationships have an initial value of 0, but the second relationship has a larger constant of proportionality. This means that for every increase of 1 in the independent variable, the dependent variable increases by 5 units, compared to only 2 units in the first relationship. Therefore, the second relationship is stronger, as the values of the dependent variable increase at a faster rate.
In addition to the constant of proportionality, the initial value of a proportional relationship also plays a crucial role in determining the strength of the relationship. The initial value represents the starting point of the relationship, where both variables have a value of 0. Comparing the initial values of two proportional relationships can help identify which relationship has a higher starting point.
For instance, let’s compare the relationships y = 2x and y = 2x + 5. Both relationships have the same constant of proportionality, but the second relationship has an initial value of 5. This means that when the independent variable is 0, the dependent variable already has a value of 5, compared to 0 in the first relationship. Therefore, the second relationship has a higher starting point and can be considered stronger in terms of its initial value.
In conclusion, when comparing proportional relationships, analyzing the constant of proportionality and the initial value is essential. These two components provide valuable insights into the strength and significance of the relationships and can help determine which relationship is stronger or more impactful.