If you enjoy solving puzzles and have a passion for geometry, the 2 6 Puzzle Time is the perfect challenge for you. This puzzle combines your knowledge of geometric shapes and concepts with problem-solving skills to arrive at the correct answers.
The 2 6 Puzzle Time consists of various geometry-based questions that require you to analyze and apply your understanding of different geometric properties. These questions can range from identifying angles and shapes, to calculating areas and perimeters. By solving these puzzles, you can enhance your spatial reasoning and logical thinking abilities.
Answering the 2 6 Puzzle Time questions provides you with an opportunity to engage your brain and explore the intricacies of geometry in a fun and interactive way. As you progress through the puzzles, you’ll not only strengthen your knowledge of geometric principles, but also develop problem-solving strategies that can be applied in various real-life scenarios.
So, if you’re ready to put your geometry skills to the test and enjoy the thrill of solving puzzles, dive into the world of 2 6 Puzzle Time and see how far you can go!
Puzzle Time Answers Geometry
Geometry is a branch of mathematics that focuses on the properties, measurement, and relationship of points, lines, angles, and surfaces. It is widely used in various fields, including engineering, architecture, and art. Understanding geometry concepts and solving geometry problems can be challenging, but puzzle time answers provide a fun and engaging way to practice and reinforce geometric knowledge.
Puzzle time answers in geometry often involve solving puzzles or riddles that require geometric reasoning and problem-solving skills. These puzzles can be in the form of diagrams, word problems, or visual patterns. They may involve finding missing angles in shapes, determining the area or perimeter of polygons, or solving geometric equations.
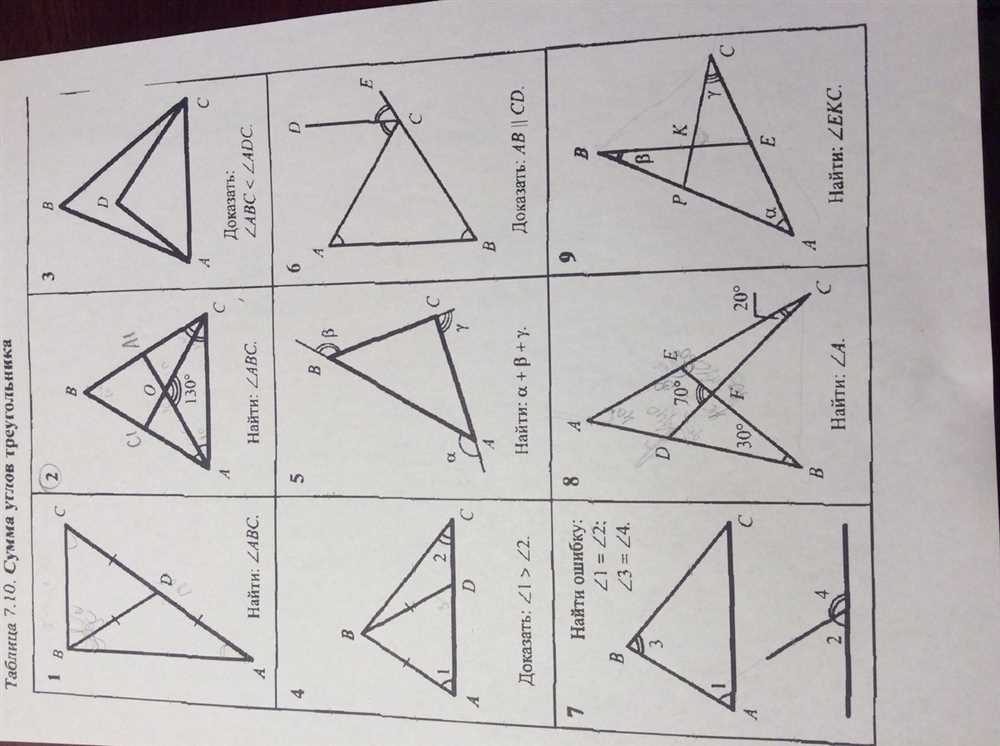
One example of a puzzle time answer in geometry is finding the missing angle measures in a triangle. Given the measures of two angles in a triangle, students can use the fact that the sum of all angles in a triangle is 180 degrees to find the missing angle. This puzzle time answer helps students practice their understanding of angle properties and relationships.
Another example of a puzzle time answer in geometry is determining the area of a complex shape. Students may be given a shape composed of multiple polygons and asked to find the total area. They can do this by breaking down the shape into smaller, simpler polygons, finding their individual areas, and then summing them up. This puzzle time answer allows students to apply their knowledge of area formulas and decomposition strategies.
Overall, puzzle time answers in geometry provide an interactive and engaging way for students to practice and apply their geometric skills. By solving puzzles and challenges, students can develop a deeper understanding of geometric concepts and improve their problem-solving abilities in the context of geometry.
Understanding the 26 Puzzle
The 26 Puzzle is a geometric puzzle that challenges players to arrange 12 pieces in a 3×3 square, leaving one empty space. The objective is to move the pieces around the board using sliding motions, with the goal of arranging them in a specific pattern. This puzzle requires strategic thinking and spatial reasoning skills to solve.
To solve the 26 Puzzle, players must carefully plan their moves and visualize the end result. Each piece can only slide into the empty space, so it is crucial to create a pathway for the pieces to move around the board. This requires analyzing the current arrangement of the pieces and identifying the best sequence of moves to reach the desired pattern.
The geometry of the puzzle comes into play when determining the possible movements of each piece. The pieces can only slide horizontally or vertically, which limits their range of motion. This constraint adds an extra layer of complexity to the puzzle, as players must consider the positioning of the pieces in relation to the empty space in order to make successful moves.
One strategy for solving the 26 Puzzle is to start by moving the pieces around the board to create a pattern that resembles the desired final arrangement. From there, players can work towards achieving the specific pattern by making calculated moves. This approach requires patience and careful observation, as players must constantly assess the impact of each move on the overall arrangement.
In conclusion, the 26 Puzzle is a challenging geometric puzzle that tests players’ spatial reasoning skills. By carefully planning their moves and considering the geometry of the puzzle, players can work towards solving it and achieving the desired pattern. With practice and persistence, anyone can become proficient at solving the 26 Puzzle.
The Significance of Geometry in the 26 Puzzle
In the 26 Puzzle, geometry plays a crucial role in finding the correct solution. The puzzle consists of a grid with 26 letters arranged in a specific order. The objective is to find a path that connects all the letters in alphabetical order by moving horizontally, vertically, or diagonally. With the help of geometry, one can analyze the grid’s structure and identify possible paths to complete the puzzle.
Geometry provides the necessary tools to understand the spatial relationships within the grid. By examining the angles and distances between adjacent letters, one can determine the most efficient path to navigate through the puzzle. Additionally, geometric concepts such as symmetry and congruence can be applied to identify patterns or mirror images that might exist within the grid, leading to potential solutions.
Angles: Understanding the angles formed by the grid’s lines is essential in determining the direction of the path. By recognizing acute, obtuse, or right angles, one can decide whether to navigate diagonally or stick to horizontal and vertical movements. The ability to estimate angles also helps in assessing the feasibility of certain paths and avoiding dead ends.
Distances: Geometry enables the measurement of distances between letters, allowing for an accurate estimation of the length of potential paths. By calculating distances, one can determine the shortest or longest routes to connect the letters in alphabetical order. This knowledge helps in making informed decisions and optimizing the solving process.
Symmetry and Congruence: Analyzing the grid for symmetrical patterns or congruent shapes can lead to shortcuts or alternative routes to complete the puzzle. Identifying symmetrical pairs or groups of letters allows for the recognition of possible mirror image paths, reducing the complexity of the problem. Recognizing congruent shapes can help in visualizing certain paths and eliminating incorrect options.
In conclusion, geometry plays a significant role in solving the 26 Puzzle effectively. It provides the necessary tools to analyze the spatial relationships, estimate distances, navigate angles, and identify patterns within the grid. By leveraging these geometric concepts, one can approach the puzzle strategically and find the correct path to connect all the letters in alphabetical order.
Key Concepts and Formulas in Geometry
In geometry, there are several key concepts and formulas that are essential to understanding and solving problems. These concepts and formulas are used to calculate distances, angles, areas, and volumes, and are fundamental to solving geometric problems.
1. Pythagorean Theorem: The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It can be represented as a^2 + b^2 = c^2, where a and b are the lengths of the two shorter sides and c is the length of the hypotenuse.
2. Area Formulas: In geometry, there are different formulas to calculate the area of different shapes. For example, for a rectangle, the area is calculated by multiplying the length and width: A = l × w. Similarly, the area of a triangle can be calculated using the formula A = 1/2 × b × h, where b is the base of the triangle and h is the height.
3. Angle Relationships: Understanding angle relationships is important in geometry. Some key concepts include complementary angles (two angles whose sum is 90 degrees), supplementary angles (two angles whose sum is 180 degrees), and vertical angles (opposite angles formed by the intersection of two lines).
4. Theorems: Theorems are important in geometry as they provide rules that can be used to prove various properties and relationships. Some notable theorems include the Pythagorean theorem, which we discussed earlier, and the Angle Bisector theorem, which states that an angle bisector divides the opposite side of a triangle into segments that are proportional to the lengths of the other two sides.
5. Volume Formulas: Volume formulas are used to calculate the amount of space occupied by a three-dimensional shape. For example, the volume of a rectangular prism can be calculated by multiplying the length, width, and height: V = l × w × h. Similarly, the volume of a sphere can be calculated using the formula V = 4/3 × π × r^3, where r is the radius of the sphere.
- Overall, understanding key concepts and formulas in geometry is crucial for solving geometric problems.
- It is important to remember and apply the Pythagorean theorem to solve problems involving right-angled triangles.
- Being familiar with area formulas for different shapes helps in calculating the area accurately.
- Understanding angle relationships and theorems can aid in proving various properties and solving geometry problems.
- Volume formulas are used to find the amount of space occupied by three-dimensional shapes.
Solving the 26 Puzzle Using Geometry
The 26 puzzle is a fascinating mathematical challenge that requires solving a series of geometric equations. This puzzle involves arranging the numbers 2 through 6 in a grid, such that each row and column adds up to 26. To solve this puzzle, a deep understanding of geometry is essential.
Geometry plays a crucial role in solving the 26 puzzle because it helps determine the relationship between the numbers and their positions in the grid. One key geometric concept that comes into play is symmetry. By utilizing the symmetry properties of the grid, it becomes possible to find the correct arrangement for the numbers.
Another important geometrical concept used in solving the 26 puzzle is the concept of diagonals. By analyzing the diagonals of the grid, one can identify potential values for the missing numbers and narrow down the possible arrangements accordingly.
To solve the 26 puzzle, one must also be familiar with geometric transformations such as rotations and reflections. By applying these transformations to the initial arrangement of the numbers, different possibilities can be explored and evaluated to find the correct solution.
In conclusion, solving the 26 puzzle requires a strong grasp of geometry and its various concepts. By understanding the symmetries, diagonals, and transformations within the grid, one can navigate through the problem and find the correct arrangement of numbers that satisfies the given condition.
Step-by-Step Guide to Finding the Answers

When it comes to solving the 2 6 puzzle time geometry questions, it is important to follow a step-by-step approach in order to find the correct answers. These puzzles often require a combination of logic, geometry knowledge, and a systematic way of thinking. By following the steps outlined below, you can improve your chances of finding the right solutions.
Step 1: Read the Question Carefully
Before attempting to solve the puzzle, make sure to read the question carefully and understand what is being asked. Look for any given information, such as measurements or relationships between geometric figures, that can help guide your thought process. Pay close attention to any specific instructions or conditions that are provided.
Step 2: Analyze the Given Information
Next, analyze the given information and try to visualize the geometric figures or shapes involved. Identify any known values, angles, or lengths that are provided and determine how they relate to each other. Draw diagrams if necessary to help visualize the problem.
Step 3: Apply Relevant Geometry Concepts
Once you have a clear understanding of the question and the given information, apply relevant geometry concepts to solve the problem. This may involve using properties of triangles, circles, angles, or other geometric shapes. Use formulas, theorems, and definitions to guide your calculations and reasoning.
Step 4: Work Through the Problem Methodically
As you work through the problem, approach it in a logical and systematic way. Break the problem down into smaller steps or sub-questions if necessary, and solve each part one at a time. Make sure to label your diagrams and equations clearly, and double-check your calculations along the way.
Step 5: Check Your Answer
Finally, once you have found a solution, take the time to double-check your answer. Make sure that your calculations are accurate and that your solution aligns with the given conditions and requirements of the question. If possible, try to verify your answer using a different approach or method.
By following these step-by-step guidelines, you can approach 2 6 puzzle time geometry questions with confidence and improve your problem-solving skills in this area. Remember to practice regularly and seek additional help or resources if needed to enhance your understanding of geometry concepts.
Common Mistakes to Avoid in Geometry Problem Solving
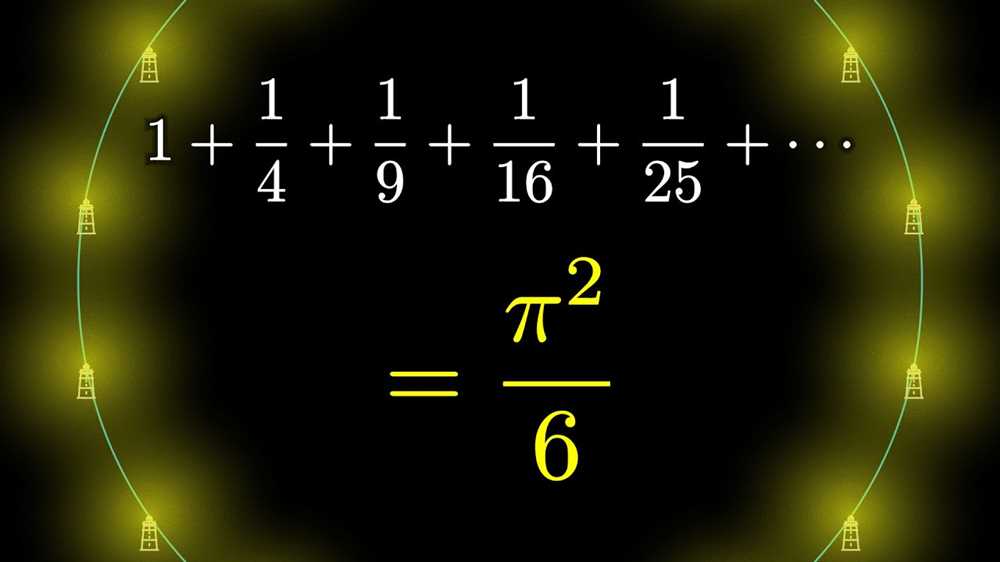
Geometry problem solving can be challenging, but with the right approach and avoiding common mistakes, you can improve your skills and find success in this subject. Here are some common mistakes to avoid when solving geometry problems:
1. Misunderstanding Definitions and Terminology
One of the most common mistakes in geometry problem-solving is misunderstanding or misinterpreting definitions and terminology. It’s essential to have a clear understanding of basic terms like angles, lines, triangles, and polygons. Taking the time to review and familiarize yourself with these definitions can help you avoid confusion and improve your problem-solving skills.
2. Missing Key Information
Another mistake is overlooking or missing key information given in the problem. Geometry problems often provide important details and measurements that are crucial for solving the problem correctly. Carefully read the problem statement and underline or highlight any relevant information. Taking the time to identify and understand the given information can prevent errors and lead to accurate solutions.
3. Incorrect Diagram Representation
A common pitfall in geometry problem solving is creating an inaccurate or incomplete diagram. Geometry relies heavily on visual representation, so it’s crucial to draw an accurate diagram that reflects the given information. Pay attention to measurements, angles, and relationships between geometric elements while creating your diagram. Double-checking your diagram for accuracy can help you correctly apply geometric principles and solve the problem effectively.
4. Not Applying Geometry Concepts Correctly
Geometry problems often require applying various concepts and theorems. One mistake to avoid is not applying these concepts correctly or misusing theorems. It’s important to have a solid foundation of basic geometry principles and understand how to use them in different problem-solving situations. Reviewing and practicing different geometric concepts can improve your ability to apply them correctly and find the correct solution.
5. Lack of Practice
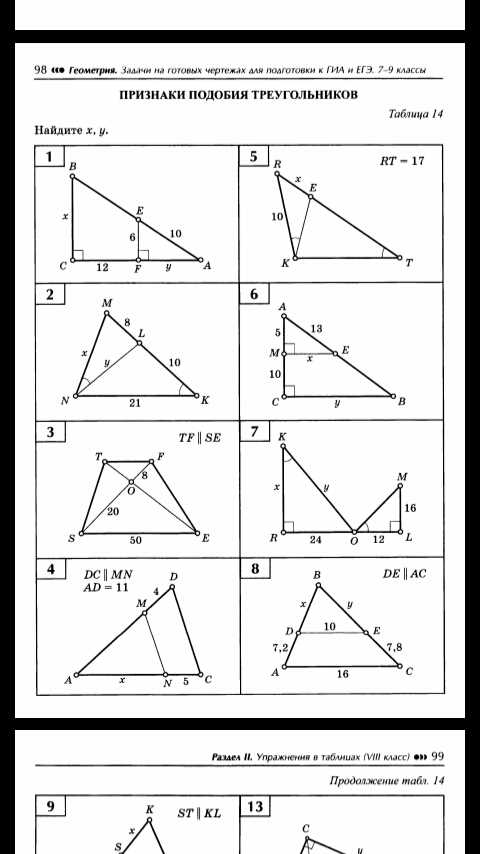
Lastly, a common mistake is not dedicating enough time to practice geometry problems. Geometry requires practice to develop problem-solving skills and improve understanding. Regularly solving geometry problems can help you become familiar with different types of problems, identify patterns, and apply different strategies or approaches. Practice, especially with diverse problem sets, can enhance your problem-solving ability and increase your confidence in tackling geometry problems.
Avoiding these common mistakes in geometry problem solving can help you enhance your skills and improve your success rate in this subject. By understanding definitions, paying attention to key information, creating accurate diagrams, correctly applying geometry concepts, and dedicating time to practice, you can become a more proficient geometry problem solver.