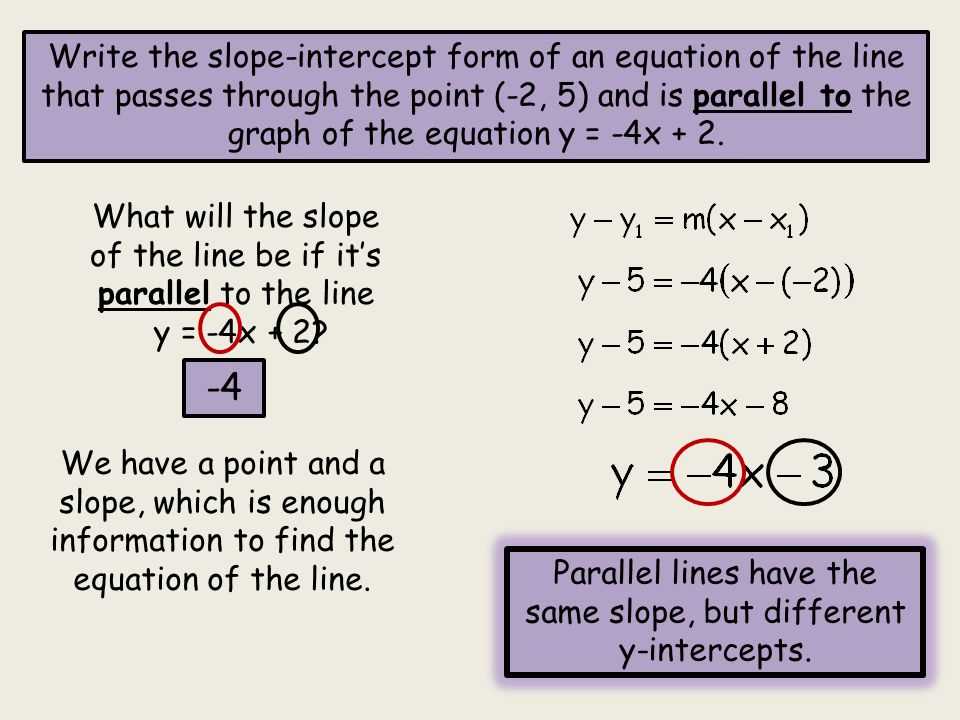
Understanding linear equations and their various forms is essential in mastering the foundations of algebra. One commonly used form is the slope-intercept form, which provides a straightforward way to represent a linear equation. To help you strengthen your skills in this area, this study guide and intervention will provide you with answers to the 3 4 exercises on slope-intercept form.
The slope-intercept form of a linear equation is written as y = mx + b, where m represents the slope of the line and b represents the y-intercept, the point where the line crosses the y-axis. By identifying the values of m and b, you can determine how the line behaves and the relationship between the x and y variables.
In this study guide and intervention, you will find step-by-step solutions for the exercises in the 3 4 section. These exercises involve rewriting equations in slope-intercept form, graphing lines using the slope-intercept form, and solving real-life problems using linear equations. With the provided answers, you will be able to check your work, verify your understanding, and identify any areas that may require further practice.
Mastering slope-intercept form is crucial not only for algebra but also for more advanced mathematics and real-life applications. By completing the exercises and reviewing the answers in this study guide and intervention, you will strengthen your ability to work with linear equations, enhance your problem-solving skills, and build a solid foundation for future mathematical concepts.
Understanding the Concept of Slope
The concept of slope is fundamental in mathematics and plays a crucial role in various fields, including algebra, geometry, physics, and engineering. It represents the measure of how steep or slanted a line is, indicating the rate of change between two points on a graph.
Slope Intercept Form: One of the most common ways to represent a linear equation is in slope-intercept form, which is written as y = mx + b. In this form, m represents the slope of the line, while b represents the y-intercept, which is the point where the line crosses the y-axis. By knowing the values of m and b, we can easily determine the equation of the line and plot it on a graph.
Positive and Negative Slope: The slope can be positive or negative, depending on the direction of the line. A positive slope indicates that the line is rising from left to right, while a negative slope indicates that the line is falling from left to right. The steepness of the slope can be determined by the magnitude of its value.
- Zero Slope: A line with a slope of zero is horizontal and parallel to the x-axis. This means that for every change in x, there is no change in y. The equation of a line with a zero slope is y = b, where b is the y-intercept.
- Undefined Slope: A line with an undefined slope is vertical and parallel to the y-axis. This type of line does not have a numerical value for its slope because division by zero is undefined. The equation of a vertical line is x = a, where a is the x-coordinate of any point on the line.
- Interpreting Slope: The slope not only indicates the steepness of a line but also provides information about the relationship between two variables. For example, in the context of a real-world problem, a positive slope can represent an increase in one quantity as another quantity increases, while a negative slope can represent a decrease in one quantity as another quantity increases.
Applications: The concept of slope is used in various applications, such as calculating velocity in physics, determining the rate of change in economics, analyzing trends in data, designing ramps or inclines, and creating mathematical models to represent real-world phenomena. It is a versatile concept that is essential for understanding and analyzing mathematical relationships.
The Definition of Slope
Slope is a fundamental concept in mathematics that measures how steep a line is. It indicates the rate at which a line rises or falls as it moves along a coordinate plane. In simple terms, slope can be understood as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on a line. It can also be interpreted as the change in the dependent variable divided by the change in the independent variable.
The slope of a line can be positive, negative, zero, or undefined. A positive slope means that as the x-values increase, the y-values also increase. A negative slope means that as the x-values increase, the y-values decrease. A zero slope indicates a horizontal line, where the y-values remain constant regardless of the change in x-values. An undefined slope occurs when the line is vertical, making it impossible to determine a numerical value for the slope.
The slope of a line can be expressed in different forms, one of which is the slope-intercept form. In this form, the slope is represented by the coefficient of the x-term, while the y-intercept (the point where the line crosses the y-axis) is represented by the constant term. The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
Understanding the concept of slope is crucial in various mathematical and real-world applications. It helps in analyzing the relationship between variables, determining the direction and steepness of a line, and solving problems involving rates of change. Whether in algebra, geometry, physics, or economics, slope plays a significant role in describing and predicting patterns, trends, and relationships.
Calculating Slope Using the Slope-Intercept Form
The slope-intercept form of a linear equation is written as y = mx + b, where m represents the slope of the line and b represents the y-intercept.
To calculate the slope of a line using the slope-intercept form, we need to look at the coefficient of x, which is represented by the variable m. The slope of a line is a measure of how steep it is, and it can be positive, negative, or zero.
For example, if we have the equation y = 3x + 2, we can see that the coefficient of x is 3. This means that the slope of the line is 3. This tells us that for every increase of 1 unit in the x-coordinate, the y-coordinate will increase by 3 units.
If the coefficient of x is negative, it means that the line is decreasing as we move from left to right. For example, if we have the equation y = -2x + 4, the slope is -2. This tells us that for every increase of 1 unit in the x-coordinate, the y-coordinate will decrease by 2 units.
Calculating the slope using the slope-intercept form is an essential skill in algebra and can be used to analyze various real-world situations. It allows us to understand how variables are related and make predictions based on the values of these variables.
Recognizing the Intercept in Linear Equations
When working with linear equations in the form of y = mx + b (slope-intercept form), it is important to recognize the meaning of the intercept. The intercept, represented by the variable “b,” is the point where the line intersects the y-axis. It indicates the value of the dependent variable (y) when the independent variable (x) is equal to zero.
By identifying the intercept, we can determine the starting point of the line on the y-axis. This information is helpful in graphing the equation and understanding its properties. The intercept can be positive, negative, or zero, depending on the equation. The sign of the intercept indicates whether the line intersects the y-axis above or below the origin.
To find the intercept, we can set x = 0 and solve the equation for y. This will give us the specific value of y when x is equal to zero. By plugging in different values for x and y, we can then plot points on the graph and connect them to form a straight line.
It is important to note that the intercept is just one piece of information necessary to graph a linear equation. The slope (represented by the variable “m”) is also crucial in determining the steepness of the line. By combining the intercept and slope, we can accurately graph any linear equation in slope-intercept form.
Interpreting the y-Intercept
When working with linear equations in slope-intercept form, the y-intercept is an important concept to consider. The y-intercept is the point where the line intersects the y-axis. It is the value of y when x is equal to 0. In the equation y = mx + b, the value of b represents the y-intercept.
The y-intercept has several implications and can provide valuable information about the equation and the graph of the line. It tells us the initial value of y when x is 0. For example, if the y-intercept is 3, it means that when x is 0, y is equal to 3. This point is often referred to as the starting point or the initial value. It helps us understand the relationship between x and y in the context of the problem.
Furthermore, the y-intercept can also tell us the vertical shift of the graph. If the y-intercept is positive, the graph will be shifted vertically upwards. If the y-intercept is negative, the graph will be shifted vertically downwards. By analyzing the y-intercept, we can gain insights into the behavior of the line and make predictions about its graph.
In summary, the y-intercept provides important information about the linear equation and its graph. It gives us the initial value of y when x is 0, helps us understand the relationship between x and y, and indicates the vertical shift of the graph. By interpreting the y-intercept, we can gain a deeper understanding of the equation and make meaningful interpretations in real-world scenarios.
Finding the y-Intercept Using the Slope-Intercept Form
In algebra, the slope-intercept form of a linear equation is represented as y = mx + b, where m represents the slope of the line and b represents the y-intercept. The y-intercept is the point where the line crosses the y-axis.
To find the y-intercept using the slope-intercept form, we can simply look at the equation and identify the value for b. The y-intercept is always represented as a single number or a constant term in the equation. For example, in the equation y = 2x + 3, the y-intercept is 3.
When graphing a linear equation, it is helpful to know the y-intercept because it allows us to easily plot a point on the y-axis. By starting at the y-intercept and using the slope, we can determine the direction in which the line is moving and plot additional points to accurately draw the line.
An alternative method to find the y-intercept is to set x equal to 0 in the slope-intercept form equation and solve for y. This will give us the y-coordinate of the y-intercept. For example, in the equation y = -0.5x + 2, when we substitute x = 0 into the equation, we find that y = 2. Therefore, the y-intercept is at the point (0, 2).
Practicing with Examples and Exercises
In order to become proficient in solving linear equations using the slope-intercept form, it is essential to practice with examples and exercises. This will help solidify your understanding of the concept and improve your ability to apply it in various scenarios.
Start by reviewing the basic formula of the slope-intercept form: y = mx + b. The “m” represents the slope of the line, while the “b” represents the y-intercept. Understanding the significance of these components will enable you to accurately graph equations and determine the characteristics of the line.
Next, work through a variety of examples that involve converting equations into slope-intercept form and identifying the slope and y-intercept. This will help reinforce your knowledge of the process and build your confidence. As you progress, challenge yourself with more complex equations and scenarios to further enhance your skills.
Once you feel comfortable with solving problems individually, try tackling some exercises that involve multiple equations. This will require you to apply your understanding of the slope-intercept form in a real-world context, such as finding the intersection point of two lines or determining the equation of a line passing through a specific point. These types of exercises will strengthen your problem-solving abilities and improve your overall comprehension of the topic.
Remember, consistent practice is key when it comes to mastering the slope-intercept form. Make use of various resources such as textbooks, online tutorials, and worksheets to supplement your learning. With dedication and regular practice, you will become proficient in solving linear equations using the slope-intercept form.
Understanding the Connection between Slope and Graphs
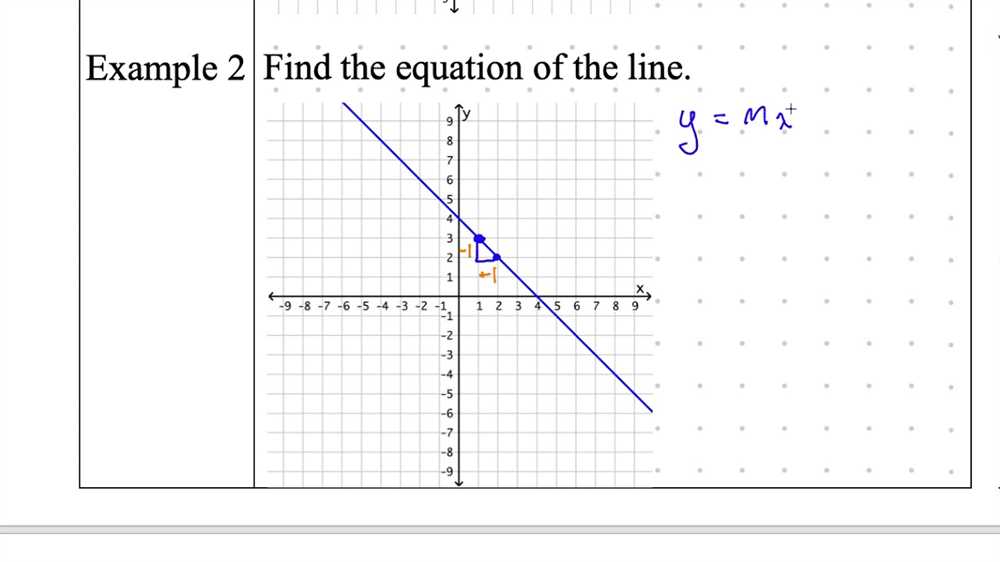
In mathematics, the concept of slope is closely connected to the graphs of linear equations. A linear equation represents a straight line on a graph, and the slope of that line determines its steepness and direction. The slope-intercept form of a linear equation, y = mx + b, helps us understand this connection.
In the slope-intercept form, m represents the slope of the line, and b represents the y-intercept, the point where the line intersects the y-axis. The slope, m, determines how the line moves vertically and horizontally on the graph. A positive slope indicates that the line is increasing as you move from left to right, while a negative slope indicates the line is decreasing.
To find the slope of a line, we can use the rise-over-run method. This involves selecting two points on the line and determining the change in y-values (the rise) and the change in x-values (the run) between those points. The slope is then calculated by dividing the rise by the run. A steeper line will have a larger rise and a smaller run, resulting in a larger slope.
Graphically, the slope is represented as the ratio of the vertical change to the horizontal change between any two points on the line. This allows us to visualize how the line is tilted and determine its steepness. By understanding the connection between slope and graphs, we can analyze linear equations and interpret their meanings in real-world contexts.
Key Points:

- The slope of a line determines its steepness and direction on a graph.
- The slope-intercept form of a linear equation, y = mx + b, helps us understand the connection between slope and graphs.
- Positive slope indicates an increasing line, while negative slope indicates a decreasing line.
- The rise-over-run method is used to find the slope by calculating the ratio of the vertical change to the horizontal change between two points on the line.
- Graphically, the slope represents the tilt and steepness of the line.