Understanding the concepts of perpendicular and angle bisectors is essential for solving geometry problems. Whether it’s determining the point of intersection between two lines or finding the measure of an angle, these concepts play a crucial role in geometry. In this article, we will provide an answer key to help you navigate through the complexities of perpendicular and angle bisectors.
The answer key will provide step-by-step explanations to common questions related to perpendicular and angle bisectors. It will cover topics such as finding the equations of perpendicular lines, identifying the point of intersection between two lines, and determining the measure of an angle. Each answer will be accompanied by a detailed explanation, ensuring that you not only find the correct solution but also understand the underlying concepts.
Whether you’re a student preparing for a geometry test or a teacher looking for additional resources to supplement your lessons, this answer key will be a valuable tool. It will serve as a comprehensive guide, offering clear explanations and examples for each topic. By following along with the answer key, you’ll be able to strengthen your understanding of perpendicular and angle bisectors and confidently tackle geometry problems.
So, if you’re ready to enhance your knowledge of perpendicular and angle bisectors, dive into this answer key. From finding the equations of perpendicular lines to solving complex angle problems, this guide will equip you with the skills and knowledge necessary to excel in geometry. Let’s get started!
Definition and Properties of Perpendicular Bisectors
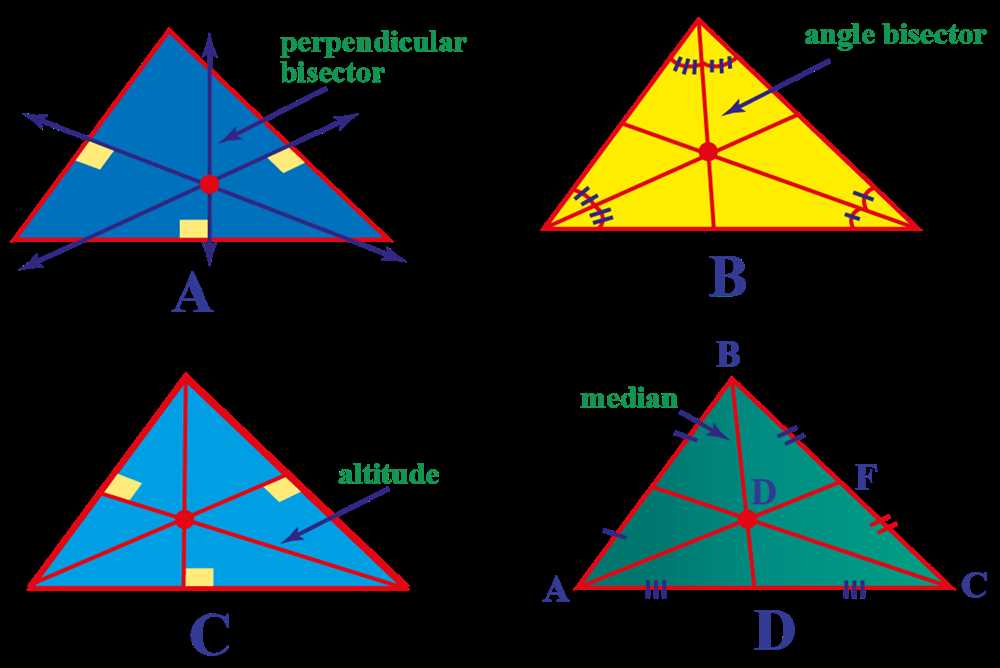
A perpendicular bisector is a line or a segment that divides another line or segment into two equal parts at a right angle. It is called a perpendicular bisector because it is both perpendicular (forming a 90-degree angle) to the line or segment being bisected and bisects it into two equal parts.
One key property of a perpendicular bisector is that it is equidistant from the endpoints of the line or segment being bisected. This means that the distance from any point on the perpendicular bisector to one of the endpoints is equal to the distance from that same point to the other endpoint. This property can be used to construct a perpendicular bisector using compass and straightedge.
Another important property of perpendicular bisectors is that they intersect at a point called the circumcenter. The circumcenter is the center of the circumcircle, which is a circle that passes through all three vertices of a triangle. In other words, the perpendicular bisectors of the sides of a triangle intersect at a single point, the circumcenter.
The perpendicular bisectors of a triangle also have the property of being the lines of symmetry for the triangle. This means that if you fold the triangle along one of its perpendicular bisectors, the two halves will match up exactly. Furthermore, the angles formed by the intersection of the perpendicular bisectors are all congruent.
In summary, perpendicular bisectors are lines or segments that divide other lines or segments into two equal parts at right angles. They have the properties of being equidistant from the endpoints of the line or segment being bisected, intersecting at the circumcenter, and serving as lines of symmetry for triangles.
Definition and Properties of Angle Bisectors
An angle bisector is a line or ray that divides an angle into two congruent angles. It is a line or ray that starts at the vertex of the angle and extends to the opposite side of the angle.
When an angle is bisected, it creates two smaller angles that have the same measure. Let’s say we have an angle ABC. If we bisect it with a line or ray AD, we will have two angles: angle ADB and angle BDC. These two angles will be congruent, meaning they will have the same measure.
A key property of an angle bisector is that it divides the opposite side into two segments that are proportional to the adjacent sides of the angle. In the case of triangle ABC, if AD is the angle bisector of angle BAC, then AB/BD = AC/CD.
Another property of angle bisectors is that they are perpendicular to the opposite side. In the case of triangle ABC, line AD, the angle bisector of angle BAC, will be perpendicular to the side BC.
Angle bisectors are important in many geometric proofs and constructions. They help us divide angles and find proportional segments within triangles. Understanding their properties allows us to solve various problems involving angles and triangle congruence.
Solving Perpendicular Bisector Problems
The concept of perpendicular bisectors plays an important role in geometry and is often used in solving various mathematical problems. A perpendicular bisector is a line that divides a segment into two equal parts at a right angle. It can be used to determine the midpoint of a line segment and to construct right angles. Solving perpendicular bisector problems involves analyzing the given information and applying the properties and theorems related to perpendicular bisectors.
When solving perpendicular bisector problems, it is important to first identify the given information and understand the question or problem statement. This may involve identifying the points or lines involved, the lengths of the segments, or the angles formed. Once the given information is clear, the properties and theorems related to perpendicular bisectors can be applied.
- One common problem involves finding the equation of a perpendicular bisector. To solve this problem, the coordinates of the endpoints of the line segment are needed. The midpoint of the segment can be found using the midpoint formula, and the slope of the segment can be found using the slope formula. The negative reciprocal of the slope is then used to find the slope of the perpendicular bisector. Finally, the equation of the perpendicular bisector is determined using the midpoint formula and the slope-intercept form.
- Another problem involves determining if a point lies on the perpendicular bisector of a line segment. In this case, the coordinates of the point and the endpoints of the segment are required. The equation of the perpendicular bisector can be found using the same method as mentioned above. Substituting the coordinates of the point into the equation of the perpendicular bisector can then determine if the point lies on the line.
By understanding the properties and theorems related to perpendicular bisectors and applying them to solve various problems, one can develop a deeper understanding of geometry and enhance their problem-solving skills.
Finding Equations of Perpendicular Bisectors
A perpendicular bisector is a line that cuts another line segment into two equal halves and forms a right angle with it. This means that the perpendicular bisector is equidistant from the endpoints of the line segment. Finding the equation of a perpendicular bisector involves determining its slope and finding its y-intercept.
To find the equation of a perpendicular bisector, we first need to find the slope of the line segment. The slope of a line is given by the formula: m = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are the coordinates of the two endpoints of the line segment. Once we have the slope of the line segment, we can find the negative reciprocal of it to get the slope of the perpendicular bisector. For example, if the slope of the line segment is 2, the slope of the perpendicular bisector would be -1/2.
After finding the slope of the perpendicular bisector, we can use the midpoint formula to find its coordinates. The midpoint formula is given by: (x, y) = ((x1 + x2) / 2, (y1 + y2) / 2), where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment. The coordinates of the midpoint will be the x-intercept and y-intercept of the perpendicular bisector.
Finally, we can use the slope-intercept form of a line, y = mx + b, to find the equation of the perpendicular bisector. We substitute the slope and the coordinates of the midpoint into the equation and solve for b, the y-intercept. The equation will then be in the form y = mx + b, where m is the slope of the perpendicular bisector and b is the y-intercept.
In summary, finding the equation of a perpendicular bisector involves finding the slope of the line segment, finding the negative reciprocal of the slope to get the slope of the perpendicular bisector, finding the coordinates of the midpoint, and using the slope-intercept form of a line to find the equation. This process allows us to determine the equation of a line that cuts a line segment into two equal halves and forms a right angle with it.
Determining Intersection Points of Perpendicular Bisectors

A perpendicular bisector is a line that intersects a line segment at a 90-degree angle and divides it into two equal parts. When given two line segments, we can determine their intersection point by finding the perpendicular bisectors of each segment and identifying where they intersect.
To find the intersection point, we first need to find the equations of the perpendicular bisectors. The equation of a perpendicular bisector can be determined using the midpoint formula and the negative reciprocal of the slope of the line segment.
For example, let’s say we have two line segments AB and CD. To find the intersection point, we first find the midpoint of AB using the midpoint formula. Then, we calculate the slope of AB and find its negative reciprocal, which will be the slope of the perpendicular bisector. We repeat this process for the line segment CD.
Once we have the equations of the perpendicular bisectors, we can solve the system of equations to find the intersection point. We substitute one equation into the other and solve for the variables. The resulting values will give us the coordinates of the intersection point.
It’s important to note that in some cases, the two line segments may not intersect, and the equations of the perpendicular bisectors may not have a solution. In these cases, the line segments are parallel or do not intersect at all.
In conclusion, determining the intersection points of perpendicular bisectors involves finding the equations of the bisectors and solving the system of equations. This process allows us to find the coordinates where the line segments intersect and divide them into two equal parts.
Solving Angle Bisector Problems
An angle bisector is a line that divides an angle into two equal parts. Solving angle bisector problems involves applying geometric principles and concepts to find missing angles and lengths.
To solve angle bisector problems, it is important to understand the properties and theorems related to angles and their bisectors. One important theorem is the Angle Bisector Theorem, which states that in a triangle, the angle bisector of an angle divides the opposite side into segments that are proportional to the other two sides of the triangle. This theorem can be used to find missing side lengths or angles in a triangle.
- To solve an angle bisector problem, start by identifying the given information, such as the lengths of sides or the measures of angles in the triangle.
- Then, apply the Angle Bisector Theorem or other relevant theorems to set up an equation or proportion that relates the known and unknown quantities.
- Solve the equation or proportion to find the value of the unknown quantity.
- Check your solution by substituting the found value back into the original equation or proportion to ensure that both sides are equal.
Example:
In a triangle ABC, angle A is bisected by line AD. If the measure of angle A is 60 degrees and the length of side AB is 8 inches, find the length of side AD.
Solution:
- Given: angle A is 60 degrees, length of AB is 8 inches.
- By the Angle Bisector Theorem, the ratio of the length of segment BD to the length of segment DC is equal to the ratio of the length of side AB to the length of side AC.
- Let x be the length of segment BD and y be the length of segment DC.
- Setting up the proportion: x/y = AB/AC.
- Substituting the given values: x/y = 8/AC.
- Simplifying the proportion: x/y = 8/AC.
- Multiplying both sides by AC: x = 8(AC/y).
- Since AD is the sum of segment BD and segment DC, AD = x + y.
- Substituting the found value of x: AD = 8(AC/y) + y.
- Simplifying further: AD = (8AC + y^2)/y.
- Unfortunately, we don’t have enough information to solve for the length of AD with the given values. We would need additional information such as the length of side AC or the angle measures of the triangle.
Finding Equations of Angle Bisectors

The concept of angle bisectors plays an important role in geometry and trigonometry. An angle bisector is a line or ray that divides an angle into two congruent angles. To find the equation of an angle bisector, we can use various methods and formulas.
One method to find the equation of an angle bisector is by using the slope-intercept form of a line. Given the equation of the two lines forming the angle, we can first find the slopes of these lines using the formula (y2 – y1) / (x2 – x1). Then, we can find the average of these slopes to determine the slope of the angle bisector. Next, we need to find a point on the angle bisector. We can do this by finding the intersection point of the two lines. Finally, we can use the slope-intercept form (y = mx + b) with the slope and the point to find the equation of the angle bisector.
Another method to find the equation of an angle bisector is by using the distance formula. Given the coordinates of the vertices of the angle, we can first find the distances between these points. Then, we can use the properties of angle bisectors to find the lengths of the segments created by the angle bisector. Finally, we can use the distance formula again to find the coordinates of a point on the angle bisector. With this point and the slope of the angle bisector, we can find the equation of the line using the point-slope form (y – y1 = m(x – x1)).
In conclusion, finding the equations of angle bisectors involves determining the slopes and points on the bisectors using various techniques such as the slope-intercept form and the distance formula. These equations help us analyze and understand the properties of angles and their bisectors in geometric and trigonometric problems.
Solving for Missing Angles using Angle Bisectors

When confronted with a geometry problem that involves angles, finding the measures of missing angles can be a challenging task. However, one helpful tool in solving for missing angles is the use of angle bisectors. An angle bisector is a line or ray that divides an angle into two congruent angles. By knowing the properties of angle bisectors, we can apply them to find the measures of unknown angles.
One key property of angle bisectors is that they divide the opposite side of the angle into segments that are proportional to the adjacent sides. This property allows us to set up equations and solve for missing angles. For example, if we have a triangle where an angle bisector divides the opposite side into segments of length x and y, and we know the lengths of the adjacent sides, we can use similar triangles to set up the equation:
- x / a = y / b
Where a and b are the lengths of the adjacent sides. By cross-multiplying and solving for x or y, we can find the length of the segment divided by the angle bisector, which gives us the measure of the missing angle.
In addition to using angle bisectors to find missing angles, they can also be used to prove theorems and solve more complex geometry problems. By recognizing the properties of angle bisectors, such as dividing an angle into congruent angles and segment proportionality, we can apply these concepts to various geometric scenarios.