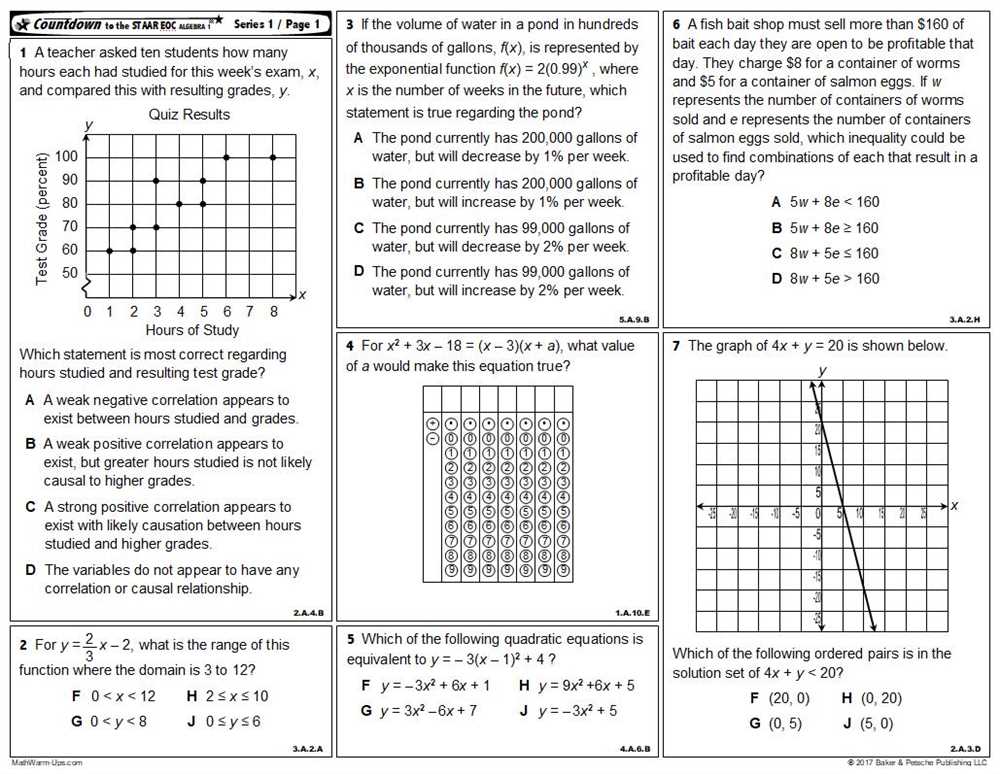
In mathematics, linear functions are essential in modeling real-world situations and analyzing various relationships between variables. To understand linear functions thoroughly, it is important to have a strong grasp of their key concepts and properties.
In this article, we will provide you with the answer key to the exercises in Section 5.1, which focuses on understanding linear functions. By referring to this answer key, you will be able to check your solutions and enhance your understanding of linear functions even further.
Section 5.1 covers a range of topics, including slope, intercepts, graphing linear functions, and finding equations from given information. By correctly solving the exercises in this section, you will gain proficiency in these fundamental aspects of linear functions.
Whether you are a student studying algebra or a professional in a field that requires mathematical analysis, having a solid understanding of linear functions is crucial. By consulting the answer key provided here, you can clarify any doubts or misconceptions you may have and build a strong foundation in this fundamental area of mathematics.
Understanding Linear Functions Answer Key: 5 Essential Concepts
In order to understand linear functions, it is important to grasp five essential concepts. These concepts serve as the foundation for working with linear functions and are crucial for solving related problems and equations. By mastering these concepts, one can confidently navigate through linear functions and their applications.
1. Linearity
Linearity is at the core of linear functions. It refers to the property of a function that exhibits a straight line relationship between the input and output values. In other words, a function is linear if it can be graphed as a straight line. This concept allows for the simplification and understanding of complex relationships in a straightforward manner.
2. Slope
The slope of a linear function determines the rate of change between two points on the graph. It represents the steepness of the line and is found by calculating the ratio of the vertical change (rise) to the horizontal change (run). The slope is a fundamental concept in understanding the behavior of linear functions and is often used to analyze real-world situations and make predictions.
3. Y-Intercept
The y-intercept is the point where the line of a linear function intersects the y-axis. It is represented by the coordinate (0, b) and indicates the initial value or starting point of the function. The y-intercept provides important information about the function’s behavior and allows for easy interpretation of the graph.
4. Linear Equations
Linear equations provide a concise way of representing linear functions algebraically. They are written in the form y = mx + b, where m represents the slope and b represents the y-intercept. Solving linear equations involves manipulating the variables to find specific values or relationships between them.
5. Graphing
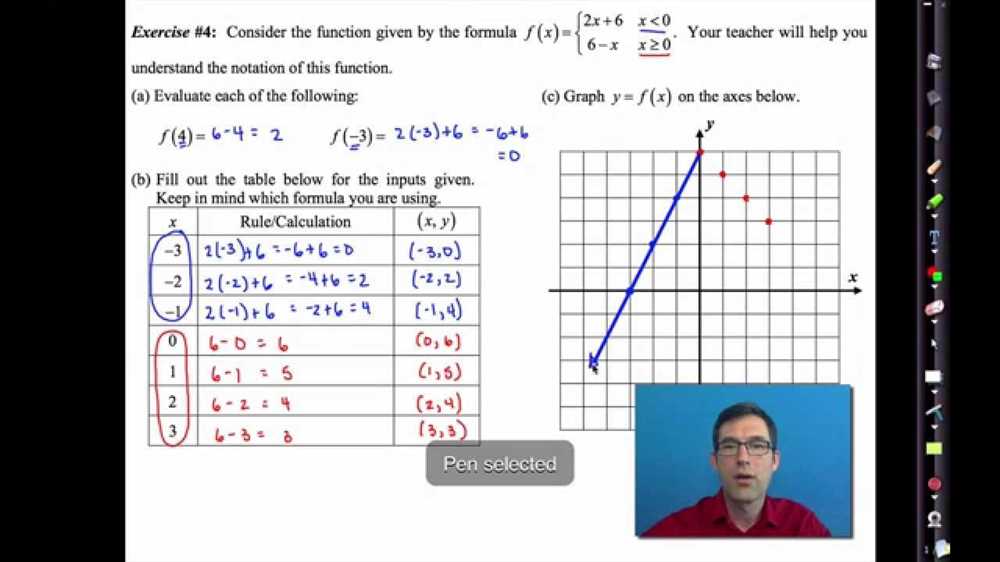
Graphing linear functions is an important skill for visualizing and analyzing their behavior. By plotting points or using the slope and y-intercept, one can accurately represent the linear relationship between the input and output values. Graphs provide a visual representation of the function and can aid in understanding its properties and applications.
Definition of Linear Functions

Linear functions are mathematical functions that can be represented by a straight line on a graph. They are commonly used to model relationships between two variables, where the dependent variable is a constant rate of change with respect to the independent variable. The general form of a linear function is y = mx + b, where m is the slope of the line and b is the y-intercept, the point where the line crosses the y-axis.
The slope of a linear function measures the rate at which the dependent variable changes with respect to the independent variable. It represents the vertical change (rise) divided by the horizontal change (run) between any two points on the line. A positive slope indicates an increasing relationship, where the dependent variable increases as the independent variable increases. A negative slope indicates a decreasing relationship, where the dependent variable decreases as the independent variable increases.
Linear functions are characterized by their constant rate of change, meaning that for every unit increase in the independent variable, the dependent variable changes by a constant amount. This property makes linear functions useful in many real-world situations, such as calculating distances, determining rates of change, and predicting future values. They are also fundamental in algebraic concepts, as they provide a basis for understanding more complex functions and equations.
Characteristics of Linear Functions
A linear function is a function that can be represented by a straight line on a graph. It is one of the most fundamental types of functions in mathematics, and it has several key characteristics that distinguish it from other types of functions.
1. Constant rate of change
One of the main characteristics of a linear function is that it has a constant rate of change. This means that for every unit increase in the independent variable, the dependent variable will increase or decrease by the same amount. In other words, the slope of a linear function remains constant throughout its domain.
2. Straight line graph
As mentioned earlier, the graph of a linear function is a straight line. This is because the constant rate of change corresponds to a constant slope, which determines the angle at which the line intersects the x-axis. The equation of a linear function can be written in the form y = mx + b, where m represents the slope and b represents the y-intercept.
3. No exponential growth or decay
Unlike exponential functions, linear functions do not exhibit exponential growth or decay. This means that the dependent variable increases or decreases at a constant rate, rather than at an increasing or decreasing rate. The straight line nature of a linear function reflects this constant rate of change.
4. One-to-one correspondence
A linear function has a one-to-one correspondence between its domain and range. This means that each input value corresponds to a unique output value, and vice versa. There are no repeated x-values or y-values in a linear function, which is another characteristic that sets it apart from other types of functions.
In conclusion, linear functions have several distinctive characteristics, including a constant rate of change, a straight line graph, no exponential growth or decay, and a one-to-one correspondence between their domain and range. These characteristics make linear functions an important concept in mathematics and are fundamental to understanding various applications in real-life situations.
Graphing Linear Functions
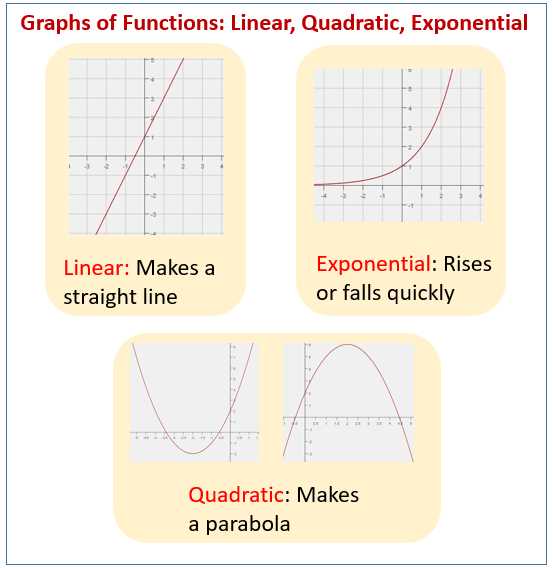
A linear function is a mathematical equation that represents a straight line on a graph. It is written in the form of y = mx + b, where m is the slope of the line and b is the y-intercept. Graphing linear functions allows us to visually represent the relationship between two variables and analyze their behavior.
To graph a linear function, we need to plot a few points on the coordinate plane and then connect them with a straight line. The slope of the line determines its steepness, while the y-intercept tells us where it crosses the y-axis. By knowing these two pieces of information, we can easily graph the linear function.
One way to graph a linear function is by creating a table of values. We choose different x-values and substitute them into the equation to find the corresponding y-values. These points can then be plotted on the graph. By connecting the points, we can see the line representing the linear function.
Another way to graph a linear function is by using the slope-intercept form. This form directly gives us the slope and y-intercept of the line. We start by plotting the y-intercept on the graph, and then use the slope to find additional points to plot. By connecting these points, we can accurately graph the linear function.
Graphing linear functions is an essential skill in understanding the behavior of many real-world phenomena. By visualizing the relationship between variables, we can make predictions, determine trends, and solve problems in various fields such as economics, physics, and engineering.
Finding Slope and Y-Intercept
Understanding linear functions involves being able to find the slope and y-intercept of a given equation. The slope is a measure of how steep the line is, while the y-intercept indicates where the line crosses the y-axis. By identifying these two values, we can gain insights into the behavior and characteristics of the linear function.
To find the slope of a linear function, we need two points on the line. We can then use the formula: slope = (change in y) / (change in x). This formula calculates the ratio of the vertical change to the horizontal change between the two points. The resulting value represents the slope of the line. A positive slope indicates the line is increasing from left to right, while a negative slope shows a decreasing pattern.
The y-intercept of a linear function is the point at which the line crosses the y-axis. It is represented by the coordinate (0, b), where b is the value of y when x is 0. To find the y-intercept, we can either directly read it from the equation (if it is in slope-intercept form y = mx + b) or substitute x = 0 into the equation and solve for y.
In summary, understanding linear functions involves finding the slope and y-intercept. The slope indicates the steepness of the line, while the y-intercept shows where the line intersects the y-axis. By calculating or identifying these values, we can gain insights into the behavior and characteristics of the linear function.
Solving Equations with Linear Functions
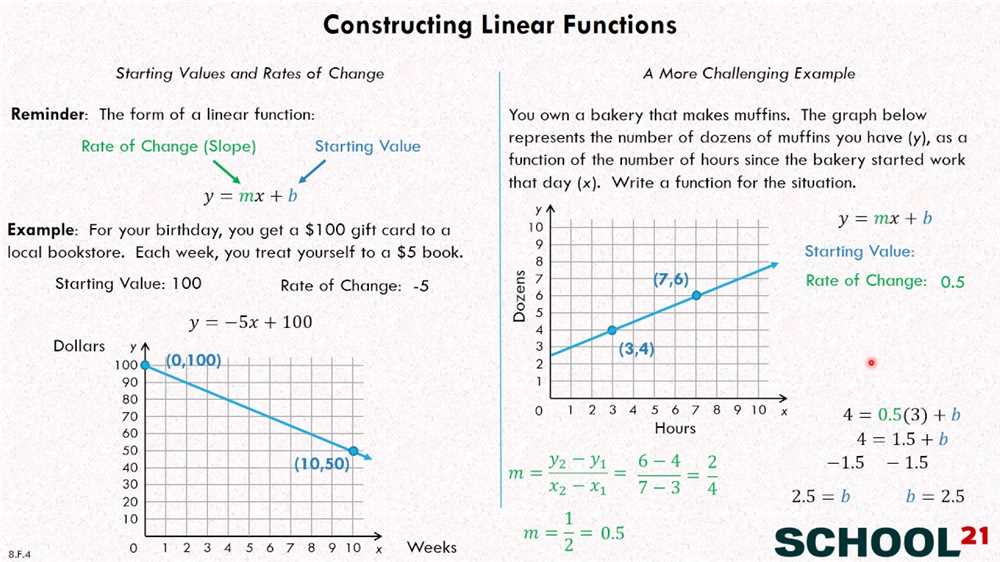
Linear functions are an essential tool in solving equations, as they represent a straight line on a graph. By understanding the properties of linear functions, we can use them to find solutions to equations involving variables.
One of the key concepts in solving equations with linear functions is the slope-intercept form, which is given by y = mx + b. Here, m represents the slope of the line, and b represents the y-intercept, which is the value of y when x is equal to 0. By rearranging the equation and substituting values, we can solve for both x and y.
When given an equation involving a linear function, we can follow a step-by-step process to find the solutions. First, we identify the slope and y-intercept of the line. Then, we can plot the y-intercept on a graph and use the slope to determine the direction and steepness of the line. This helps us visualize the relationship between the variables and better understand the equation.
Once we have the graph, we can find the solutions to the equation by identifying the points where the line intersects the x-axis or y-axis. These points represent the solutions to the equation, as they satisfy the equality between x and y.
By using linear functions and their properties, we can effectively solve equations involving variables. This allows us to find the specific values of the variables that satisfy the equation and understand the relationship between them.
Understanding the Standard Form of Linear Equations
Linear equations are an important concept in algebra that help us describe and study the relationship between variables. One common way to represent these equations is in standard form, which is written as Ax + By = C, where A, B, and C are constants. Understanding the standard form of linear equations is crucial for solving real-life problems and graphing these equations.
In the standard form, A, B, and C represent the coefficients of the equation. The coefficient A stands for the x-term, coefficient B represents the y-term, and C is the constant term. By arranging the equation in this form, it becomes easier to identify the slope and y-intercept of the line.
In order to graph a linear equation in standard form, one can follow a few simple steps. First, one can find the x-intercept by setting y to 0 and solving for x. This gives the coordinates (x, 0) of the x-intercept. Next, one can find the y-intercept by setting x to 0 and solving for y. This gives the coordinates (0, y) of the y-intercept. Plotting these two points and connecting them with a straight line will give the graph of the linear equation.
Furthermore, the standard form of linear equations allows us to easily manipulate and solve them. By rearranging the terms, one can solve for x or y, or even convert the equation into slope-intercept form (y = mx + b), where m represents the slope of the line and b represents the y-intercept. This flexibility and simplicity make the standard form of linear equations a powerful tool in algebra and beyond.
Applications of Linear Functions in Real Life
In real life, linear functions are widely used in various applications to model and solve problems. One common application is in the field of finance and economics, where linear functions can be used to predict and analyze trends in the stock market, calculate interest rates for loans and investments, and determine the optimal pricing strategy for a product or service.
For example, a company may use a linear function to determine the relationship between the price of a product and the demand for that product. By studying historical data and performing regression analysis, the company can determine the slope and y-intercept of the linear function, which represent the rate of change in demand and the initial demand, respectively. This information can then be used to optimize pricing and maximize profits.
In addition to finance and economics, linear functions are also used in the field of engineering. For instance, civil engineers may use linear functions to model the relationship between the length of a bridge and the amount of weight it can support. By analyzing the data and determining the slope and y-intercept, engineers can design bridges that are safe and reliable.
Linear functions are also used in transportation planning, as they can be used to model the relationship between speed and distance. By analyzing data on travel times and distances, transportation planners can determine the optimal speed limit for a road or the most efficient route for a delivery truck.
Overall, linear functions play a crucial role in many real-life applications, from finance to engineering to transportation planning. By understanding and utilizing linear functions, individuals and organizations can make informed decisions and solve complex problems.