
Linear relationships play a crucial role in various fields such as mathematics, physics, economics, and more. Understanding how to model these relationships and finding the answer key to solve related problems is essential for success in these disciplines. In this article, we will delve into the concept of modeling linear relationships and explore the answer key to help you enhance your skills in this area.
Modeling linear relationships involves representing the relationship between two variables using a straight line on a graph. This powerful tool allows us to analyze and predict how one variable changes in response to changes in another. By finding the answer key to these relationships, we can gain insights into the relationship’s slope, y-intercept, and equation.
Through modeling linear relationships, we can interpret real-world scenarios and make predictions based on the given data. This skill is essential in fields such as economics, where we can analyze how changes in one variable, such as price, affect another variable, such as demand. By understanding the answer key to these relationships, we can optimize business strategies, forecast market trends, and make informed decisions.
In this article, we will explore various methods to model linear relationships, including graphing, slope-intercept form, and point-slope form. We will also discuss how to find the answer key by solving systems of linear equations, applying regression analysis, and using technology tools like calculators or computer software. By mastering these techniques, you will be equipped to tackle complex problems and deepen your understanding of linear relationships.
So, whether you are a student studying mathematics, a scientist analyzing experimental data, or a business professional making data-driven decisions, understanding how to model linear relationships and uncover the answer key is a crucial skill. Join us on this exploration of modeling linear relationships to enhance your knowledge and increase your problem-solving abilities.
1 Modeling Linear Relationships Answer Key
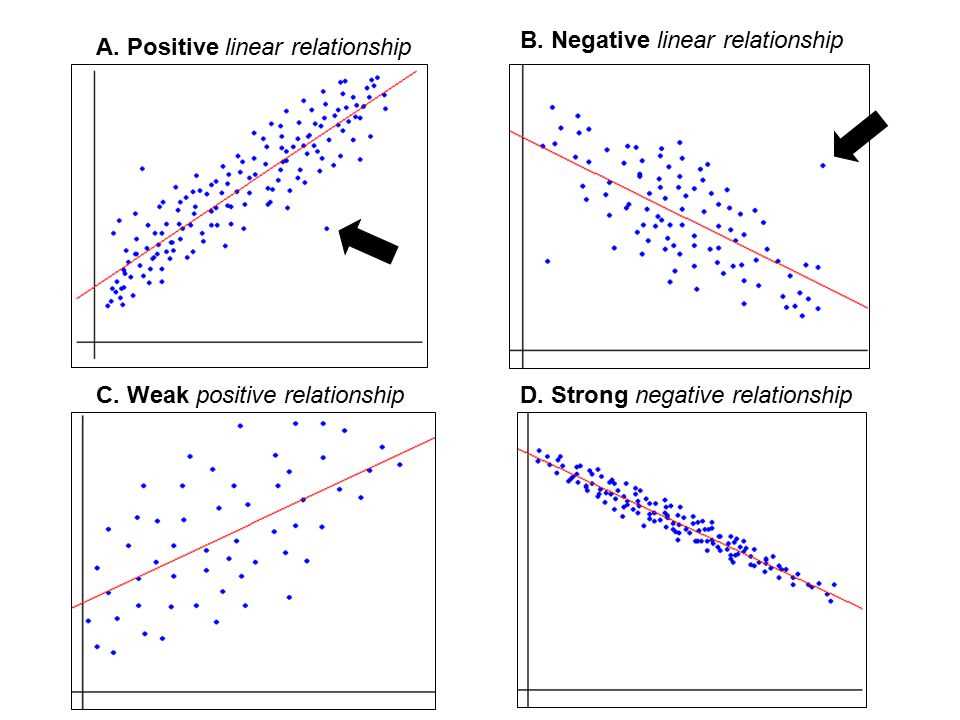
When it comes to modeling linear relationships, having an answer key can be extremely helpful. It allows us to compare our own work with the correct solutions and identify any mistakes or areas for improvement. This answer key for modeling linear relationships provides us with the solutions to various problems and exercises relating to this topic.
One of the main benefits of using an answer key is that it allows us to check our work for accuracy. By comparing our solutions to the correct answers provided in the answer key, we can identify any errors or misconceptions we may have had. This helps us to better understand the concept of modeling linear relationships and improve our skills in solving related problems.
The answer key typically includes step-by-step solutions to each problem, clarifying the thought process and reasoning behind each step. This can be incredibly beneficial, as it allows us to see how the problem can be approached and solved systematically. By understanding the logic behind the solution, we can apply it to similar problems in the future.
Using an answer key also allows us to practice and reinforce our understanding of the concept. By attempting the problems on our own and then checking our work against the answer key, we can identify any areas of weakness and focus on improving those specific skills. This iterative process of practice and review helps us to develop a deeper understanding of modeling linear relationships.
Overall, having an answer key for modeling linear relationships is a valuable resource that can enhance our learning and problem-solving abilities. It provides us with guidance, allows us to identify and correct mistakes, and reinforces our understanding of the concept. By utilizing an answer key, we can improve our skills in modeling linear relationships and apply them to real-world scenarios.
Section 1: Understanding Linear Relationships
Linear relationships play a fundamental role in the field of mathematics and are widely used in various disciplines such as physics, economics, and engineering. In this section, we will explore the concept of linear relationships and the tools needed to understand and model them.
A linear relationship is a mathematical relationship between two variables that can be represented by a straight line on a graph. One variable is typically considered the independent variable, while the other is the dependent variable. The independent variable is the cause or input, while the dependent variable is the effect or output. The equation of a linear relationship is of the form y = mx + b, where y represents the value of the dependent variable, x represents the value of the independent variable, m represents the slope of the line, and b represents the y-intercept.
To understand linear relationships, it is crucial to have a good grasp of slope and y-intercept. The slope of a line measures its steepness and is calculated as the change in y divided by the change in x. It represents the rate of change of the dependent variable with respect to the independent variable. The y-intercept, on the other hand, is the point where the line intersects the y-axis. It indicates the initial value of the dependent variable when the independent variable is zero.
Graphing is a powerful tool to visualize and analyze linear relationships. By plotting sets of data points on a graph, we can identify patterns and trends. These patterns can help us determine the slope and y-intercept, as well as make predictions about the dependent variable for different values of the independent variable.
Understanding linear relationships is essential for solving real-world problems and making informed decisions. Whether it’s forecasting future sales based on historical data or optimizing production processes, the ability to model and analyze linear relationships provides valuable insights and helps us make more accurate predictions.
In the next sections, we will delve deeper into the intricacies of linear relationships and explore various techniques for modeling and analyzing them. We will discuss methods for finding equations of lines, interpreting slope and y-intercept, and using regression analysis to make predictions. Through practical examples and exercises, we will develop a strong understanding of linear relationships and their applications in the real world.
Section 2: Identifying Linear Equations
A linear equation is an equation that represents a straight line on a graph. It can be written in the form y = mx + b, where m is the slope and b is the y-intercept. In this section, we will learn how to identify linear equations based on their characteristics and representations.
One way to identify a linear equation is by looking at its graph. If the graph of an equation is a straight line, then it is a linear equation. The slope of the line can be determined by observing the steepness of the line and the direction it is moving in. The y-intercept can be found by determining the point where the line crosses the y-axis.
Another way to identify a linear equation is by examining its algebraic representation. If an equation can be rearranged into the form y = mx + b, where the variables are raised to the power of 1 and there are no terms with higher powers, then it is a linear equation. The coefficient of x represents the slope, while the constant term represents the y-intercept.
When identifying linear equations, it is important to note that not all equations with two variables are linear. Some equations may be quadratic, exponential, or even non-linear. Therefore, it is crucial to analyze the characteristics and representations of an equation to determine if it is indeed linear.
- A linear equation can be identified by its graph, which is a straight line.
- A linear equation can also be identified by its algebraic representation, which is in the form y = mx + b.
- It is important to distinguish linear equations from other types of equations, such as quadratic or exponential equations.
Section 3: Solving Linear Equations

In this section, we will focus on solving linear equations. Linear equations are algebraic expressions in which the variables are raised to the power of one. Solving linear equations involves finding the value of the variable that makes the equation true.
One of the main methods used to solve linear equations is the balance method. This method involves maintaining the equality of the equation by performing the same operation on both sides of the equation. By doing so, we can isolate the variable and determine its value.
To solve a linear equation, it is important to follow a step-by-step approach. First, simplify both sides of the equation by combining like terms. Then, get rid of any constants or coefficients by performing inverse operations. After that, isolate the variable by moving all other terms to the opposite side of the equation. Finally, solve for the variable by performing any necessary operations.
When solving linear equations, it is crucial to keep track of the operations performed on both sides of the equation. This helps ensure that we maintain the equality of the equation throughout the solving process. Additionally, it is important to check the solution obtained by substituting the value back into the original equation to verify its accuracy.
By following these steps and applying the balance method, we can effectively solve linear equations and find the value of the variable. Solving linear equations is an important skill that is used in various fields, such as science, engineering, and finance, to analyze and solve real-world problems.
Section 4: Graphing Linear Equations
A linear equation represents a straight line on a graph. Graphing linear equations is an important skill in mathematics as it helps us visualize the relationship between variables and understand their behavior. In this section, we will learn how to graph linear equations using various methods and techniques.
One method to graph a linear equation is to use the slope-intercept form, which is in the form y = mx + b. The slope, represented by the variable m, indicates how steep the line is, while the y-intercept, represented by the variable b, gives us the point where the line crosses the y-axis. By using the slope and y-intercept, we can plot the points and draw a straight line to represent the equation on a graph.
Another method to graph a linear equation is by using the x-intercept and y-intercept. The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis. By determining these intercepts, we can plot the points and draw a straight line to represent the equation on a graph.
Graphing linear equations allows us to visually analyze their properties, such as the slope, y-intercept, x-intercept, and whether the equation represents a positive or negative relationship between variables. It also helps us understand the solution to the equation, as the point where the line intersects the x-axis represents the x-coordinate of the solution, and the point where the line intersects the y-axis represents the y-coordinate of the solution.
Overall, graphing linear equations is an essential skill in mathematics that enables us to analyze and understand the relationships between variables. By visually representing equations on a graph, we can interpret their properties and find solutions more effectively.
Section 5: Finding the Slope of a Line
In mathematics, the slope of a line is a measure of how steep it is. It describes the rate of change between two points on the line. Finding the slope of a line is an important skill in algebra and is used in various problem-solving situations.
To find the slope of a line, we need to know the coordinates of two points on the line. Let’s consider the points (x1, y1) and (x2, y2). The formula to calculate the slope is:
Slope = (y2 – y1) / (x2 – x1)
This formula represents the change in y divided by the change in x between the two points. The result will be a numerical value that represents the slope of the line.
The slope can tell us many things about the line. If the slope is positive, it means that as x increases, y also increases, and the line is going upward. If the slope is negative, y decreases as x increases, and the line is going downward. A slope of zero means there is no change in y as x changes, and the line is horizontal.
Knowing how to find the slope of a line is crucial for understanding linear relationships and analyzing data in various fields such as economics, physics, and engineering. It helps us interpret the relationship between two variables and make predictions based on the given data.
Section 6: Interpreting the Slope and y-intercept
When working with linear relationships, it is important to understand the meaning behind the slope and y-intercept. The slope represents the rate of change between the variables in the relationship. It tells us how much the dependent variable (y) changes for every unit increase in the independent variable (x). The slope can be positive or negative, indicating whether the variables are positively or negatively related. A slope of zero indicates no relationship between the variables.
The y-intercept, on the other hand, represents the value of the dependent variable (y) when the independent variable (x) is equal to zero. It is the point where the line intersects the y-axis. The y-intercept is often interpreted as the starting value or initial condition of the relationship. It gives us an idea of where the line begins and helps us make predictions for values of the dependent variable when the independent variable is zero.
In practical terms, interpreting the slope and y-intercept can help us make predictions and understand the behavior of the relationship. For example, if the slope is positive, we know that as the independent variable increases, the dependent variable also increases at a certain rate. If the slope is negative, it means that as the independent variable increases, the dependent variable decreases. The magnitude of the slope tells us how steep the line is, indicating how large or small the change in the dependent variable is for each unit increase in the independent variable.
Similarly, the y-intercept gives us information about the initial value of the dependent variable. If the y-intercept is large, it means that even when the independent variable is zero, the dependent variable has a significant starting value. On the other hand, if the y-intercept is close to zero, it suggests that the initial value of the dependent variable is small.
Interpreting the slope and y-intercept allows us to understand the relationship between two variables and make predictions based on this understanding. By analyzing the rate of change and initial condition, we can better analyze and model linear relationships.