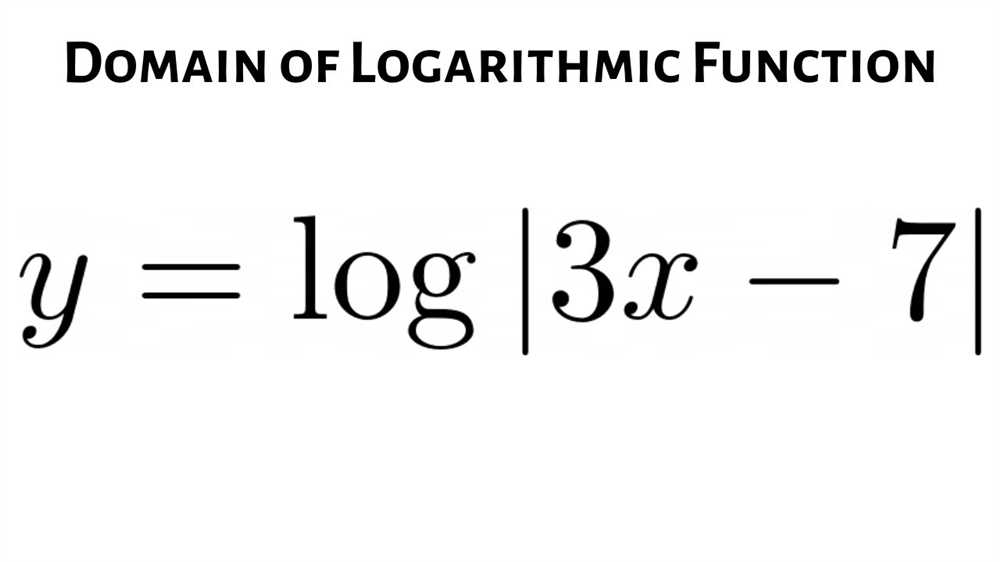
Logarithms and logarithmic functions are essential concepts in mathematics and play a crucial role in various fields such as engineering, physics, and data analysis. In this article, we will explore the answers to seven questions related to logarithms and logarithmic functions, providing a comprehensive understanding of these mathematical tools.
Firstly, we will delve into the definition and properties of logarithms, which are mathematical operations that allow us to solve equations involving exponents. We will explore the relationship between logarithms and exponential functions, understanding how they are inversely related and can be used to convert between different bases.
Next, we will address common misconceptions and difficulties that students often encounter when working with logarithmic functions. By clarifying these misconceptions and providing step-by-step explanations, we aim to facilitate a deeper understanding of logarithmic equations and their applications.
Furthermore, we will discuss the concept of logarithmic scales, which are widely used in scientific and engineering disciplines to represent data that spans a large range of values. We will explain how logarithmic scales provide a more intuitive way to interpret and analyze data, especially when dealing with exponential growth or decay.
In conclusion, this article will provide clear and concise answers to seven important questions related to logarithms and logarithmic functions. By understanding the fundamental concepts and applications of logarithms, readers will gain a solid foundation for further exploration in advanced mathematics and its practical applications in various fields.
Understanding logarithms and logarithmic functions
Logarithms and logarithmic functions are mathematical tools used to solve equations involving exponential growth or decay. They are a fundamental concept in algebra and have numerous applications in science, engineering, and finance. In this article, we will explore the basics of logarithms and logarithmic functions and their properties.
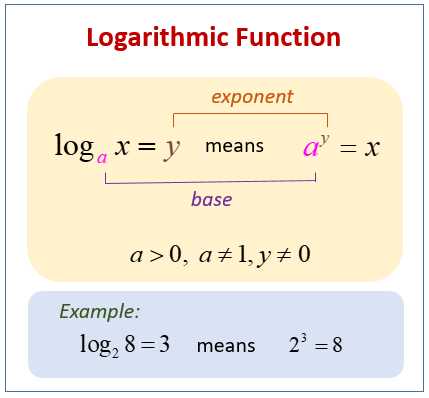
A logarithm is the inverse operation of exponentiation. It helps us answer the question: “What exponent do we need to raise a given base to in order to get a certain number?” Logarithms are denoted as logb(x), where b is the base and x is the number we want to find the exponent of. For example, log2(8) asks us “What exponent should we raise 2 to in order to get 8?” The answer is 3, because 23 = 8. Therefore, log2(8) = 3.
Logarithmic functions are functions that involve logarithms. They are written in the form f(x) = logb(x), where f(x) is the output value (usually y) and x is the input value (usually the variable). Logarithmic functions have unique properties that make them useful in solving equations and analyzing exponential growth or decay. For example, logarithmic functions can transform exponential growth into linear growth, allowing us to better understand and analyze the underlying patterns.
- One important property of logarithms is the change of base formula, which allows us to convert logarithms with one base to logarithms with another base.
- Logarithms also obey certain rules, such as the product rule and the power rule, which simplify calculations and manipulations involving logarithmic expressions.
- Logarithmic functions have a specific shape on a graph, with an asymptote at the y-axis and an increasing or decreasing behavior depending on the base.
- Logarithms can be used to solve various types of equations, such as exponential equations, logarithmic equations, and equations involving both exponential and logarithmic terms.
In conclusion, understanding logarithms and logarithmic functions is essential for solving equations involving exponential growth or decay and for analyzing patterns in various fields. They provide a powerful mathematical tool that simplifies calculations, converts exponential growth into linear growth, and helps us gain insights into the underlying processes.
Key Properties of Logarithms
Logarithms are mathematical functions that have several key properties that make them useful in a variety of applications. Understanding these properties can help simplify calculations and solve complex equations.
Property 1: The logarithm of a product is equal to the sum of the logarithms of the individual factors.
One of the fundamental properties of logarithms is that the logarithm of a product is equal to the sum of the logarithms of the individual factors. Mathematically, this can be expressed as:
logb(xy) = logb(x) + logb(y)
This property allows for easy calculation of logarithms when dealing with multiplication or division. Instead of calculating the logarithm of the entire product, you can simply add the logarithms of the individual factors.
Property 2: The logarithm of a power is equal to the product of the logarithm and the exponent.
Another important property of logarithms is that the logarithm of a power is equal to the product of the logarithm and the exponent. Mathematically, this can be expressed as:
logb(xn) = n * logb(x)
This property can be used to simplify calculations involving powers. Instead of calculating the logarithm of a power, you can simply multiply the logarithm of the base by the exponent.
Property 3: The logarithm of a quotient is equal to the difference of the logarithms of the numerator and the denominator.
The last property we will discuss is the logarithm of a quotient, which is equal to the difference of the logarithms of the numerator and the denominator. Mathematically, this can be expressed as:
logb(x/y) = logb(x) – logb(y)
This property can simplify calculations involving division. Instead of calculating the logarithm of the entire quotient, you can simply subtract the logarithms of the numerator and denominator.
These key properties of logarithms are essential tools for solving equations, simplifying calculations, and understanding the behavior of logarithmic functions. By applying these properties, mathematicians and scientists can make complex calculations more manageable and gain insights into various phenomena.
How to Solve Logarithmic Equations

Logarithmic equations can often be tricky to solve because they involve inverse functions and require a different approach compared to other types of equations. However, by following a few steps, you can successfully solve logarithmic equations.
Step 1: Identify the type of logarithmic equation
Logarithmic equations can be of two types: equations with a single logarithm or equations with multiple logarithms. It is important to identify the type of equation you are dealing with before proceeding to solve it.
Step 2: Simplify the equation
If your equation contains multiple logarithms, you can simplify it by using the properties of logarithms. Use the logarithmic identities such as the product rule, quotient rule, or power rule to combine multiple logarithms into a single logarithm.
Step 3: Apply the properties of logarithms
Once you have simplified the equation, apply the properties of logarithms to isolate the variable. For example, if you have a logarithm with a base of 10 and a constant term, you can use the property that log base 10 of a number equals x can be rewritten as 10 to the power of x equals the number.
Step 4: Solve for the variable
With the logarithm isolated, you can now solve for the variable. Depending on the equation, you may need to use algebraic techniques such as factoring, completing the square, or using the quadratic formula to solve for the variable.
Step 5: Check your solution
After finding the solution for the variable, it is important to check that it satisfies the original logarithmic equation. Substitute the solution back into the equation and verify that both sides are equal.
By following these steps and practicing with various logarithmic equations, you can become proficient in solving logarithmic equations and apply them to real-world problems.
Common mistakes when working with logarithms
Working with logarithms can be tricky, and it’s easy to make mistakes if you’re not careful. Here are some common mistakes to watch out for:
- Forgetting the rules of logarithms: Logarithms have their own set of rules that must be followed when manipulating and solving equations. Forgetting or misunderstanding these rules can lead to errors in your calculations.
- Mistaking the base of the logarithm: It’s important to correctly identify the base of the logarithm when solving equations. Using the wrong base can completely change the result.
- Confusing the notation: Logarithms have their own notation, with different symbols and conventions. Mixing up these notations or misinterpreting them can lead to errors.
- Canceling logarithms incorrectly: Sometimes, you may need to cancel logarithms in an equation. However, canceling them incorrectly can lead to incorrect results. It’s important to carefully apply the rules of logarithms when canceling them.
In order to avoid these mistakes, it’s important to have a solid understanding of logarithmic rules and properties. Practice working with logarithms, double-check your calculations, and make sure to pay attention to the details. By being mindful of these common mistakes, you can improve your accuracy when working with logarithms and logarithmic functions.
Applications of logarithms in real life
Logarithms, a mathematical concept introduced by John Napier in the 17th century, have found numerous applications in various fields of science, engineering, and finance. Here are some examples of how logarithms are used in real-life:
1. Earthquake intensity measurement:
The Richter scale, which measures the intensity of earthquakes, uses logarithms. Each increase of one on the Richter scale corresponds to a tenfold increase in the magnitude of the earthquake. For example, an earthquake with a magnitude of 4 is ten times stronger than an earthquake with a magnitude of 3. This logarithmic scale allows scientists to accurately quantify and compare the strength of different earthquakes.
2. pH scale for acid and base:
The pH scale, which measures the acidity or alkalinity of a substance, uses logarithms. The pH scale is logarithmic, with each unit representing a tenfold difference in acidity or alkalinity. For example, a substance with a pH of 3 is ten times more acidic than a substance with a pH of 4. This logarithmic scale allows chemists to measure and compare the acidity or alkalinity of different substances.
3. Exponential growth and decay:
Logarithms are used to model various natural phenomena that exhibit exponential growth or decay. For example, in population growth studies, logarithms help analyze and predict the growth rate of a population over time. Logarithmic functions are also used in radioactive decay calculations, financial investments, and the spread of diseases.
4. Sound and music:
The decibel scale, which measures the intensity of sound, uses logarithms. The decibel scale allows us to compare the loudness of different sounds and express them in a more manageable range. For example, a sound that is 10 decibels louder than another sound is actually ten times more intense. Logarithms are also used in music theory to calculate the frequency ratios between different musical notes.
In conclusion, logarithms have a wide range of applications in various fields, enabling scientists, engineers, and mathematicians to quantify and analyze complex phenomena. Whether it’s measuring earthquake intensity, analyzing population growth, or understanding the properties of sound, logarithms play a vital role in real-life scenarios.
Logarithmic functions in exponential growth and decay
In mathematics, logarithmic functions play a crucial role in understanding exponential growth and decay. These functions describe the relationship between the exponent and the base of an exponential equation, allowing us to solve for unknown variables and make predictions about changing quantities over time.
When dealing with exponential growth, logarithmic functions help us determine the rate at which a quantity increases. For example, if we have an exponential equation that represents population growth, the logarithmic function can tell us how quickly the population is growing at any given time. This information is essential in fields such as biology and economics, where understanding growth rates is crucial for making informed decisions.
Similarly, logarithmic functions are also used to understand exponential decay, which describes the process of a quantity decreasing over time. For instance, if we are dealing with radioactive decay, the logarithmic function can help us determine the rate at which the substance is decaying and how much is left after a certain period.
In both exponential growth and decay scenarios, logarithmic functions allow us to model and understand the underlying processes, enabling us to make predictions and analyze data effectively. They provide a mathematical tool for quantifying exponential change and exploring various real-world phenomena in fields such as finance, physics, and environmental science.
Graphing logarithmic functions
Graphing logarithmic functions is an important topic in mathematics, particularly in the study of algebra and calculus. Logarithmic functions involve the use of logarithms, which are mathematical operations that allow us to solve exponential equations. Understanding how to graph logarithmic functions is crucial in various applications, such as analyzing population growth, modeling natural phenomena, and solving complex equations.
To graph a logarithmic function, we first need to understand its general form. A logarithmic function is typically written as y = logb(x), where x is the input variable and b is the base of the logarithm. The graph of this function will have specific characteristics depending on the value of b and any additional transformations or shifts applied to the function.
One key feature of logarithmic functions is the presence of an asymptote, which is a line that the graph approaches but never touches. The position of the asymptote depends on the base of the logarithm. For example, if the base is greater than 1, the asymptote will be a horizontal line above the x-axis. On the other hand, if the base is between 0 and 1, the asymptote will be a horizontal line below the x-axis.
Additionally, the direction and shape of the graph will vary depending on the value of b. If b is greater than 1, the graph will be increasing as x moves to the right. Conversely, if b is between 0 and 1, the graph will be decreasing as x moves to the right. The steepness of the graph will also be affected by the value of b, with larger values resulting in steeper curves and smaller values resulting in flatter curves.
By understanding these key features and characteristics of logarithmic functions, we can accurately graph them and analyze their behavior in various contexts. Graphing logarithmic functions is an essential skill for students and professionals in the fields of mathematics, science, and engineering, as it allows us to solve complex equations and model real-world phenomena.