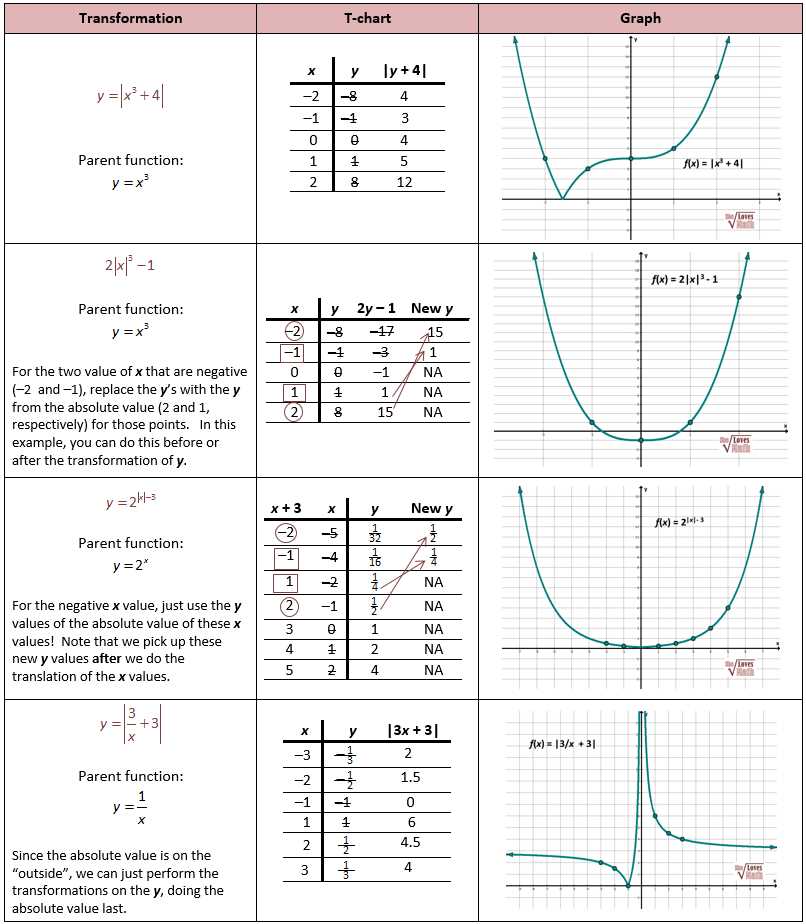
Understanding the concept of transformations is essential when working with mathematical functions, especially exponential functions. In this article, we will explore 7 different skills practice questions that focus on transformations of exponential functions.
Exponential functions are functions of the form f(x) = a^x, where a is a constant and x is the independent variable. These functions are widely used to model growth and decay in various scientific and economic contexts. Transformations of exponential functions involve modifying key elements of the function to create different graphs and better represent real-world scenarios.
In the skills practice questions, you will encounter different transformations such as vertical and horizontal shifts, stretching and compressing, and reflection. Each question will require you to analyze the given exponential function and apply the appropriate transformation to obtain the desired result. By practicing these skills, you will gain a deeper understanding of how transformations affect the shape and behavior of exponential functions.
It is crucial to have a strong grasp of transformations when studying exponential functions, as they allow you to accurately represent real-life data and make predictions based on mathematical models. By mastering these skills, you will enhance your ability to interpret and manipulate exponential functions, opening up new possibilities for analyzing various phenomena.
Skills Practice: Transformations of Exponential Functions Answers
In this skills practice, students are given the opportunity to apply their knowledge of exponential functions and their transformations. By working through a series of exercises and problems, students can solidify their understanding of how changes in certain parameters can affect the shape and behavior of exponential functions.
One possible solution for the exercise on transforming exponential functions could be as follows:
- To transform the function (y = 2^x) three units to the right, we can rewrite the function as (y = 2^{(x-3)}).
- To transform the function (y = 2^x) two units up, we can rewrite the function as (y = 2^x + 2).
- To transform the function (y = 2^x) vertically stretched by a factor of 3, we can rewrite the function as (y = 3 cdot 2^x).
- To transform the function (y = 2^x) horizontally compressed by a factor of 2, we can rewrite the function as (y = 2^{(x/2)}).
- To transform the function (y = 2^x) reflected over the x-axis, we can rewrite the function as (y = -2^x).
These are just a few examples of how exponential functions can be transformed using different operations. By practicing these exercises, students can develop a strong understanding of how changes in the equation can impact the shape and behavior of exponential functions.
Understanding Exponential Functions
An exponential function is a mathematical expression that shows the relationship between an independent variable and its corresponding dependent variable. These functions have the form y = a * b^x, where a and b are constants, and x is the independent variable. The base b is typically greater than 1 and determines the rate at which the dependent variable grows or decays.
Exponential functions are characterized by their rapid growth or decay. As the independent variable increases, the dependent variable grows exponentially, meaning it increases at an accelerating rate. Conversely, as the independent variable decreases, the dependent variable decays exponentially, meaning it decreases at a decelerating rate.
Exponential functions can be used to model a wide range of real-world phenomena, such as population growth, radioactive decay, compound interest, and the spread of infectious diseases. These functions are particularly useful in situations where the rate of change is proportional to the current value of the variable.
To better understand exponential functions, it is important to study their transformations. These transformations include vertical translations, horizontal translations, reflections over the x-axis, and vertical stretches or compressions. By manipulating these transformations, we can shift and scale the graph of an exponential function to fit specific situations or data.
By studying exponential functions and their transformations, we can gain insights into various phenomena and make predictions about their future behavior. Understanding the properties and behaviors of exponential functions is crucial in fields such as finance, biology, physics, and economics, where exponential growth or decay is commonly observed.
Identifying the Basic Form of an Exponential Function
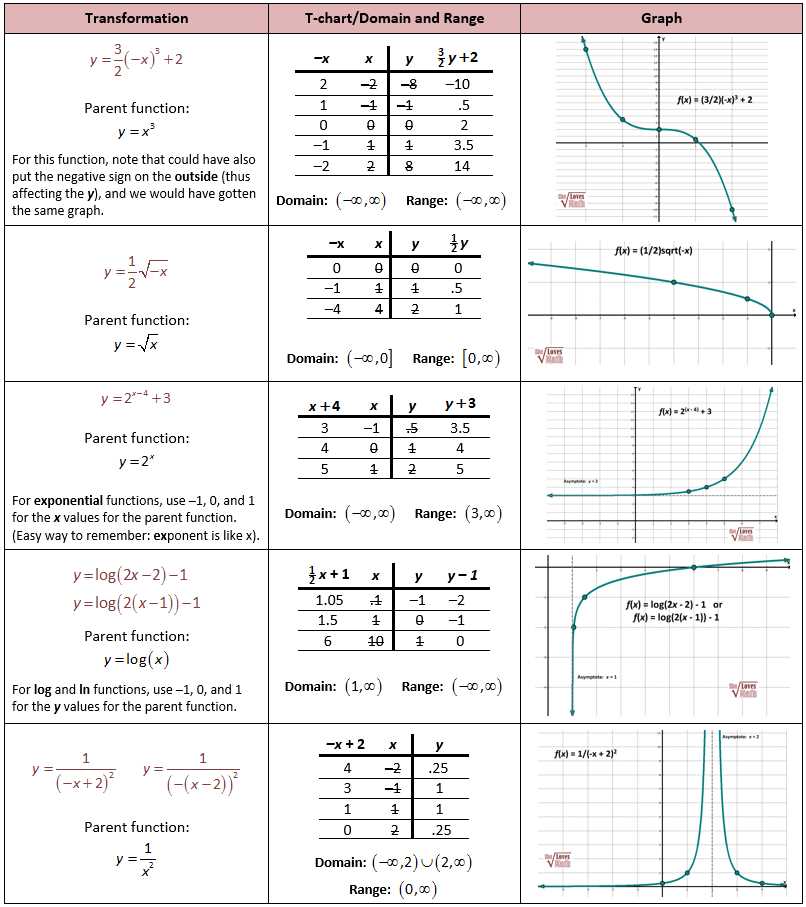
An exponential function is a mathematical function where the independent variable is in the exponent. It can be written in the form y = ab^x, where a and b are constants.
To identify the basic form of an exponential function, we look for specific patterns in the equation. The base, b, is the constant multiplier or factor that is raised to the power of x. It determines the shape and direction of the graph. The constant a is the initial value or the value of y when x is equal to zero.
For example, in the equation y = 2^x, the base is 2. This means that the function is multiplying by 2 each time x increases by 1. The graph of this function will show exponential growth. The initial value is not specified in this equation, but it will be the value of y when x is equal to zero.
In another example, if we have the equation y = 3(0.5)^x, the base is 0.5. This means that the function is multiplying by 0.5 each time x increases by 1. The graph of this function will show exponential decay. The constant a in this equation is 3, which is the y-coordinate when x is equal to zero.
By identifying the basic form of an exponential function, we can understand the behavior and characteristics of the function and use it to make predictions and solve problems in various fields, such as finance, population growth, and scientific modeling.
Graphing Exponential Functions
Graphing exponential functions is an important skill in mathematics. Exponential functions are characterized by the constant growth or decay rate, which is represented by the base of the function. The general form of an exponential function is given by:
f(x) = a * b^x
Where a is the initial value, b is the growth or decay factor, and x is the variable. To graph an exponential function, we need to choose a set of values for x, calculate the corresponding values of y using the given function, and plot the points on a coordinate plane.
Example:
Let’s graph the exponential function f(x) = 2^x. We can choose a range of values for x, calculate the corresponding values of y, and plot the points:
| x | y |
|---|---|
| -2 | 0.25 |
| -1 | 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
Plotting these points on a graph, we can see that the exponential function f(x) = 2^x exhibits exponential growth, as the values of y increase rapidly as x increases.
Graphing exponential functions helps us visualize and understand how these functions behave. It allows us to identify important characteristics such as the initial value, growth or decay rate, and any transformations applied to the function. By analyzing the graph, we can make predictions and solve problems related to exponential functions.
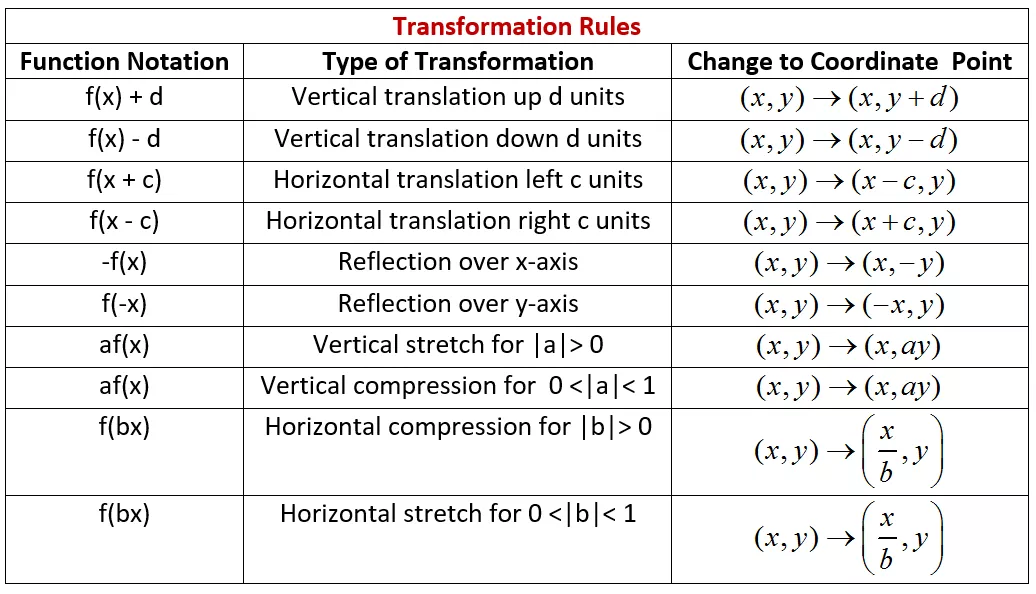
Applying Transformations to Exponential Functions
Transformations play a crucial role in understanding and analyzing exponential functions. By applying various transformations, we can manipulate the shape, position, and characteristics of an exponential function graph. These transformations allow us to explore how changes in the parameters of an exponential function affect its behavior.
When we talk about transformations of exponential functions, we usually refer to changes in the base, the coefficient, and the exponent. Each of these transformations has a distinct effect on the graph of an exponential function.
- Changing the base: Changing the base of an exponential function results in a vertical stretch or compression of the graph. An exponential function with a base greater than 1 will display a faster growth or decay, while a base between 0 and 1 will exhibit a slower growth or decay.
- Changing the coefficient: Changing the coefficient before the exponential term affects the vertical position of the graph. It acts as a vertical translation, shifting the entire graph up or down.
- Changing the exponent: Changing the exponent of an exponential function modifies the steepness of the curve. Increasing the exponent leads to a steeper curve, while decreasing the exponent results in a flatter curve.
By combining these transformations, we can create complex exponential functions and explore their behaviors. It is important to understand these transformations in order to analyze real-world data, make predictions, and solve various problems involving exponential functions.
| Transformation | Effect on the Function |
|---|---|
| Change in base | Vertical stretch or compression |
| Change in coefficient | Vertical translation |
| Change in exponent | Steepness of the curve |
By mastering the art of applying transformations to exponential functions, we can gain insights into the behavior of various phenomena, such as population growth, radioactive decay, and compound interest. These transformations allow us to model and understand the world around us through the lens of exponential functions.
Finding the Equation for a Transformed Exponential Function
Transforming exponential functions involves making changes to the original function by performing various operations such as shifting, stretching, and reflecting. These transformations can alter the appearance and behavior of the function, allowing us to model real-world situations more accurately.
To find the equation for a transformed exponential function, we need to understand the effects of each transformation. The general form of an exponential function is y = a * b^x + c, where “a” represents the initial value, “b” is the base, “x” is the input variable, and “c” is a constant term.
Shifting the function horizontally involves adding or subtracting a value, “h”, inside the exponent. If “h” is positive, the function will shift to the left, and if “h” is negative, it will shift to the right. The equation for a horizontal shift is y = a * b^(x – h) + c.
Stretching or shrinking the function vertically is done by multiplying the entire function by a vertical scaling factor, “d”. If “d” is greater than 1, the function will stretch vertically, and if “d” is between 0 and 1, it will shrink. The equation for a vertical stretch or shrink is y = d * a * b^x + c.
Reflecting the function across the x-axis involves adding a negative sign to the base, “-b”. This reflection will change the shape of the curve. The equation for a reflection across the x-axis is y = a * (-b)^x + c.
By combining these transformations and applying the appropriate operations, we can find the equation for a transformed exponential function that accurately represents the given situation. Understanding the effects of each transformation helps us interpret and analyze the behavior of the function in relation to the original function.
Solving Problems with Exponential Functions
Exponential functions are extremely useful in solving various problems, especially those involving growth or decay. These functions represent a relationship where the value of a quantity changes at a constant rate over a certain time period. Solving problems with exponential functions requires understanding the properties of these functions and how they behave.
One common type of problem involves finding the value of a quantity after a certain amount of time has passed. In these cases, we can use the formula for exponential growth or decay to calculate the final value. This formula is typically written as:
P(t) = P0 * e^(kt)
Where P(t) is the final value, P0 is the initial value, k is the growth or decay rate, and t is the time period. By plugging in the known values, we can solve for the unknown value.
Another type of problem involves finding the time it takes for a quantity to reach a certain value. In these cases, we need to rearrange the formula and solve for t instead. This can be done by taking the natural logarithm of both sides and isolating t.
Understanding exponential functions also helps in analyzing and interpreting data. For example, when studying population growth, we can use exponential functions to project future population size based on growth rates. Similarly, in finance, we can use exponential functions to model compound interest and calculate future investment returns.
Overall, solving problems with exponential functions involves applying the properties and formulas of these functions to specific situations. By understanding how exponential functions behave, we can accurately analyze and predict various phenomena, from population growth to financial investments.
Applying Exponential Functions in Real-Life Scenarios
In mathematics, exponential functions play a crucial role in modeling various real-life scenarios. These functions are characterized by the equation f(x) = a^x, where “a” is a constant and “x” represents the input. Exponential functions exhibit rapid growth or decay, making them ideal for describing phenomena such as population growth, compound interest, and radioactive decay.
One of the most common applications of exponential functions is in the field of finance. For example, consider compound interest. The formula for compound interest is given by P(t) = P₀(1 + r/n)^(nt), where P(t) represents the amount of money at time “t,” P₀ is the initial principal, r is the annual interest rate, and n is the number of times the interest is compounded per year. This formula can be expressed as an exponential function, allowing individuals to calculate the growth of their investments over time.
Another real-life scenario where exponential functions are applied is in population growth. The growth of populations, whether it be the human population or the population of organisms, often follows an exponential growth pattern. Exponential functions can help model and predict population growth, enabling policy-makers and scientists to anticipate the needs and challenges associated with increasing populations.
Furthermore, exponential functions are also used to describe radioactive decay. Radioactive decay is a natural process where unstable atoms break down over time, releasing radiation. The rate at which this decay occurs follows an exponential function. Scientists and researchers use exponential functions to study the decay process, determine half-lives, and analyze the potential risks and benefits of radioactive materials.
In summary, exponential functions are versatile mathematical tools that have a wide range of applications in real-life scenarios. Whether it’s in finance, population growth, or radioactive decay, exponential functions provide valuable insights and predictions. Understanding the principles behind exponential functions allows us to make informed decisions and solve complex problems in various fields of study.