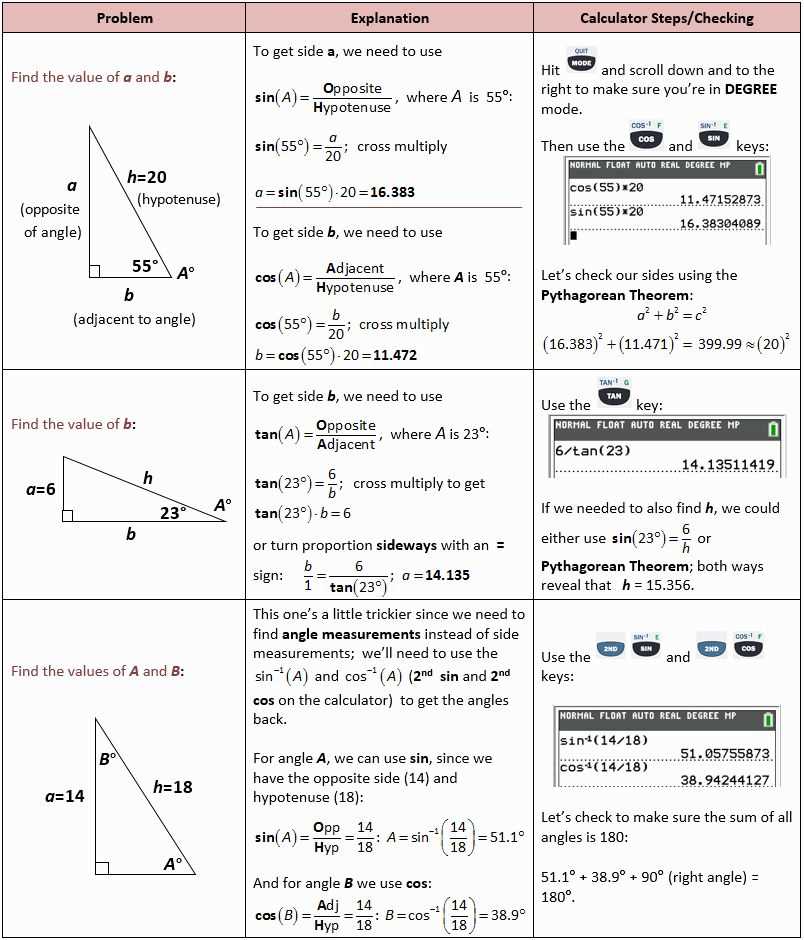
The process of solving right triangles involves finding the missing sides and angles of a triangle when one or more of these values are not given. By using the properties of right triangles, such as the Pythagorean theorem and trigonometric ratios, we can determine the unknown values.
In this 9 6 solving right triangles answer key, we will explore a variety of problem-solving techniques to find missing sides and angles in right triangles. By applying the principles of trigonometry, we can use sine, cosine, and tangent ratios to determine the values of the angles and sides.
One of the most important concepts in solving right triangles is the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem allows us to find missing side lengths by setting up an equation and solving for the unknown value.
By utilizing the concepts of trigonometry and the Pythagorean theorem, this 9 6 solving right triangles answer key provides step-by-step solutions to a variety of problems. Whether you are a student learning the basics of right triangles or a professional needing to solve real-world problems, this answer key will guide you through the process of finding missing values in right triangles.
Understanding Right Triangles
Right triangles are an important concept in geometry and trigonometry. They are defined as triangles that have one angle measuring exactly 90 degrees, which is called the right angle. Understanding right triangles is key to solving various mathematical and real-world problems.
In a right triangle, the side opposite the right angle is called the hypotenuse. The other two sides are known as the legs. The relationships between the sides of a right triangle are defined by the Pythagorean theorem, which states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
One of the fundamental applications of right triangles is in trigonometry. Trigonometric functions such as sine, cosine, and tangent are defined based on the ratios of the lengths of the sides of a right triangle. These functions are widely used in fields such as engineering, physics, and navigation to calculate distances, angles, and heights.
Knowing how to solve right triangles is essential in trigonometry. To solve a right triangle, you need to find the lengths of all the sides and the measures of all the angles. This can be done using trigonometric functions, the Pythagorean theorem, and other geometric principles. Solving right triangles allows us to find missing information and accurately determine the properties of a triangle.
In conclusion, understanding right triangles is crucial in various mathematical and practical applications. They provide the foundation for trigonometry and enable us to solve complex problems involving distances, angles, and heights. Mastering the concepts and techniques of right triangles is an essential skill for anyone studying geometry or trigonometry.
Definition and Properties
When dealing with right triangles, it is important to understand their definition and properties. A right triangle is a type of triangle that has one angle measuring 90 degrees, which is called a right angle. The other two angles in a right triangle are acute angles, meaning they are less than 90 degrees. The side opposite the right angle is called the hypotenuse, while the other two sides are known as the legs.
One of the most important properties of right triangles is the Pythagorean theorem, which states that the square of the hypotenuse is equal to the sum of the squares of the legs. This theorem can be expressed using the formula a^2 + b^2 = c^2, where a and b are the lengths of the legs, and c is the length of the hypotenuse. This theorem allows us to solve for the lengths of the sides of a right triangle when we know the lengths of the other two sides.
Another property of right triangles is that the lengths of the sides are related to the angles of the triangle. The sine, cosine, and tangent functions can be used to find the ratios between the lengths of the sides and the measures of the angles. For example, the sine of an acute angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
In summary, right triangles have a unique set of properties that make them different from other types of triangles. Understanding these properties, such as the Pythagorean theorem and the relationships between the lengths of the sides and the angles, is essential when solving problems involving right triangles.
Special Right Triangles
In geometry, special right triangles are triangles that have simple and easily recognizable ratios between their side lengths. These ratios can be used to find missing side lengths or angles in a right triangle without the need for complex calculations.
There are two main types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle. In a 45-45-90 triangle, the two legs are congruent and the hypotenuse is equal to the length of one of the legs multiplied by the square root of 2. This triangle is useful in many applications, such as when constructing perpendicular lines or finding diagonal lengths in squares.
In a 30-60-90 triangle, the ratio of the lengths of the sides is 1:√3:2. The side opposite the 30 degree angle is half the length of the hypotenuse, and the side opposite the 60 degree angle is equal to the length of the hypotenuse multiplied by the square root of 3. This type of triangle is often used in trigonometry and geometry to find missing side lengths or angles.
Understanding the properties of these special right triangles can greatly simplify problem-solving in geometry. By recognizing the ratios and applying them appropriately, students can quickly find solutions without the need for lengthy calculations. This knowledge is essential for success in math and can be applied to a wide range of real-world problems.
Solving Right Triangles
When it comes to solving right triangles, there are several key steps and formulas that can be used to find missing sides and angles. Right triangles are triangles that have one angle measuring 90 degrees, also known as a right angle. The other two angles in a right triangle are acute angles, meaning they are less than 90 degrees.
In order to solve a right triangle, you need at least one known side length or angle measure. With this information, you can use the Pythagorean theorem, trigonometric ratios, and basic geometry principles to find the missing sides and angles. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
To begin solving a right triangle, you can use the Pythagorean theorem to find the length of the missing side if you know the lengths of the other two sides. This is particularly useful when dealing with a right triangle where the angle measures are not provided. Once you have the lengths of all three sides, you can then use trigonometric ratios such as sine, cosine, and tangent to find the missing angle measures.
When solving right triangles, it is important to remember that there can be multiple solutions. This is because trigonometric ratios are periodic functions, meaning they repeat values after a certain interval. As a result, there may be more than one angle that satisfies the given conditions of the triangle. It is important to consider the context and restrictions of the problem to determine the appropriate solution.
In conclusion, solving right triangles involves using the Pythagorean theorem and trigonometric ratios to find missing sides and angles. By applying these formulas and principles, you can determine the complete set of measurements for a given right triangle. It is important to consider multiple solutions and understand the context of the problem to ensure accurate calculations and interpretations.
Finding Missing Sides
When working with right triangles, it is often necessary to find the lengths of missing sides. This can be done using the Pythagorean theorem, trigonometric ratios, or special right triangles.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Using this theorem, we can find missing sides by rearranging the equation and solving for the unknown side.
- Example: Given a right triangle with one leg measuring 3 units and the hypotenuse measuring 5 units, we can find the length of the other leg using the Pythagorean theorem. Rearranging the equation: (a^2 + b^2 = c^2), where (a) and (b) are the legs and (c) is the hypotenuse, we have (3^2 + b^2 = 5^2). Solving for (b), we get (b^2 = 5^2 – 3^2), which simplifies to (b^2 = 25 – 9). Taking the square root of both sides, we find that (b = sqrt{16}), so (b = 4) units.
Trigonometric ratios, such as sine, cosine, and tangent, can also be used to find missing sides in right triangles. These ratios relate the lengths of the sides of a right triangle to its angles.
- Example: Given a right triangle with an angle of 30 degrees and a hypotenuse of 10 units, we can find the length of the opposite side using the sine ratio. The sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. In this case, the sine of 30 degrees is ( frac{opposite}{hypotenuse} ), so we have ( sin 30^{circ} = frac{opposite}{10} ). Rearranging the equation, we find that the length of the opposite side is ( sin 30^{circ} times 10 ), which simplifies to ( frac{1}{2} times 10 = 5 ) units.
Special right triangles, such as the 45-45-90 and 30-60-90 triangles, have ratios of side lengths that can be used to find missing sides. These ratios are constant and can be easily memorized.
- Example: In a 45-45-90 triangle, the ratio of the length of the legs to the length of the hypotenuse is 1:1:(sqrt{2}). So, if we know the length of one leg, we can easily find the length of the other leg or the hypotenuse by multiplying by the appropriate ratio.
In summary, there are several methods for finding missing sides in right triangles, including the Pythagorean theorem, trigonometric ratios, and special right triangles. These methods can be used based on the given information and the specific problem at hand.
Finding Missing Angles
When working with right triangles, it is often necessary to find missing angles in order to solve a problem or fully understand the triangle’s properties.
One common method for finding missing angles in right triangles is to use trigonometric ratios such as sine, cosine, and tangent. These ratios relate the angles of a right triangle to the lengths of its sides. By knowing the lengths of two sides of a right triangle, we can use these trigonometric ratios to find the size of the angles.
For example, if we know the length of the opposite side and the length of the hypotenuse of a right triangle, we can use the sine ratio to find the size of the angle opposite the known side. Similarly, if we know the lengths of the adjacent side and the hypotenuse, we can use the cosine ratio to find the angle adjacent to the known side.
Another method for finding missing angles in right triangles is to use the Pythagorean theorem. This theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. By rearranging this equation and solving for the missing angle, we can find its size.
It’s important to note that in some cases, the missing angle may not be easily solvable using these methods. In such cases, advanced mathematical techniques may be required, or the problem may need to be approached from a different angle.
Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a right triangle to the ratios of its sides. These functions include sine, cosine, and tangent, as well as their reciprocals: cosecant, secant, and cotangent. Trigonometry is an essential branch of mathematics that has applications in various fields such as physics, engineering, and architecture.
The sine function (sin) represents the ratio of the length of the side opposite the angle to the hypotenuse. It is usually denoted as sin(θ), where θ is the angle. The cosine function (cos) represents the ratio of the length of the adjacent side to the hypotenuse. It is denoted as cos(θ). The tangent function (tan) represents the ratio of the length of the opposite side to the adjacent side. It is denoted as tan(θ).
Some key properties of trigonometric functions include:
- The sine function is an odd function, meaning that sin(-θ) = -sin(θ).
- The cosine function is an even function, meaning that cos(-θ) = cos(θ).
- The tangent function has period π, which means that tan(θ + π) = tan(θ).
- The reciprocal functions, cosecant (csc), secant (sec), and cotangent (cot), are defined as the reciprocals of sin, cos, and tan, respectively.
Trigonometric functions are widely used in solving right triangles, where the lengths of some of the sides are known and the remaining angles and sides need to be determined. They are also used in analyzing periodic phenomena such as waves and oscillations. Understanding trigonometric functions is crucial for those studying mathematics, physics, and engineering.
Sine, Cosine, and Tangent
The sine, cosine, and tangent functions are trigonometric functions that are used to relate the angles and sides of a right triangle. These functions are fundamental in trigonometry and have applications in various fields, including physics, engineering, and geometry.
The sine function (abbreviated as sin) relates the ratio of the length of the side opposite an angle to the length of the hypotenuse of a right triangle. It is defined as the y-coordinate of a point on the unit circle corresponding to a specific angle. The sine function has a range from -1 to 1, with the maximum value of 1 occurring at 90 degrees and the minimum value of -1 occurring at 270 degrees.
The cosine function (abbreviated as cos) relates the ratio of the length of the side adjacent to an angle to the length of the hypotenuse of a right triangle. It is defined as the x-coordinate of a point on the unit circle corresponding to a specific angle. The cosine function also has a range from -1 to 1, with the maximum value of 1 occurring at 0 degrees and the minimum value of -1 occurring at 180 degrees.
The tangent function (abbreviated as tan) is the ratio of the length of the side opposite an angle to the length of the side adjacent to that angle in a right triangle. It can also be defined as the sine divided by the cosine of an angle. The tangent function is useful for determining angles and distances in real-world scenarios, such as finding the angle of elevation or depression.
In summary, the sine, cosine, and tangent functions are essential tools for solving right triangles and understanding the relationships between angles and sides. They provide a mathematical framework for analyzing and solving various problems in trigonometry.