Understanding and accurately calculating measures of central tendency, dispersion, and variability is essential in statistics. One way to ensure mastery of these concepts is by practicing with real-world examples. In this article, we will provide an answer key for a practice exercise on mean, median, mode, and range using data from AFDA (Association of Film and Drama Academics).
The AFDA Mean Median Mode Range Practice Exercise consists of a series of questions based on data collected from film and drama academic programs. The questions require students to apply their knowledge of these statistical measures to analyze and interpret the data. By working through these exercises and referring to the answer key provided, students can assess their understanding and identify areas that need improvement.
The answer key will include step-by-step explanations and calculations for each question, allowing students to follow along and understand the process. Additionally, the answer key will provide tips and strategies to help students approach similar problems in the future. Whether you are a student preparing for a statistics exam or someone interested in improving their data analysis skills, this answer key will serve as a valuable resource.
Understanding the mean

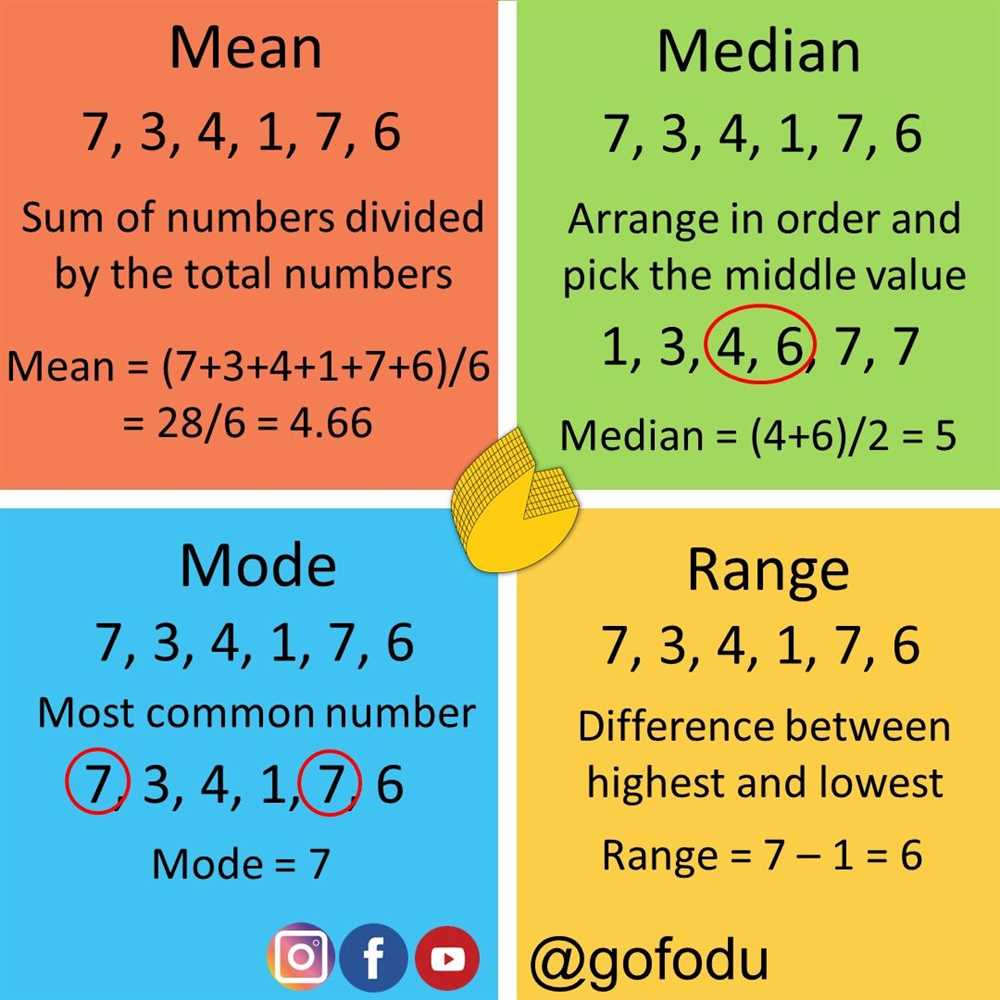
The mean is a measure of central tendency that helps us understand the average value of a set of numbers. It is calculated by adding up all the values in the set and dividing by the total number of values. For example, if we have a set of numbers {2, 4, 6, 8, 10}, the mean would be (2 + 4 + 6 + 8 + 10) / 5 = 6.
The mean is useful because it gives us a single number that represents the typical value in a set. It can help us compare sets of data and understand their overall behavior. For example, let’s say we have the heights of five students: 150 cm, 160 cm, 170 cm, 180 cm, and 190 cm. The mean height would be (150 + 160 + 170 + 180 + 190) / 5 = 170 cm. This tells us that the average height of the students is 170 cm.
The mean can also be affected by extreme values in a data set. If we have a set of numbers {2, 4, 6, 8, 100}, the mean would be (2 + 4 + 6 + 8 + 100) / 5 = 24. This means that even though the majority of the numbers are small, the presence of the large value 100 significantly affects the mean. In such cases, it can be useful to consider other measures of central tendency, such as the median or mode, to get a better understanding of the data.
In summary, the mean is a valuable tool for understanding the average value in a set of numbers. It provides a single number that represents the typical value, but it can be influenced by extreme values. By considering other measures of central tendency, we can gain a more comprehensive understanding of the data.
Finding the Median in Afda Mean Median Mode Range Practice
When working with data sets, finding the median is an important step in understanding the central tendency of the data. In the context of afda mean median mode range practice, the median represents the middle value of a data set when it is ordered from least to greatest. It provides us with a measure of the central value that is resistant to outliers and extreme values.
To find the median, we first need to arrange the data set in ascending order. Once the data set is ordered, we can determine the middle value. If the data set has an odd number of values, the median is the middle value itself. For example, if we have the data set {2, 4, 6, 8, 10}, the median would be 6. However, if the data set has an even number of values, we need to find the average of the two middle values. For example, if we have the data set {1, 3, 5, 7}, the median would be the average of 3 and 5, which is 4.
In the context of afda mean median mode range practice, finding the median helps us understand the central value of a data set. It allows us to compare individual values to the median to determine if they are above or below the central tendency. Additionally, finding the median helps us evaluate the spread of the data set and identify any potential outliers. By understanding the concept of median and how to calculate it, we can analyze and interpret data more effectively.
Overall, finding the median in afda mean median mode range practice is an essential skill in analyzing and interpreting data. It provides us with a measure of the central value that is resistant to extreme values and allows us to evaluate the spread of the data set. By understanding the concept of median and how to calculate it, we can gain valuable insights from the data and make informed decisions based on the central tendency of the data set.
Identifying the mode in Afda mean median mode range practice

The mode is one of the measures used to describe the central tendency of a set of data in statistics. In the context of Afda mean median mode range practice, identifying the mode involves finding the most frequently occurring value or values in a given dataset. It provides valuable information about the data distribution and can be helpful in understanding the overall pattern of the data.
To determine the mode in Afda mean median mode range practice, one can observe the dataset and look for any repeating values. These repeating values are considered to be the mode. In some cases, there may be multiple modes if there are two or more values that occur with the same highest frequency.
For example, suppose we have the following dataset in an Afda mean median mode range practice exercise: 3, 4, 5, 4, 2, 5, 6. In this case, the mode would be 4 and 5, as they both occur twice, which is the highest frequency in the dataset. This means that in this particular dataset, both 4 and 5 are the most common values.
It is important to note that not all datasets have a mode. If no value is repeated in a dataset, then there is no mode. Additionally, a dataset can also have more than one mode if there is more than one value that occurs with the same highest frequency.
- In summary, the mode is the value or values that occur with the highest frequency in a dataset, making them the most common values.
- Identifying the mode in Afda mean median mode range practice involves looking for any repeating values.
- If no value is repeated, then there is no mode. If multiple values occur with the same highest frequency, there can be multiple modes.
Calculating the Range in Afda Mean Median Mode Range Practice

When practicing the Afda Mean Median Mode Range, it is important to understand how to calculate the range. The range is a measure of dispersion or spread in a set of data. It tells us how far apart the smallest and largest values are in a dataset. To calculate the range, we subtract the smallest value from the largest value.
For example, if we have a dataset of {3, 7, 9, 12, 15}, the smallest value is 3 and the largest value is 15. To find the range, we subtract 3 from 15, which gives us a range of 12. This means that the numbers in the dataset are spread out over a range of 12 units.
Calculating the range is a relatively simple process, but it provides valuable information about the spread of data. It can help us understand how much variability there is in a dataset and how close or far apart the individual values are from each other. By practicing the Afda Mean Median Mode Range and calculating the range, we can develop our mathematical skills and gain a better understanding of data analysis.
Example problem-solving in Afda mean median mode range practice

When practicing problems related to mean, median, mode, and range in Afda, it is important to have a clear understanding of each concept and how to calculate them. Let’s take a look at an example problem and go through the steps to find the solutions.
Example problem:
For a statistics class, a teacher asked her students to record their scores on a recent test. The scores obtained by the students were as follows: 85, 92, 78, 90, 88, 92, 85, 90, 80, 92. Calculate the mean, median, mode, and range of these scores.
Solution:
To find the mean, we need to sum up all the scores and divide it by the total number of scores. In this case, the sum of the scores is 852, and there are 10 students. Therefore, the mean is 852/10 = 85.2.
To find the median, we need to arrange the scores in ascending order. The sorted scores are 78, 80, 85, 85, 88, 90, 90, 92, 92, 92. Since there are 10 scores, the median is the average of the middle two values, which are 88 and 90. Therefore, the median is (88 + 90)/2 = 89.
To find the mode, we need to determine the score that appears most frequently. In this case, the score 92 appears three times, which is the highest frequency. Therefore, the mode is 92.
To find the range, we subtract the smallest score from the largest score. Here, the smallest score is 78 and the largest score is 92. Therefore, the range is 92 – 78 = 14.
In conclusion, the mean of the scores is 85.2, the median is 89, the mode is 92, and the range is 14. This example demonstrates how to apply the concepts of mean, median, mode, and range to solve a problem.