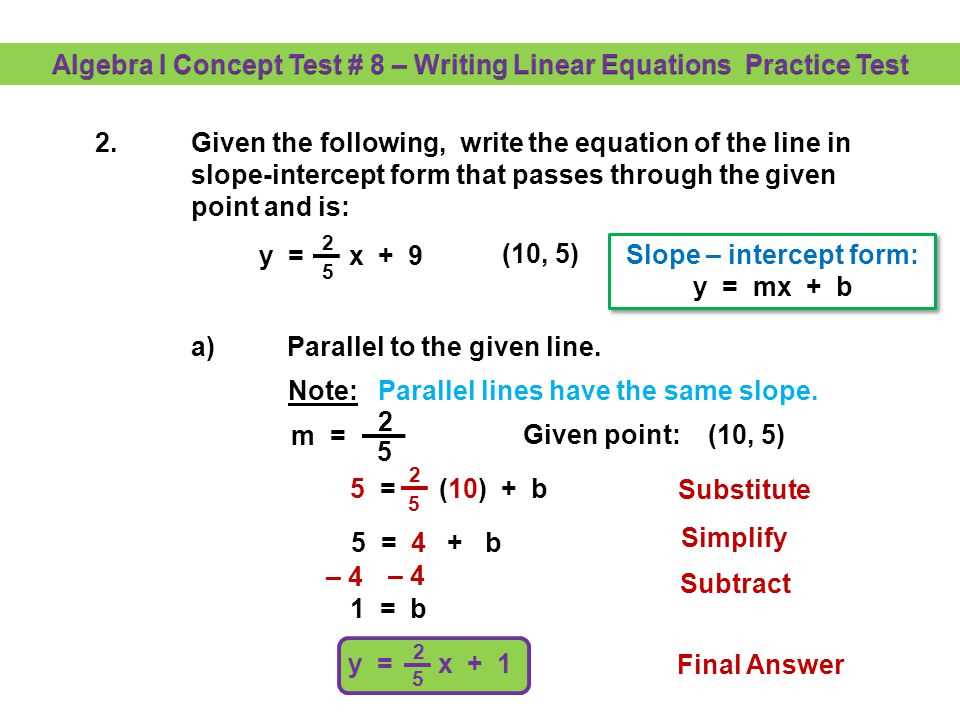
Algebra is a fundamental branch of mathematics that introduces students to the world of equations and unknown variables. It provides the necessary tools to solve real-life problems and lays the groundwork for more advanced mathematical concepts. Unit 2 of Algebra 1 delves deeper into the principles of algebra, covering topics such as linear equations, inequalities, and systems of equations.
The Algebra 1 Unit 2 test is designed to assess students’ understanding and mastery of these essential algebra concepts. This comprehensive examination evaluates their ability to solve linear equations, graph linear functions, interpret and manipulate inequalities, and solve systems of equations. It tests their mathematical reasoning, problem-solving skills, and ability to apply algebraic techniques in various contexts.
Preparing for the Algebra 1 Unit 2 test involves a combination of studying key concepts, practicing problem-solving techniques, and familiarizing oneself with the types of questions that may be asked. Students should review the properties of equality, learn to identify linear equations and their slopes, and understand the graphical representation of inequalities. They should also be proficient in solving systems of equations through different methods, such as substitution or elimination.
Understanding the Importance of Algebra 1 Unit 2 Test
Algebra 1 Unit 2 test is a crucial assessment that measures students’ understanding and proficiency in fundamental algebraic concepts. This test is designed to evaluate their ability to solve equations, analyze patterns, and apply mathematical reasoning to real-world problems. By assessing their knowledge and skills in unit 2, teachers can gauge students’ progress and provide targeted instruction to address any gaps in understanding.
The Algebra 1 Unit 2 test covers essential topics such as linear equations, systems of equations, inequalities, and functions. These concepts serve as building blocks for further studies in algebra and other branches of mathematics. Mastering unit 2 lays a strong foundation for students to confidently tackle more complex algebraic problems in higher grades and in various fields such as engineering, economics, and computer science.
The test helps in identifying individual strengths and weaknesses:
- By evaluating students’ performance in unit 2, teachers can identify areas where students excel and provide them with opportunities for enrichment and extension.
- Additionally, the test helps pinpoint specific areas where students struggle, allowing teachers to tailor their instruction and provide targeted support for individual student needs.
The test promotes critical thinking and problem-solving skills:
- Algebra 1 Unit 2 test requires students to think critically, analyze information, and apply mathematical reasoning to solve problems.
- By solving equations and working with various algebraic concepts, students develop problem-solving skills that can be applied in real-life situations.
The test prepares students for future assessments:
- Successfully completing the Algebra 1 Unit 2 test prepares students for more advanced algebraic assessments in higher grades.
- It helps them build the necessary skills and knowledge base to tackle future math courses and standardized tests.
In conclusion, the Algebra 1 Unit 2 test plays a vital role in assessing students’ understanding of fundamental algebraic concepts. It helps identify individual strengths and weaknesses, promotes critical thinking and problem-solving skills, and prepares students for future assessments. By recognizing the importance of this test, students and teachers can work together to ensure a strong foundation in algebra and pave the way for success in future mathematical pursuits.
What is Algebra 1 Unit 2 Test
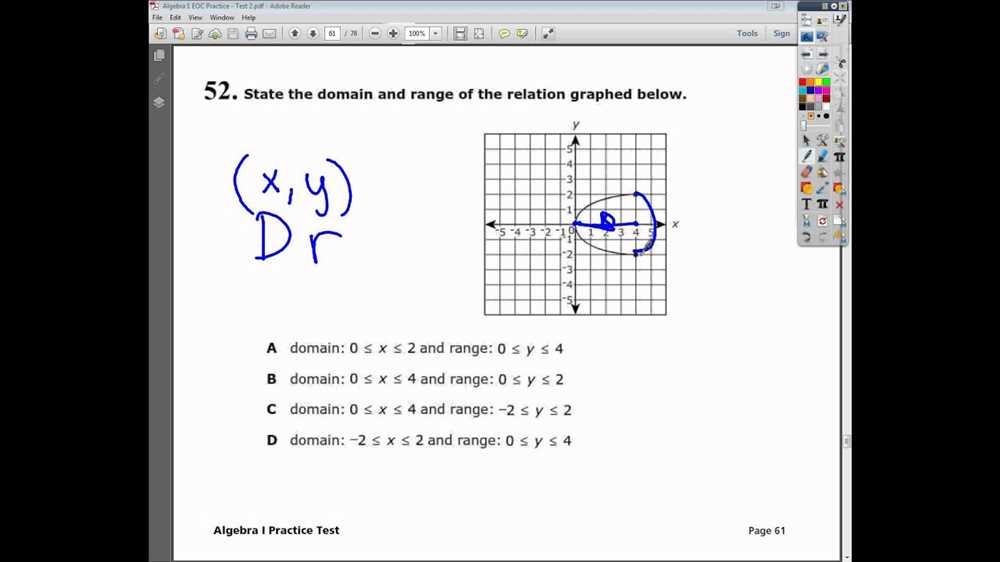
An Algebra 1 Unit 2 Test is an assessment designed to evaluate a student’s understanding and proficiency in the concepts and skills covered in Unit 2 of an Algebra 1 course. Unit 2 typically focuses on essential algebraic topics such as linear equations, inequalities, systems of equations, and their applications.
The test may include a variety of question types, including multiple-choice, short answer, and problem-solving questions. Students may be asked to solve equations and inequalities, graph linear functions, analyze real-world scenarios using algebraic models, and apply their knowledge to solve contextual problems.
Key concepts covered in Algebra 1 Unit 2 Test:
- Solving equations: Students should be able to solve linear equations with one variable and equations involving fractions and decimals.
- Inequalities: Students should understand how to solve and graph linear inequalities.
- Systems of equations: Students should be able to solve systems of two linear equations by substitution, elimination, or graphing.
- Linear functions: Students should understand the concept of a linear function, be able to graph linear functions, and find the slope and y-intercept of a line.
- Applications of algebra: Students should be able to apply algebraic concepts to real-world situations, such as solving problems involving rates, distances, and mixtures.
The Algebra 1 Unit 2 Test serves as an important checkpoint for students and instructors to assess their progress and identify areas that may require additional attention and review. It helps determine if students have mastered the foundational skills and concepts necessary to progress in their algebra studies.
Preparing for the Algebra 1 Unit 2 Test involves reviewing class notes, completing practice problems, and seeking clarification on any challenging concepts. It is also helpful to work through previous homework assignments and quizzes to reinforce understanding and build confidence.
Why is Algebra 1 Unit 2 Test Important

Algebra 1 Unit 2 test is an important milestone in a student’s mathematics education. This test is crucial for several reasons. Firstly, it assesses the student’s understanding and mastery of the fundamental concepts and skills learned in the second unit of Algebra 1. It evaluates their ability to solve equations, simplify expressions, and apply mathematical principles to real-world problems.
Secondly, the Algebra 1 Unit 2 test provides valuable feedback to both the student and the teacher. It highlights the areas where the student may be struggling or need additional support. This feedback allows the teacher to tailor their instruction and provide targeted interventions to help the student improve their understanding and performance.
Additionally, the Algebra 1 Unit 2 test contributes to the overall assessment of the student’s mathematical proficiency. It helps to determine whether the student is meeting the learning objectives outlined in the curriculum and whether they are ready to progress to the next unit or level of mathematics.
Furthermore, the results of the Algebra 1 Unit 2 test can have an impact on the student’s academic record and future opportunities. A strong performance on this test can demonstrate the student’s competence in algebraic reasoning and problem-solving, which are essential skills for success in higher-level mathematics courses and many STEM-related fields.
In conclusion, the Algebra 1 Unit 2 test is important because it assesses the student’s mastery of fundamental algebraic concepts, provides valuable feedback for improvement, contributes to the overall assessment of mathematical proficiency, and can have an impact on future academic and career opportunities.
Key Concepts Covered in Algebra 1 Unit 2 Test

In the Algebra 1 Unit 2 Test, students are assessed on their understanding of key concepts related to algebraic expressions, equations, and inequalities. This unit builds on the foundational knowledge from Unit 1, where students learned about the order of operations, properties of real numbers, and solving simple equations.
One of the key concepts covered in the test is solving linear equations and inequalities. Students are expected to be able to solve equations with one variable, using methods such as addition, subtraction, multiplication, and division. They should also be able to identify solutions to systems of equations and represent solutions graphically.
Another important topic covered in the test is simplifying algebraic expressions. Students should be able to combine like terms, apply the distributive property, and simplify expressions with multiple variables. They should also be able to identify and use properties of exponents and rational exponents.
The test also assesses students’ ability to solve word problems involving algebraic equations and inequalities. Students should be able to translate verbal descriptions of situations into mathematical expressions or equations, and then solve them to find the unknown variables.
Overall, the Algebra 1 Unit 2 Test evaluates students’ understanding of fundamental algebraic concepts, their ability to solve equations and inequalities, and their proficiency in working with algebraic expressions. Mastery of these key concepts is crucial for success in higher-level algebra courses and other math-related subjects.
Linear Equations and Inequalities
In algebra, linear equations and inequalities are essential concepts that help us solve problems involving unknowns. A linear equation is an equation in which the highest power of the variable is one. It can be written in the form “ax + b = 0”, where “a” and “b” are constants and “x” is the variable. Solving a linear equation involves finding the value of the variable that makes the equation true.
Linear inequalities, on the other hand, involve inequalities instead of equations. They can be written in the form “ax + b < c" or "ax + b > c”, where “a”, “b”, “c” are constants and “x” is the variable. Solving a linear inequality involves finding the range of values for the variable that make the inequality true. This range can be represented graphically on a number line.
To solve linear equations and inequalities, we can use various methods such as the addition method, the substitution method, or the graphing method. These methods help us simplify the equations or inequalities and isolate the variable. By solving them, we can find the solutions or the range of values that satisfy the given equation or inequality.
Linear equations and inequalities have numerous real-life applications such as calculating distances, determining rates of change, or solving optimization problems. They provide a foundation for more advanced topics in algebra and are used extensively in fields such as physics, engineering, finance, and computer science.
Systems of Linear Equations
A system of linear equations consists of two or more equations that are solved simultaneously to find the values of the variables that satisfy all the equations. Each equation in the system represents a line in a coordinate plane, and the solution to the system is the point(s) where these lines intersect.
In algebra, systems of linear equations are typically solved using various methods, including substitution, elimination, and graphing. These methods involve manipulating the equations to isolate one variable and then substituting that value into another equation to find the value(s) of the other variable(s).
Substitution: In this method, one equation is solved for one variable in terms of the other variable, and then that expression is substituted into the other equation. This allows for the determination of the value of one variable, which can then be used to find the value of the other variable.
Elimination: This method involves adding or subtracting equations to eliminate one variable. The goal is to create a new equation with only one variable, which can then be solved to find its value. This value can then be substituted back into one of the original equations to find the value of the other variable.
Graphing: When the system consists of two linear equations, they can be graphed on the coordinate plane. The point(s) of intersection between the two lines represent the solution(s) to the system. This method is useful for visually understanding the solution to the system, especially when dealing with non-linear systems.
In conclusion, systems of linear equations provide a powerful tool for solving problems that involve multiple variables and relationships between them. By applying appropriate techniques, such as substitution, elimination, or graphing, we can find the solution(s) to these systems, enabling us to analyze and interpret the given information effectively.
Preparation Tips for Algebra 1 Unit 2 Test
Preparing for the Algebra 1 Unit 2 test can be challenging, but with the right strategies, you can improve your chances of success. Here are some tips to help you prepare effectively:
1. Review the material thoroughly: Start by going through all the notes, examples, and textbook chapters covered in Unit 2. Make sure you understand the key concepts, equations, and formulas. Practice solving a variety of problems to strengthen your understanding.
2. Create a study plan: Divide your study time into manageable chunks and create a schedule that allows you to review all the topics. Allocate more time for areas where you feel less confident. Avoid cramming the night before the test, as it can lead to fatigue and anxiety.
3. Seek help if needed: If you’re struggling with any specific concept or topic, don’t hesitate to ask for help. Consult your teacher, classmates, or online resources for additional explanations and practice problems. Understanding the fundamentals is key to succeeding in Algebra.
4. Practice with previous tests and quizzes: Use previous tests, quizzes, and homework assignments as practice material. This will give you an idea of the types of questions that may appear on the test and help you identify areas where you need more practice.
5. Review sample problems: Look for sample problems online or in your textbook that are similar to those you expect to see on the test. Practice solving them using the appropriate methods and formulas. This will help you become familiar with the problem-solving process and build confidence.
6. Quiz yourself: Create flashcards or a set of practice questions and quiz yourself regularly. This will help reinforce your understanding of the material and improve your retention of key concepts and formulas.
7. Get plenty of rest and eat well: Make sure to get enough sleep the night before the test and eat a balanced meal. A well-rested and nourished brain functions better and will help you stay focused during the test.
By following these tips and putting in consistent effort, you can feel more confident and prepared for the Algebra 1 Unit 2 test. Remember that practice and understanding are key to success in algebra!