
Understanding angle terminology is crucial when it comes to solving mathematical problems involving angles. In geometry, angles are an essential concept that is used to describe the relationship between lines, shapes, and points. By using specific equations, we can determine the measurements and properties of angles.
One important angle terminology is the degree of an angle. The degree is a unit of measurement that represents the amount of rotation between two lines that meet at a common point. A full circle is divided into 360 degrees, with each degree representing 1/360th of the circle’s total rotation. By knowing the degree measurement of an angle, we can accurately describe its size and compare it to other angles.
Another useful angle equation is the angle sum property. This property states that the sum of the measures of the angles in a triangle is always 180 degrees. For example, if we have a triangle with angle A measuring 50 degrees and angle B measuring 70 degrees, we can find the measure of angle C by subtracting the sum of angle A and angle B from 180 degrees. This equation allows us to solve for unknown angles in different geometric shapes.
Additionally, the concept of supplementary and complementary angles is essential in geometry. Supplementary angles are two angles that, when combined, form a straight line and measure 180 degrees. Complementary angles, on the other hand, are two angles that, when added together, measure 90 degrees. By using these angle relationships, we can solve equations and find missing angle measurements.
In conclusion, understanding angle terminology and equations is vital in solving mathematical problems involving angles. By knowing the degree measurement, angle sum property, and the concepts of supplementary and complementary angles, we can accurately describe and solve for unknown angles in various geometric shapes.
Understanding Angle Terminology
In geometry, angles play a crucial role in understanding the relationships between different shapes and objects. To fully comprehend angle terminology, it is essential to grasp the basic concepts and definitions associated with angles.
An angle is formed by two rays or line segments with a common endpoint, called the vertex. The two rays are referred to as the sides of the angle. The measure of an angle is determined by the amount of rotation between the two rays, and it is usually expressed in degrees, radians, or revolutions. Understanding the different types of angles is fundamental in geometry.
Types of Angles:

- Acute angle: An acute angle is an angle that measures less than 90 degrees. It is a sharp angle.
- Right angle: A right angle measures exactly 90 degrees. It forms a perfect L-shape and is often denoted by a small square in the vertex.
- Obtuse angle: An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees. It is a wide angle.
- Straight angle: A straight angle is a flat angle that measures exactly 180 degrees. It forms a straight line.
- Reflex angle: A reflex angle measures more than 180 degrees but less than 360 degrees. It is an angle that “bends backward.”
- Complementary angles: Complementary angles are two angles whose sum is 90 degrees. When combined, they form a right angle.
- Supplementary angles: Supplementary angles are two angles whose sum is 180 degrees. When combined, they form a straight angle.
Understanding and using these angle terminologies is essential in solving geometry problems and equations. Whether it’s measuring angles, identifying relationships between angles, or calculating missing angles, a solid understanding of angle terminology is crucial for success in geometry.
Definition of Angle
An angle is formed when two rays meet at a common endpoint called the vertex. The rays are usually represented by lines, and the vertex is the point where the lines intersect. In geometry, angles are measured in degrees or radians and can be classified based on their measurements.
Types of Angles:
1. Acute angle: An acute angle is less than 90 degrees. It is sharp and smaller than a right angle.
2. Right angle: A right angle measures exactly 90 degrees. It forms a perfect L shape and is often found in squares and rectangles.
3. Obtuse angle: An obtuse angle is greater than 90 degrees but less than 180 degrees. It is larger than a right angle and forms a wide V shape.
4. Straight angle: A straight angle measures exactly 180 degrees. It forms a straight line and is often found in line segments.
5. Reflex angle: A reflex angle measures greater than 180 degrees but less than 360 degrees. It extends beyond a straight angle.
6. Complementary angles: Two angles are complementary if their measures add up to 90 degrees. For example, if one angle measures 30 degrees, the other angle will be 60 degrees to make a total of 90 degrees.
7. Supplementary angles: Two angles are supplementary if their measures add up to 180 degrees. For example, if one angle measures 120 degrees, the other angle will be 60 degrees to make a total of 180 degrees.
Angles play a crucial role in various fields such as geometry, trigonometry, physics, and engineering. They are used to measure and describe the orientation and position of objects, determine distances and angles in triangles, and solve various mathematical problems.
Types of Angles
Angles are an important concept in geometry. They are formed when two rays intersect at a common endpoint, called a vertex. Angles can be classified into different types based on their measurements and relationships with other angles.
1. Acute Angle: An acute angle is an angle that measures less than 90 degrees. It is a small angle that is sharp and narrow.
2. Right Angle: A right angle is an angle that measures exactly 90 degrees. It forms a perfect L-shape and is often found in squares and rectangles.
3. Obtuse Angle: An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees. It is a wider angle that is open and blunt.
4. Straight Angle: A straight angle is an angle that measures exactly 180 degrees. It forms a straight line and is often found in line segments.
5. Reflex Angle: A reflex angle is an angle that measures more than 180 degrees but less than 360 degrees. It is a wide angle that extends beyond a straight line.
6. Complementary Angles: Complementary angles are two angles whose sum is 90 degrees. They form a right angle when combined.
7. Supplementary Angles: Supplementary angles are two angles whose sum is 180 degrees. They form a straight angle when combined.
8. Vertical Angles: Vertical angles are formed by the intersection of two lines and are opposite each other. They have equal measures.
Understanding the different types of angles is essential in solving geometry problems and analyzing shapes and figures. Knowing their properties and relationships can help in measuring and constructing angles accurately.
Measuring Angles
Angles are geometric figures that can be measured and classified based on their size and position. They play a crucial role in various fields, including mathematics, physics, and engineering.
When measuring angles, it is essential to use the correct tools, such as a protractor or a angle measuring device, to ensure accurate results. The most common unit for measuring angles is degrees, denoted by the symbol °. A complete revolution or a full circle is 360°, while a right angle measures 90°.
Types of Angles:
- Acute Angle: An acute angle measures less than 90°.
- Obtuse Angle: An obtuse angle measures between 90° and 180°.
- Right Angle: A right angle measures exactly 90°.
- Straight Angle: A straight angle measures exactly 180°.
- Reflex Angle: A reflex angle measures between 180° and 360°.
Angles can also be classified based on their position. For example, two angles are considered adjacent angles if they share a common vertex and a common side but do not overlap. Vertical angles are formed by the intersection of two lines and are opposite to each other. Complementary angles add up to 90°, while supplementary angles add up to 180°.
In conclusion, understanding and measuring angles is crucial in various disciplines. By using the appropriate tools and understanding the different types and classifications, we can accurately measure and analyze angles in a wide range of applications.
Angle Relationships
Angles are an important concept in geometry, and understanding the relationships between different angles is crucial for solving mathematical problems. There are several types of angle relationships that can be identified based on their positions and measurements.
One important relationship is that of complementary angles. Complementary angles are two angles that add up to 90 degrees. For example, if angle A measures 30 degrees, then angle B must measure 60 degrees in order to be complementary. Complementary angles are often found in right triangles, where one angle is always 90 degrees.
Another type of angle relationship is that of supplementary angles. Supplementary angles are two angles that add up to 180 degrees. For example, if angle C measures 120 degrees, then angle D must measure 60 degrees in order to be supplementary. Supplementary angles are often found in parallel lines, where corresponding angles are equal.
Adjacent angles are angles that share a common vertex and a common side but do not overlap. They are often found in polygons, where sides intersect at vertices. If angle E measures 40 degrees and angle F measures 50 degrees, then they are adjacent angles.
These are just a few examples of the different angle relationships that can be identified. By understanding these relationships and using the appropriate equations, delta math can help solve problems related to angles and geometry.
Complementary Angles
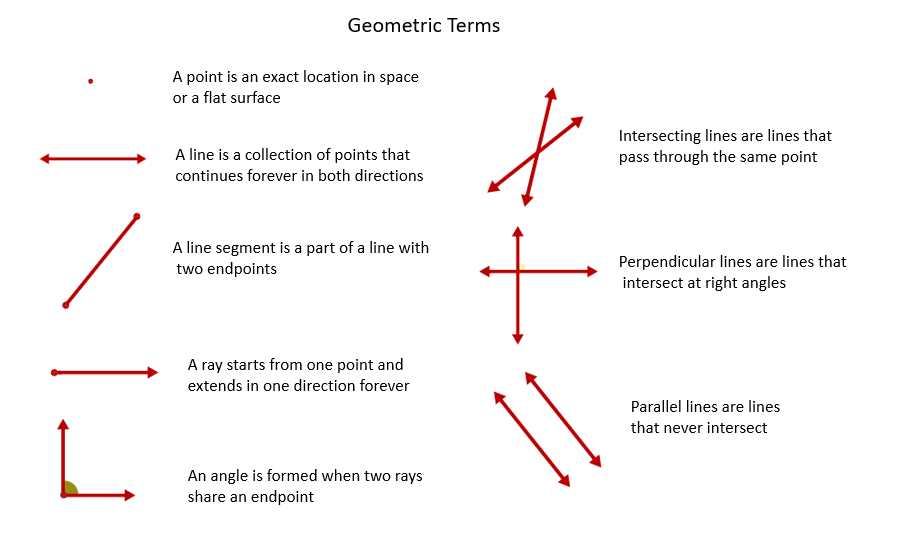
In the field of mathematics, angles are often classified based on their relationships with other angles. One such classification is complementary angles. Complementary angles are two angles whose measures sum up to 90 degrees. In other words, when you add up the measurements of two complementary angles, the result is always 90 degrees.
Complementary angles can be found in various geometric figures and situations. For example, in a right triangle, one angle is always 90 degrees, which means that the other two angles are complementary. Similarly, in a rectangle, opposite angles are always complementary. In addition, when two lines intersect, the angles formed on opposite sides of the intersection are also complementary.
Complementary angles can be represented by equations and solved algebraically. Let’s say we have an angle x. Its complement can be represented as 90 – x. By setting up an equation, such as x + (90 – x) = 90, we can solve for the values of x and its complement. This allows us to find the measures of complementary angles even if we are only given the measure of one angle.
Understanding complementary angles is important in various mathematical applications, such as trigonometry, geometry, and solving equations involving angles. By recognizing and utilizing the concept of complementary angles, mathematicians and scientists can work with angles more efficiently and accurately in their calculations and problem-solving.
Supplementary Angles

Supplementary angles are a pair of angles whose measures add up to 180 degrees. This means that when you add the measures of two supplementary angles together, the sum will always be equal to 180 degrees.
A supplementary angle can be formed by combining two angles that are adjacent or non-adjacent, as long as their measures add up to 180 degrees. For example, if angle A measures 80 degrees, then its supplementary angle, angle B, will measure 100 degrees, because 80 + 100 = 180.
Supplementary angles are useful in many areas of geometry and trigonometry. They can be used to find missing angle measures in a triangle or to determine the angle of inclination in a right triangle. In addition, supplementary angles can be used to solve equations involving angle measurements.
When working with supplementary angles, it is important to remember that the sum of their measures will always be 180 degrees. This property can be used to set up equations and solve for missing angles in a variety of geometric problems.
Overall, understanding supplementary angles and their properties is essential for solving problems involving angle measurements and equations in geometry and trigonometry.
Vertical Angles
Vertical angles are a special type of angles that are formed when two lines intersect. These angles have equal measures and are located opposite each other. They are commonly denoted as angle A and angle B.
Vertical angles are important in geometry because they have several properties. First, vertical angles are always congruent, which means they have the same measurement. This property can be represented by the equation A = B, where A represents the measure of one angle and B represents the measure of the other angle.
Another property of vertical angles is that their measures add up to 180 degrees. This can be represented by the equation A + B = 180. This property is useful in solving problems involving vertical angles.
A practical example of vertical angles can be seen when two streets intersect. The angles formed by the streets are vertical angles. If one angle measures 60 degrees, then the angle opposite it will also measure 60 degrees. Additionally, the sum of these two angles will be 180 degrees.
Understanding vertical angles is important in geometry as it helps in solving various problems related to angles. Knowing their properties and how to find their measures can be useful in calculating unknown angles, especially in complex geometric shapes.
Adjacent Angles
Adjacent angles are two angles that have a common vertex and a common side between them. They are also known as neighboring angles. In other words, adjacent angles are angles that share a corner and a side.
When two lines intersect, they form four angles at the point of intersection. The angles that are next to each other, or adjacent, are called adjacent angles. These angles can be found on the same line or on different lines.
Adjacent angles can be categorized into two types: adjacent supplementary angles and adjacent complementary angles.
Adjacent supplementary angles are two angles that add up to 180 degrees. For example, if angle A and angle B are adjacent supplementary angles, then the measure of angle A + measure of angle B = 180 degrees.
Adjacent complementary angles are two angles that add up to 90 degrees. For example, if angle C and angle D are adjacent complementary angles, then the measure of angle C + measure of angle D = 90 degrees.
Adjacent angles are important in geometry because they help us understand the relationship between angles formed by intersecting lines. They also help us solve problems involving angles, such as finding unknown angles or proving geometric theorems.