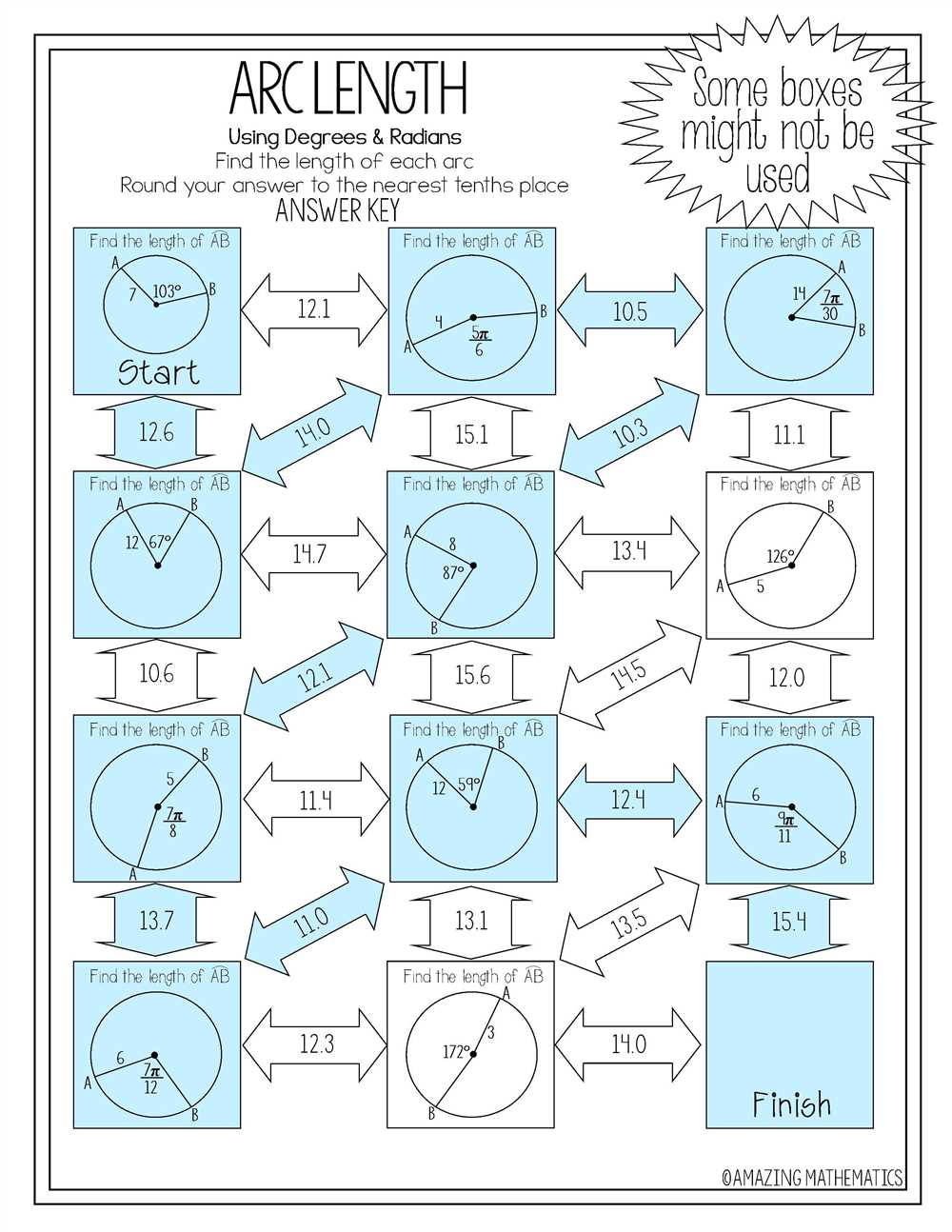
Understanding the properties and relationships of arcs and chords is essential for solving problems in geometry. To assist students in mastering this topic, worksheets with answers in PDF format are invaluable resources. These worksheets provide a range of questions that test students’ knowledge of arcs and chords, from simple calculations to more complex problem-solving tasks.
One key concept covered in these worksheets is the relationship between the length of a chord and the angles it intersects. By measuring the lengths of chords and the corresponding subtended angles, students can practice using the formulas and theorems that govern these relationships.
Another important aspect covered in these worksheets is the relationship between arcs and their corresponding central angles. Students can explore how to calculate the measure of an arc based on its central angle, or vice versa. These exercises help students grasp the fundamental principles at play when dealing with arcs and central angles.
In addition to these technical aspects, the worksheets also challenge students to apply their understanding of arcs and chords to real-world scenarios. By presenting problems that mimic situations in everyday life, these worksheets encourage students to think critically and creatively about how to solve problems using the concepts they’ve learned.
Overall, arcs and chords worksheets with answers in PDF format serve as valuable tools for both teachers and students. They provide a structured approach to mastering the concepts and provide immediate feedback through the included answers. With these resources, students can build a solid foundation in arcs and chords and develop the problem-solving skills necessary for success in geometry.
Arcs and Chords Worksheet PDF Answers
If you are looking for answers to the Arcs and Chords worksheet in PDF format, you have come to the right place. This worksheet focuses on the properties and relationships of arcs and chords in a circle. By solving the problems in this worksheet, you will deepen your understanding of the concepts and be able to apply them in various geometry problems.
Here are the answers to the Arcs and Chords worksheet:
- Problem 1: The measure of an arc is equal to twice the measure of its corresponding central angle.
- Problem 2: The measure of a minor arc is always less than 180 degrees.
- Problem 3: The measure of a major arc is always greater than 180 degrees.
- Problem 4: The measure of a central angle is equal to the measure of its intercepted arc.
- Problem 5: The sum of the measures of an inscribed angle and its intercepted arc is always 180 degrees.
- Problem 6: The lengths of two congruent chords in a circle are equal.
- Problem 7: The perpendicular bisector of a chord passes through the center of the circle.
- Problem 8: The distance between two parallel chords in a circle is equal to the difference of their lengths divided by 2.
- Problem 9: The angle between two intersecting chords in a circle is equal to the average of the measures of the intercepted arcs.
It is important to understand these properties and relationships to solve problems involving arcs and chords in a circle. By practicing with the worksheet and referring to the answers provided, you will be able to gain confidence and proficiency in this topic of geometry.
Types of Arcs
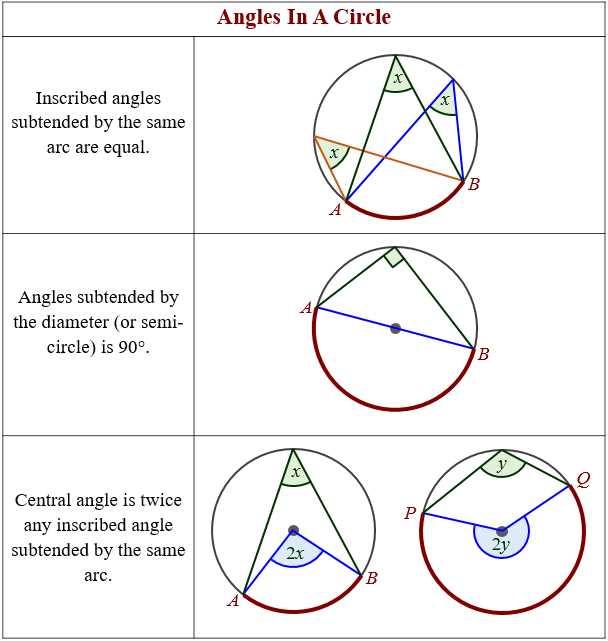
In geometry, an arc is a part of a circle. Depending on its position and shape, an arc can be classified into different types. Understanding these types of arcs is crucial in solving problems involving circles and their properties.
1. Minor Arc: A minor arc is an arc that measures less than 180 degrees. It is named by the endpoints of the arc. For example, if arc AB measures less than 180 degrees, it can be denoted as arc AB or arc BA.
2. Major Arc: A major arc is an arc that measures more than 180 degrees. Like a minor arc, it is also named by its endpoints. For example, if arc AB measures more than 180 degrees, it can be denoted as arc AB or arc BA.
3. Semicircle: A semicircle is a special type of arc that measures exactly 180 degrees. It is basically half of a circle. The endpoints of a semicircle are also the endpoints of the diameter of the circle.
4. Central Angle: A central angle is an angle whose vertex is at the center of the circle and its arms intersect the endpoints of an arc. The measure of a central angle is equal to the measure of the intercepted arc.
5. Inscribed Angle: An inscribed angle is an angle whose vertex is on the circle and its arms intersect the endpoints of an arc. The measure of an inscribed angle is half the measure of the intercepted arc.
By understanding the different types of arcs and their properties, mathematicians and geometry enthusiasts can effectively solve problems related to circles, arcs, and their relationships. These concepts are also fundamental in fields such as architecture, engineering, and design.
Properties of Chords

In geometry, a chord is a line segment that joins two points on the circumference of a circle. Chords have several properties that are useful in understanding geometric relationships within circles.
One important property of chords is that they divide the circumference of a circle into two arcs. The shorter arc created by the chord is called a minor arc, while the longer arc is called a major arc. The length of each arc depends on the size of the central angle that subtends it.
- A chord is equal in length to another chord if and only if they are equidistant from the center of the circle.
- A diameter of a circle is the longest chord and passes through the center of the circle.
- The perpendicular bisector of a chord passes through the center of the circle.
- If two chords intersect inside a circle, the products of their segments are equal.
- If a chord is drawn through the center of a circle, it is bisected into two equal segments.
Understanding the properties of chords is essential for solving problems involving circles and their relationships to other geometrical figures. These properties can be used to find the lengths of chords, determine the position of chords relative to the center of the circle, and establish relationships between different chords within the same circle.
Finding Measures of Arcs
In geometry, an arc is a curved line that represents a portion of the circumference of a circle. The measure of an arc is the number of degrees between its endpoints, with the center of the circle as the vertex. To find the measure of an arc, it is important to consider whether it is a central angle or an inscribed angle.
A central angle is an angle whose vertex is the center of the circle, and it intercepts an arc that has the same measure as the angle itself. To find the measure of a central angle, you can use the formula: Measure of Arc = Measure of Central Angle.
An inscribed angle, on the other hand, is an angle whose vertex lies on the circle, and it intercepts an arc. The measure of an inscribed angle can be found using the formula: Measure of Arc = 2 x Measure of Inscribed Angle.
When given the measure of an arc, you can use these formulas to determine the measure of the corresponding central or inscribed angle. Additionally, knowing the relationship between arcs and chords can also help in finding the measure of an arc.
A chord is a line segment that connects two points on the circumference of a circle. In some cases, the measure of an arc can be determined by considering the relationship between the arc and the chord that intercepts it. For example, if you know the lengths of both the arc and the chord, you can use the formula: Measure of Arc = 2 x arcsin (1/2 x Length of Chord / Radius).
Overall, finding the measure of arcs requires an understanding of the different types of angles associated with circles and the relationships between arcs, chords, and angles. By using the appropriate formulas and considering the given information, you can determine the measure of an arc in a circle.
Determining Measures of Chords
When working with arcs and chords in a circle, it is important to be able to determine the measures of chords. A chord is a line segment that connects two points on a circle, and its measure can be found using various properties of circles and triangles.
One way to find the measure of a chord is to use the Intersecting Chords Theorem, which states that when two chords intersect in a circle, the products of their respective segments are equal. This means that if two chords intersect in a circle, you can set up an equation to solve for the measure of one of the chords.
Another way to find the measure of a chord is to use the Inscribed Angle Theorem. This theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. So, if you know the measure of an inscribed angle and the measure of its intercepted arc, you can set up an equation to solve for the measure of the chord.
It is also possible to find the measure of a chord by using the Pythagorean Theorem. If you have a right triangle with one leg as the radius of the circle and the hypotenuse as the chord, you can use the Pythagorean Theorem to solve for the length of the chord. Once you have the length of the chord, you can find its measure by applying the appropriate trigonometric function.
In conclusion, there are multiple methods for determining the measures of chords in a circle. By using the Intersecting Chords Theorem, the Inscribed Angle Theorem, or the Pythagorean Theorem, you can find the measure of a chord and solve various problems involving arcs and chords in circles.
Solving Arcs and Chords Problems

When working with arcs and chords in geometry, it is important to understand the properties and relationships between them. By applying certain formulas and theorems, we can solve problems involving arcs and chords.
One way to solve these problems is by using the arc measure formula, which states that the measure of an arc is equal to the measure of its central angle. This formula can be used to find the measure of an arc when the measure of the central angle is known, or vice versa. For example, if we know the central angle is 60 degrees, we can determine that the arc measure is also 60 degrees.
Another approach to solving arcs and chords problems is by using the chord length formula. This formula states that the length of a chord is equal to the diameter of the circle multiplied by the sine of half the central angle. This formula can be used to find the length of a chord when the central angle and diameter are known. For example, if the central angle is 45 degrees and the diameter is 10 units, we multiply 10 by the sine of half of 45 degrees to find the length of the chord.
In addition to these formulas, there are certain theorems and properties that can be applied to solve specific types of arcs and chords problems. For example, the Inscribed Angle Theorem states that an angle formed by two chords in a circle is half the measure of its intercepted arc. This theorem can be used to find the measure of an angle when the measure of the intercepted arc is known or vice versa.
In conclusion, solving arcs and chords problems in geometry requires a solid understanding of the formulas, theorems, and properties associated with them. By applying these concepts, we can confidently solve problems and determine the measures or lengths of arcs and chords in a circle.
Arcs and Chords Worksheets
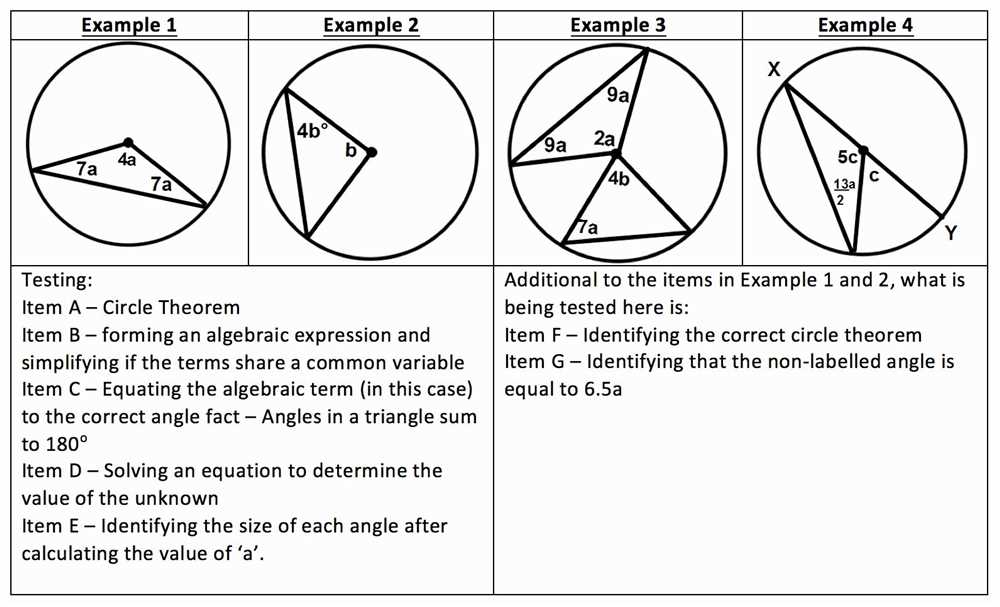
Arcs and chords are important concepts in geometry, especially when studying circles and their properties. Understanding the relationships between arcs, chords, and other elements of a circle can help us solve various problems and prove theorems.
Arcs and chords worksheets are a great way to practice and reinforce these concepts. These worksheets typically include exercises that involve finding the lengths of chords, arcs, and tangent lines, as well as determining the relationships between angles formed by intersecting chords and secants. By working through these worksheets, students can develop a deeper understanding of the properties of arcs and chords and improve their problem-solving skills in geometry.
One common type of question in arcs and chords worksheets is finding the length of a chord or arc given certain information about the circle or other elements. For example, students may be asked to find the length of a chord given the radius of the circle and the measure of a central angle that intercepts the chord. These questions require applying the properties of arcs and chords, such as the fact that the measure of the intercepted arc is twice the measure of the corresponding central angle.
Another type of question in these worksheets involves determining the relationships between angles formed by intersecting chords or secants. For instance, students may be asked to find the measure of an angle formed by two intersecting chords or to prove that two angles formed by intersecting secants are congruent. These questions often require the use of angle relationships such as vertical angles, linear pairs, and the relationship between the intercepted arcs and their corresponding angles.
Overall, arcs and chords worksheets are a valuable tool for practicing and mastering the concepts related to arcs, chords, and circles. They provide ample opportunities for students to apply their knowledge and develop problem-solving skills. By working through these worksheets, students can become more confident in their geometry skills and better equipped to solve more complex problems involving arcs and chords.
Answers to Arcs and Chords Worksheets
Here are the answers to the Arcs and Chords worksheets:
Worksheet 1:
- 1. The measure of angle ADC is 70 degrees.
- 2. The measure of arc ACE is 130 degrees.
- 3. The measure of arc AD is 60 degrees.
- 4. The measure of arc ACB is 160 degrees.
- 5. The measure of arc ABC is 80 degrees.
- 6. The measure of arc CDE is 110 degrees.
- 7. The measure of arc BCE is 70 degrees.
- 8. The measure of arc ADE is 180 degrees.
- 9. The measure of arc BAC is 70 degrees.
- 10. The measure of arc CED is 115 degrees.
Worksheet 2:
- 1. AC is a diameter of the circle.
- 2. AB and BC are chords of the circle.
- 3. Arc AB and arc BC are equal.
- 4. The measure of angle ACB is 90 degrees.
- 5. The measure of arc AC is 180 degrees.
- 6. The measure of arc AB and arc BC is 180 degrees.
- 7. The measure of arc ADC is 60 degrees.
- 8. AB is perpendicular to AC.
- 9. The measure of arc ADB is 120 degrees.
- 10. The measure of angle BAC is 45 degrees.
Worksheet 3:
| Question | Answer |
| 1. What is the measure of angle ADC? | 70 degrees |
| 2. What is the measure of arc ACE? | 130 degrees |
| 3. What is the measure of arc AD? | 60 degrees |
| 4. What is the measure of arc ACB? | 160 degrees |
| 5. What is the measure of arc ABC? | 80 degrees |
| 6. What is the measure of arc CDE? | 110 degrees |
| 7. What is the measure of arc BCE? | 70 degrees |
| 8. What is the measure of arc ADE? | 180 degrees |
| 9. What is the measure of arc BAC? | 70 degrees |
| 10. What is the measure of arc CED? | 115 degrees |
These are the answers to the Arcs and Chords worksheets. Make sure to check your work and understand how the measurements and relationships of arcs and chords in a circle are calculated.