
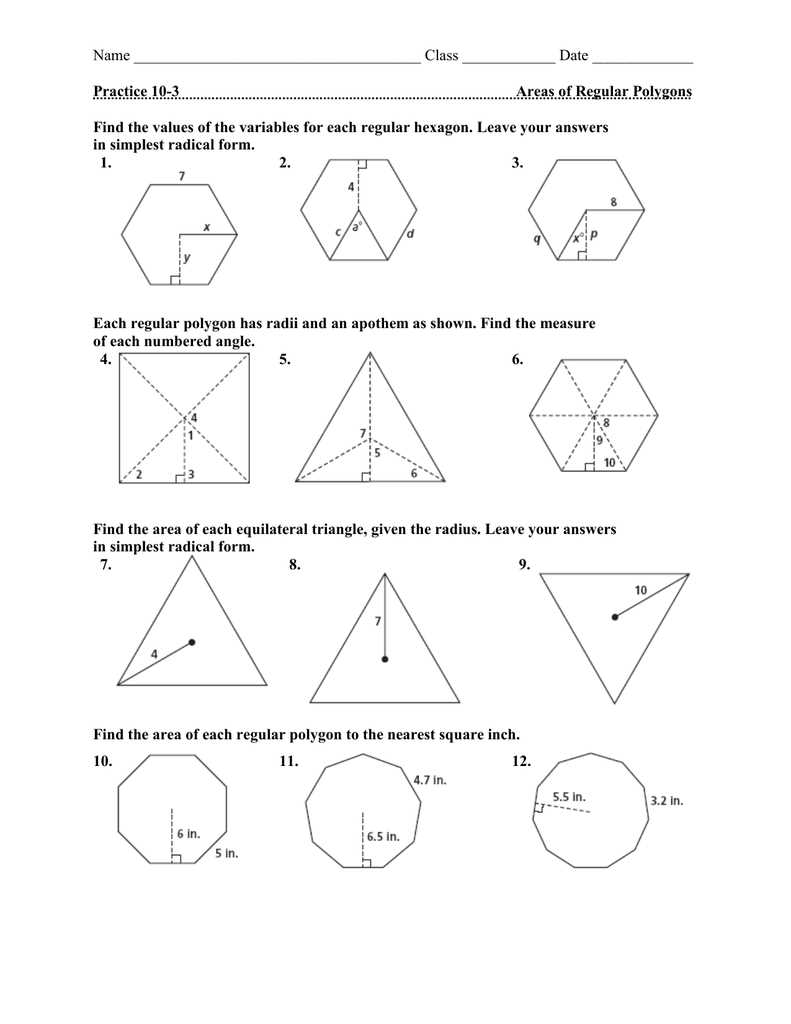
In the field of geometry, regular polygons are one of the fundamental concepts studied. These polygons have sides and angles that are all congruent, meaning they are equal in length and measure. To calculate the area of a regular polygon, one must know the length of its sides and the apothem, which is a line segment drawn from the center of the polygon to the midpoint of one of its sides. This worksheet, titled “Areas of Regular Polygons Worksheet 11 4 Answers,” provides students with practice problems to test their understanding of finding the area of regular polygons.
The worksheet consists of a series of questions where students are given the length of the side and the apothem of a regular polygon. They are then required to calculate the area of the polygon using the given information. By solving these problems, students will strengthen their skills in calculating the area of regular polygons and reinforce their understanding of the relationship between side length, apothem, and area.
Answering the questions on this worksheet will also help students apply their knowledge of geometry to real-world situations. Regular polygons can be found in various objects and structures, such as floor tiles, honeycombs, and window panes. Being able to calculate the area of these polygons is essential in fields such as architecture, engineering, and design. By completing this worksheet, students will develop the analytical thinking and problem-solving skills required in these professions.
In conclusion, the “Areas of Regular Polygons Worksheet 11 4 Answers” provides students with an opportunity to practice calculating the area of regular polygons. By solving the problems on this worksheet, students will reinforce their understanding of the concept and develop the skills necessary for real-world applications. So, grab a pencil and get ready to tackle some geometry problems!
Areas of Regular Polygons Worksheet 11 4 Answers
In the study of geometry, regular polygons play a significant role, and calculating their areas is an essential skill. Worksheet 11 4 focuses on finding the areas of regular polygons with different numbers of sides.
The worksheet begins with a set of exercises that require students to find the side lengths of regular polygons using the given information. By using formulas and geometric reasoning, students can determine the lengths of the sides. This step is crucial for later calculations of the area.
To find the area of a regular polygon, there are different formulas depending on the number of sides. The worksheet covers regular polygons with 3, 4, 5, 6, and 8 sides. Students are prompted to apply the appropriate formula for each polygon and calculate the area using the given side lengths.
The answers for the worksheet are provided, allowing students to check their work and ensure they have made the correct calculations. By comparing their answers with the given solutions, students can identify any mistakes and understand the correct approach for finding the areas of regular polygons.
Working through the Areas of Regular Polygons Worksheet 11 4 helps students develop their geometry skills and reinforce their understanding of regular polygons and their properties. By practicing and applying the formulas, students can become proficient in calculating the areas of regular polygons with different numbers of sides.
Understanding Regular Polygons
Regular polygons are geometric shapes that have equal sides and equal angles. They are formed by connecting the vertices of a circle with straight lines. Regular polygons are commonly found in various fields of study, including mathematics, architecture, and nature.
One key aspect of understanding regular polygons is knowing how to identify and classify them. A regular polygon can be identified by the number of sides it has. For example, a triangle is a regular polygon with three sides, while a square is a regular polygon with four sides. As the number of sides increases, the polygon becomes more complex, with names such as pentagon (five sides), hexagon (six sides), heptagon (seven sides), and so on.
Another important concept to grasp is the relationship between the angle measures and the number of sides in a regular polygon. Each angle of a regular polygon is equal, which means that the total interior angle sum can be found by multiplying the number of sides minus two by 180 degrees. For example, a triangle has three sides, so the sum of its interior angles is (3 – 2) * 180 = 180 degrees.
Understanding regular polygons can be beneficial in various practical applications. In architecture, regular polygons are often used as the basis for designing buildings and structures. In nature, regular polygons can be observed in the arrangement of honeycomb cells in beehives or the geometric patterns of certain plants. Additionally, in mathematics, regular polygons are studied to understand symmetry, tessellations, and other geometric properties.
Formulas for Calculating Area
When it comes to calculating the area of different shapes, there are specific formulas that can be used. These formulas are essential in determining the amount of space occupied by a particular shape, whether it is a regular polygon or an irregular shape.
For regular polygons, the area can be calculated using the formula:
Area = 0.5 * apothem * perimeter
Here, the apothem is the distance from the center of the polygon to the midpoint of any side, and the perimeter is the total length of all the sides of the polygon.
For example, in the case of a regular triangle, the apothem and perimeter can be easily determined, allowing us to calculate the area using the formula mentioned above.
On the other hand, when dealing with irregular shapes, the area can be calculated using different methods such as breaking the shape into smaller regular shapes and summing up their individual areas or by using advanced integration techniques.
It is essential to have a good understanding of these area formulas as they can be applied to various real-life situations such as determining the size of a field, estimating the amount of paint needed for a wall, or even calculating the surface area of a complex three-dimensional object.
- Regular Polygon Formula: Area = 0.5 * apothem * perimeter
- Irregular Shape Formula: Breaking down into smaller regular shapes or using advanced integration techniques.
- Applications in real-life situations: Field measurement, painting estimation, surface area calculations.
Special Cases: Equilateral Triangles and Squares
An equilateral triangle is a special type of triangle where all three sides are of equal length. In an equilateral triangle, all three angles are also equal, measuring 60 degrees each. This unique property makes calculations involving equilateral triangles relatively simple.
When finding the area of an equilateral triangle, we can use the formula: Area = (s^2 * √3) / 4, where “s” represents the length of one side of the triangle.
A square is another special case of a regular polygon. It is a quadrilateral with all four sides of equal length and all four angles equal to 90 degrees. The properties of a square make it easier to calculate its area compared to other polygons.
The formula for finding the area of a square is straightforward: Area = s^2, where “s” represents the length of one side of the square.
Equilateral triangles and squares are commonly used shapes in various fields, including architecture, geometry, and design. Understanding their specific properties and formulas for finding their areas is essential for solving problems and making accurate measurements in these fields.
Finding the Apothem
The apothem is an important measurement in the study of regular polygons. It refers to the distance from the center of the polygon to the midpoint of any side. Finding the apothem is crucial in various calculations involving regular polygons, such as finding the area or perimeter.
To find the apothem of a regular polygon, you can use different methods depending on the given information. One common method is to use the trigonometric ratios. By knowing the length of one side and the measure of one angle, you can apply trigonometric functions like sine, cosine, or tangent to find the apothem.
Example:
Suppose we have a regular hexagon with a side length of 8 units. To find the apothem, we can start by dividing the hexagon into six congruent equilateral triangles. Each triangle will have a side length of 8 units. By drawing a perpendicular line from the center of the hexagon to one of the sides, we can create a right triangle.
We can then use the trigonometric ratio of sine to find the apothem. The sine of the central angle, which is 60 degrees in this case, is equal to the opposite side (the apothem) divided by the hypotenuse (the side length of the equilateral triangle). Solving for the apothem, we get:
- sin(60 degrees) = opposite/hypotenuse
- sin(60 degrees) = apothem/8
- apothem = 8 * sin(60 degrees)
- apothem ≈ 6.93 units
Therefore, the apothem of this regular hexagon is approximately 6.93 units.
Another method to find the apothem is by using the formula:
apothem = (side length) / (2 * tan(180 degrees / number of sides))
This formula can be applied to any regular polygon, provided that the side length and number of sides are known.
Overall, finding the apothem is an essential step in solving problems related to regular polygons. It allows us to determine various measurements and properties of these polygons, contributing to a deeper understanding of their geometrical characteristics.
Using Trigonometry

Trigonometry is a branch of mathematics that deals with relationships between the angles and sides of triangles. It is a useful tool in various fields, including engineering, physics, and navigation. By using trigonometric functions such as sine, cosine, and tangent, we can solve problems involving right triangles and apply these concepts to other shapes and polygons.
When it comes to working with regular polygons, trigonometry can help us find the area, perimeter, and other properties of these shapes. For example, if we know the length of one side of a regular polygon and the measure of one of its interior angles, we can use trigonometry to calculate the length of the other sides and the area of the polygon.
Key trigonometric formulas for regular polygons:
- The interior angle of a regular polygon can be calculated using the formula: angle = (n-2) * 180 / n, where n is the number of sides of the polygon.
- The length of one side of a regular polygon can be determined using the formula: side length = (2 * radius) * sin(pi/n), where radius is the distance from the center of the polygon to one of its vertices.
- The area of a regular polygon can be found using the formula: area = (1/2) * (side length) * (apothem), where apothem is the distance from the center of the polygon to the midpoint of one of its sides.
By applying these formulas and utilizing the principles of trigonometry, we can solve various problems related to regular polygons, such as finding the area of a hexagon or the perimeter of an octagon.
Applying the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry that allows us to find the length of one side of a right triangle when the lengths of the other two sides are known. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Applying the Pythagorean Theorem involves identifying a right triangle within a given problem and using the theorem to find the missing side length. This theorem is especially useful when dealing with real-world applications such as distance calculations, construction projects, and navigation.
To apply the Pythagorean Theorem, we need to label the sides of the right triangle. The longest side, also known as the hypotenuse, is typically labeled as “c”. The other two sides are labeled as “a” and “b”. Using these labels, the theorem can be written as:
c² = a² + b²
Once we have identified the right triangle and labeled its sides, we can substitute the known side lengths into the formula. By rearranging the equation, we can solve for the missing side length. This allows us to calculate distances, determine the lengths of sides in irregular shapes, and solve a variety of other geometric problems.
Understanding and applying the Pythagorean Theorem is an essential skill in geometry and has numerous real-world applications. It allows us to solve problems involving right triangles and find missing side lengths, providing a valuable tool for mathematical and practical problem-solving.
Working with Different Units
When working with different units in mathematical problems, it is important to understand how to convert between them accurately. Units are used to measure various quantities such as length, weight, time, and temperature. Using the correct units and converting between them is crucial for obtaining accurate results in calculations.
Length: Length is measured in units such as inches, feet, meters, and miles. To convert between these units, conversion factors are used. For example, to convert inches to feet, divide the number of inches by 12. To convert meters to miles, divide the number of meters by 1609.34.
Weight: Weight is measured in units such as pounds, kilograms, and ounces. Conversion factors are also used to convert between these units. For example, to convert pounds to kilograms, multiply the number of pounds by 0.4536. To convert ounces to pounds, divide the number of ounces by 16.
Time: Time is measured in units such as seconds, minutes, hours, and days. Converting between these units can be done by using conversion factors. For example, to convert minutes to seconds, multiply the number of minutes by 60. To convert hours to days, divide the number of hours by 24.
Temperature: Temperature is measured in units such as degrees Celsius and degrees Fahrenheit. To convert between these units, specific formulas are used. For example, to convert degrees Celsius to degrees Fahrenheit, multiply the degrees Celsius by 9/5 and add 32. To convert degrees Fahrenheit to degrees Celsius, subtract 32 and multiply the result by 5/9.
When working with different units, it is always important to check the units of the given problem and ensure that the final answer is in the correct unit. Conversion factors and formulas should be used accurately to avoid any errors in calculations. Practice and familiarity with different units will help in resolving problems efficiently and obtaining accurate results.