
In Big Ideas Math Chapter 8, students are introduced to the concepts of equations and inequalities and learn how to solve them. This chapter is essential in developing students’ algebraic skills and problem-solving abilities. By understanding how to find solutions to equations and inequalities, students can apply these skills to real-life situations and mathematical problems.
Throughout this chapter, students will explore various methods and strategies for solving equations and inequalities. They will learn about the properties of equality and inequality, such as the addition and multiplication properties, and how to use them to isolate variables and find solutions. Students will also learn about graphing linear equations and inequalities on a coordinate plane and how to interpret these graphs.
The Big Ideas Math Chapter 8 answer key provides students with the opportunity to check their work and verify their solutions. It serves as a valuable resource for students to gauge their understanding of the material and identify any areas of weakness. By using the answer key, students can ensure that they are on the right track and make any necessary corrections to their work.
Overall, Big Ideas Math Chapter 8 focuses on equipping students with the necessary skills and strategies to solve equations and inequalities. It provides a solid foundation for future math courses and helps students develop critical thinking and problem-solving abilities. By mastering the concepts and techniques covered in this chapter, students will be well-prepared to tackle more complex mathematical problems and apply their knowledge in diverse situations.
Understanding the Big Ideas Math Curriculum

The Big Ideas Math curriculum is designed to provide a comprehensive and rigorous approach to mathematics education. It is based on the understanding that students learn best when they are actively engaged in the learning process. With a focus on real-world applications and problem-solving, the curriculum aims to develop students’ critical thinking and analytical skills.
One key aspect of the Big Ideas Math curriculum is its emphasis on conceptual understanding. Rather than relying solely on memorization and rote learning, the curriculum encourages students to develop a deep understanding of mathematical concepts and principles. This approach helps students make connections between different topics and apply their knowledge to solve complex problems.
The Big Ideas Math curriculum also incorporates a spiral progression model, where concepts are introduced and then revisited and reinforced over time. This allows students to develop a strong foundation in key mathematical topics and build upon their existing knowledge. Additionally, the curriculum provides ample opportunities for practice and review, ensuring that students have the necessary skills to succeed.
The curriculum is organized into chapters, each focusing on a specific mathematical topic. Within each chapter, students are introduced to new concepts and skills through engaging and interactive lessons. These lessons are designed to cater to a variety of learning styles and include a combination of hands-on activities, group work, and individual practice. Furthermore, the curriculum provides additional resources such as online tutorials and practice exercises for students to further enhance their understanding.
In conclusion, the Big Ideas Math curriculum offers a comprehensive and rigorous approach to mathematics education. By focusing on conceptual understanding, providing ample opportunities for practice, and incorporating a spiral progression model, the curriculum helps students develop a deep and lasting understanding of mathematical concepts and skills.
Chapter 8: Exploring Geometric Figures
In Chapter 8 of the Big Ideas Math curriculum, students will delve into the world of geometric figures. This chapter introduces various shapes and their properties, allowing students to deepen their understanding of geometry. By exploring different types of polygons, students will learn how to classify and differentiate between quadrilaterals, triangles, pentagons, and other polygons.
Throughout this chapter, students will also learn about the characteristics of each shape, such as the number of sides and angles, as well as how to calculate perimeter and area. They will have the opportunity to apply their knowledge by solving real-world problems and performing hands-on activities. By engaging in these activities, students will develop critical thinking and problem-solving skills, as well as gain a deeper appreciation for the importance of geometry in everyday life.
Key concepts covered in Chapter 8 include understanding the properties of quadrilaterals and triangles, identifying congruent and similar figures, and using formulas to find the perimeter and area of polygons. Students will also explore the concept of symmetry and how to identify lines of symmetry in various shapes.
By the end of Chapter 8, students will have a solid understanding of geometric figures and their properties. They will be able to recognize different shapes, classify them based on their attributes, and apply their knowledge to solve problems involving polygons. The skills and concepts learned in this chapter will serve as a foundation for further exploration of geometry in higher grade levels.
Section 2: Properties of Geometric Figures
In this section, we will explore the properties of various geometric figures, including polygons, circles, and triangles. Understanding these properties is essential when it comes to solving geometric problems and applying geometric principles in real-life situations.
Polygons: A polygon is a closed two-dimensional figure formed by straight lines. Some key properties of polygons include the number of sides, the sum of interior angles, and the types of angles and sides present. For example, a triangle has three sides, and the sum of its interior angles is always 180 degrees. A quadrilateral has four sides, and the opposite sides are parallel.
Circles: A circle is a geometric figure with all points equidistant from a central point. Some important properties of circles include the radius, diameter, circumference, and area. The radius is the distance from the center to any point on the circle, while the diameter is the distance across the circle through the center. The circumference is the distance around the circle, and the area is the space enclosed by the circle.
Triangles: A triangle is a polygon with three sides. Triangles have various properties, including the sum of interior angles, the lengths of sides, and the types of angles. The sum of interior angles in a triangle is always 180 degrees. Triangles can be classified based on their angles (as acute, obtuse, or right) or their sides (as equilateral, isosceles, or scalene).
By understanding the properties of these geometric figures, we can identify and analyze their characteristics, making it easier to solve problems involving them. These properties serve as the foundation for more advanced concepts in geometry and are crucial for applications in fields such as architecture, engineering, and computer science.
The Classification of Geometric Figures
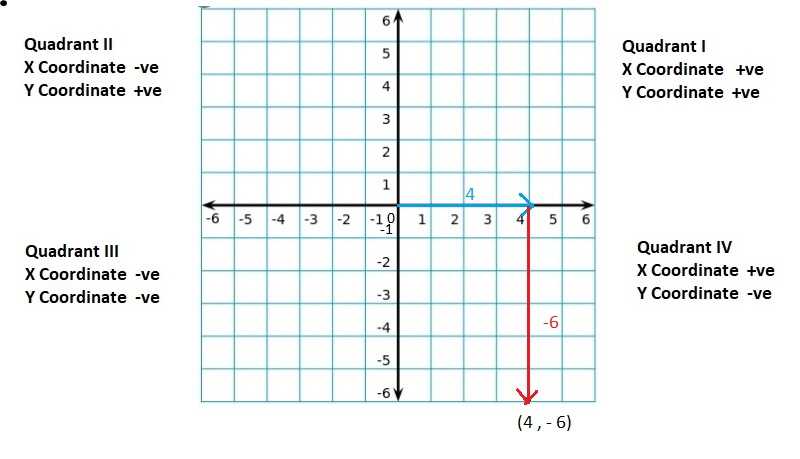
Section 3 of the Big Ideas Math chapter 8 focuses on the classification of geometric figures. Understanding the classification of different shapes is an important concept in geometry as it helps us identify and categorize various figures based on their properties and characteristics.
When classifying geometric figures, it is essential to consider their attributes such as the number of sides, angles, and symmetry. This section introduces students to different types of polygons, including triangles, quadrilaterals, pentagons, and hexagons, and teaches them how to identify and differentiate between these shapes based on their specific properties. Additionally, the section covers classification of lines, rays, and angles, providing students with the necessary tools to identify and classify these elements.
One of the key concepts covered in this section is the hierarchy of geometric figures. Students learn that geometric figures can be classified into subcategories based on their properties. For example, quadrilaterals can be further classified into rectangles, squares, rhombuses, and parallelograms based on their specific attributes. By understanding this hierarchy, students can better grasp the relationships between various figures and develop a deeper understanding of geometry.
This section also introduces students to the concept of congruence and similarity. Students learn that congruent figures have the same size and shape, while similar figures have the same shape but potentially different sizes. Understanding these concepts is essential for solving geometry problems and proving theorems.
In conclusion, Section 3 of the Big Ideas Math chapter 8 provides students with a comprehensive understanding of the classification of geometric figures. By learning to identify and classify different shapes based on their properties, students develop a strong foundation in geometry and can apply these concepts to solve more complex problems.
Section 4: Measuring Geometric Figures
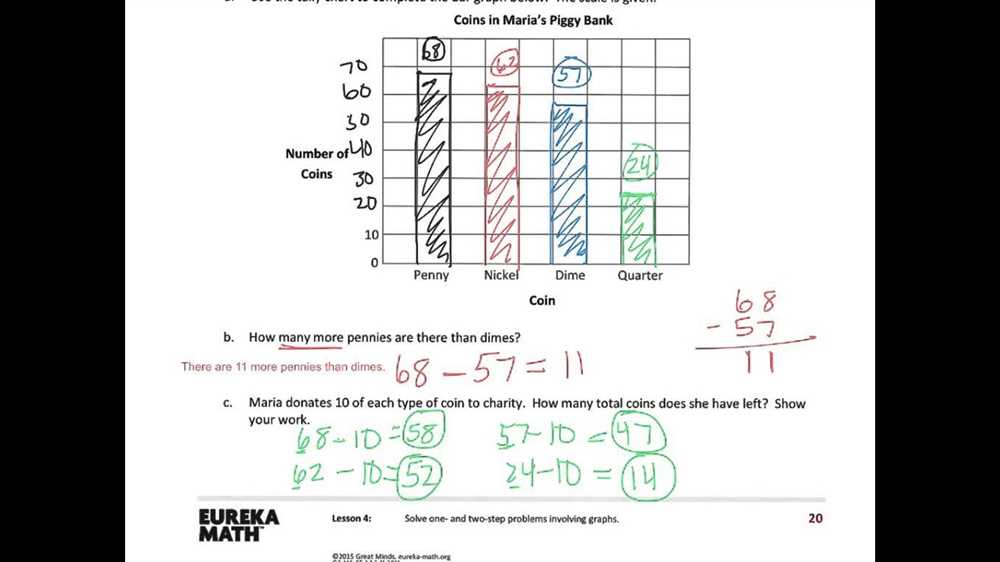
In Section 4 of Big Ideas Math Chapter 8, we will explore the concept of measuring geometric figures. It is essential to understand how to measure the length, area, and volume of various geometric shapes accurately. These measurements are crucial in real-world applications such as construction, architecture, and engineering. By learning how to measure geometric figures, we can solve practical problems and make informed decisions based on accurate measurements.
Measuring Length: When measuring the length of a geometric figure, it is important to use the appropriate unit of measurement. Common units of length include inches, feet, yards, centimeters, and meters. In this section, we will learn how to use rulers, tape measures, and other tools to measure the length of lines, segments, and curves. We will also explore different strategies for measuring irregular shapes, such as breaking them down into simpler components to get accurate measurements.
Measuring Area: The area of a geometric figure is the measure of its surface, expressed in square units. In this section, we will learn how to measure the area of two-dimensional shapes, such as rectangles, triangles, circles, and irregular shapes. We will explore different formulas and techniques to calculate the area accurately. Understanding the concept of area is vital in various fields, including landscaping, interior design, and manufacturing, where we need to determine the amount of material required to cover a given surface.
Measuring Volume: Volume is the measure of the space occupied by a three-dimensional geometric figure. In this section, we will learn how to measure the volume of common three-dimensional shapes, such as cubes, rectangular prisms, cylinders, and spheres. We will also explore strategies for measuring the volume of irregular shapes by breaking them down into simpler components. Understanding volume is crucial in fields like construction, architecture, and manufacturing, where we need to determine the capacity or amount of space occupied by an object.
By mastering the skill of measuring geometric figures, you will have a solid foundation for solving real-world problems and making accurate calculations. Throughout this section in Big Ideas Math Chapter 8, you will find practice exercises and examples that will help you develop your measuring skills and apply them to various scenarios. Embrace the challenge and enjoy the journey of exploring the world of measurement in geometry!
Section 5: Applying Geometric Figures
In this section, we will explore how to apply geometric figures to solve various mathematical problems. Geometry is the branch of mathematics that deals with shapes, sizes, properties, and relationships of objects. Geometric figures are the building blocks of geometry, and understanding their properties and characteristics can help us solve problems and make connections between different areas of mathematics.
One way to apply geometric figures is through the use of formulas. Formulas provide a concise way to express mathematical relationships, and they can be used to solve problems involving geometric figures. For example, the formula for the area of a rectangle is length multiplied by width. By knowing the values for length and width, we can calculate the area of a specific rectangle. Similarly, the formula for the circumference of a circle is 2 times pi times the radius. By knowing the radius of a circle, we can determine its circumference.
Geometric figures can also be used to solve real-world problems. For instance, understanding the properties of triangles can help us determine the height of a tall object, such as a flagpole or a tree. By using trigonometric ratios, we can calculate the height based on the length of its shadow and the angle of elevation. Additionally, geometric figures can be used in the fields of engineering and architecture to design and construct buildings, bridges, and other structures.
Overall, applying geometric figures allows us to solve problems, make connections between different areas of mathematics, and apply mathematics to the real world. By understanding the properties and characteristics of geometric figures, we can analyze and solve problems more effectively, and make connections between geometry and other areas of mathematics.
Section 6: Problem-Solving with Geometric Figures

In this section, we will explore various problem-solving techniques that involve geometric figures. These techniques will require us to apply our knowledge of geometric shapes, angles, and measurements in order to find solutions. By using logical reasoning and mathematical strategies, we can solve problems that involve finding missing measurements, determining the relationships between different shapes, and identifying patterns.
One problem-solving strategy that we will use is the process of elimination. This involves systematically ruling out impossible solutions in order to narrow down the possibilities. By using our understanding of geometric properties, such as the angles and side lengths of shapes, we can eliminate options that do not fit the given criteria. This approach allows us to focus on the most viable solutions and increase our chances of finding the correct answer.
Example Problem:
Suppose we are given a triangle ABC, and we know that angle A measures 60 degrees and angle B measures 90 degrees. We are asked to find the measure of angle C. To solve this problem, we can use the fact that the sum of the angles in a triangle is always 180 degrees. Since we know the measures of angles A and B, we can subtract their sum from 180 to find the measure of angle C:
- Angle C = 180 – (60 + 90)
- Angle C = 30 degrees
Therefore, the measure of angle C in triangle ABC is 30 degrees.
In addition to the process of elimination, we can also use other problem-solving techniques such as creating diagrams, using algebraic equations, and applying geometric theorems. These approaches help us break down complex problems into smaller, more manageable steps. By engaging in critical thinking and applying our knowledge of geometric concepts, we can successfully solve problems involving geometric figures.