Geometry is a branch of mathematics that deals with the properties and relationships of shapes, sizes, and dimensions. Its study is crucial in understanding the world around us, from the simplest objects to complex structures. One way to assess our understanding of geometric concepts is through tests, and one such test is the Ch 10 geometry test.
The Ch 10 geometry test is designed to evaluate students’ knowledge and skills in specific topics covered in Chapter 10 of their geometry textbook. This chapter typically focuses on advanced concepts such as angles, circles, and transformations. It is an opportunity for students to demonstrate their understanding of these topics and apply them to real-world scenarios.
Preparing for the Ch 10 geometry test requires thorough review of the chapter material, practice solving problems, and familiarization with geometric formulas and theorems. Students are encouraged to engage in active learning, such as participating in class discussions, seeking clarification from their teachers, and working on practice exercises.
The Ch 10 geometry test serves as an important assessment tool for both students and teachers. It allows students to gauge their understanding of the material and identify areas where they may need additional study and practice. For teachers, the test provides valuable information about their students’ learning progress and helps guide their instruction to better meet the needs of individual learners.
Overview of Ch 10 geometry
In Chapter 10 of the geometry textbook, students will dive deeper into the world of geometric shapes, angles, and measurements. This chapter builds upon the foundational knowledge from previous chapters and introduces new concepts and theorems that will expand students’ understanding of geometry.
Key topics:
- Triangles: Students will explore different types of triangles, such as scalene, isosceles, and equilateral triangles. They will learn about the properties of triangles, including the sum of interior angles and the types of angles within a triangle.
- Quadrilaterals: This section focuses on quadrilaterals, including squares, rectangles, parallelograms, and trapezoids. Students will learn about the properties and characteristics of each type of quadrilateral.
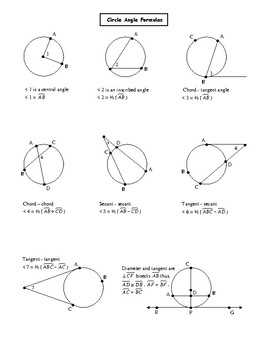
- Circles: In this chapter, students will study circles and their properties, including the relationships between radii, diameters, and chords. They will also explore central angles and inscribed angles within circles.
- Geometric proofs: Throughout this chapter, students will develop and practice their skills in geometric proofs. They will apply the theorems and properties they have learned to prove various geometric statements.
- Coordinate geometry: The chapter also introduces the concept of coordinate geometry, where students will learn how to plot points on a coordinate plane and find the distance and midpoint between two points.
This chapter provides a comprehensive overview of important geometric concepts and their applications. By mastering the material in Chapter 10, students will be well-prepared for more advanced topics in geometry and other areas of mathematics.
Understanding the concepts of Ch 10 geometry
In Chapter 10 of our geometry textbook, we delve into more advanced concepts that build upon the fundamental principles we have learned so far. This chapter focuses on topics such as geometric constructions, congruence, and proofs. By understanding the concepts covered in this chapter, we will be equipped with the tools to tackle more complex geometric problems and gain a deeper understanding of the subject.
One of the key concepts covered in Chapter 10 is geometric constructions. Geometric constructions involve drawing various figures using only a compass and straightedge. By following specific steps and guidelines, we can construct various geometric shapes such as triangles, quadrilaterals, and regular polygons. Understanding these constructions allows us to visualize and manipulate geometric figures, which can aid us in solving problems and proving theorems.
Another important concept in Chapter 10 is congruence. Congruence refers to the idea that two figures are identical in size and shape. We learn about different criteria for proving congruence, such as side-angle-side (SAS), side-side-side (SSS), and angle-side-angle (ASA). By recognizing and applying these criteria, we can determine if two figures are congruent and use that information to solve problems involving congruent triangles and other geometric shapes.
The final major concept in Chapter 10 is proofs. Proofs are a vital part of geometry as they allow us to logically demonstrate the validity of geometric statements. We explore different proof techniques, such as direct proofs, indirect proofs, and proof by contradiction. Understanding how to construct and articulate proofs not only strengthens our ability to reason mathematically but also helps us develop critical thinking skills that can be applied in a variety of contexts.
By mastering the concepts covered in Chapter 10, we will be equipped with the necessary tools and knowledge to tackle more challenging geometry concepts in future chapters. The understanding of geometric constructions, congruence, and proofs will not only enhance our problem-solving abilities but also provide a solid foundation for further exploration into geometry and related disciplines.
Important theorems and postulates in Ch 10 geometry
Geometry is a branch of mathematics that deals with the study of shapes, sizes, and properties of figures and spaces. In Chapter 10 of geometry, several important theorems and postulates are introduced to help analyze and understand the properties of triangles.
One of the key theorems in Chapter 10 is the Pythagorean theorem. This theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is widely used in various geometric and real-world applications, such as calculating distances, constructing right angles, and solving problems involving right triangles.
Another significant concept in Chapter 10 is the Triangle Proportionality Theorem, also known as the Side-Splitter Theorem. This theorem states that if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. It provides a useful tool for solving problems involving similar triangles and proportional relationships within triangles.
Additionally, the Angle Bisector Theorem is introduced in Chapter 10. This theorem states that an angle bisector divides the opposite side of a triangle into segments that are proportional to the lengths of the adjacent sides. It is often used to find unknown side lengths or to prove congruence or similarity of triangles.
These theorems and postulates play a crucial role in the study of Chapter 10 geometry. They provide the foundation for solving various geometric problems, analyzing relationships between sides and angles of triangles, and exploring the properties of different types of triangles. Understanding and applying these theorems is essential for mastering the concepts and techniques of geometry.
Some other important theorems and postulates in Ch 10 geometry are:
- The Exterior Angle Theorem
- The Triangle Inequality Theorem
- The SAS Congruence Postulate
- The ASA Congruence Theorem
- The SSS Congruence Theorem
These theorems and postulates provide additional tools for analyzing triangles, proving congruence or similarity, and solving various geometric problems.
Key definitions in Ch 10 geometry
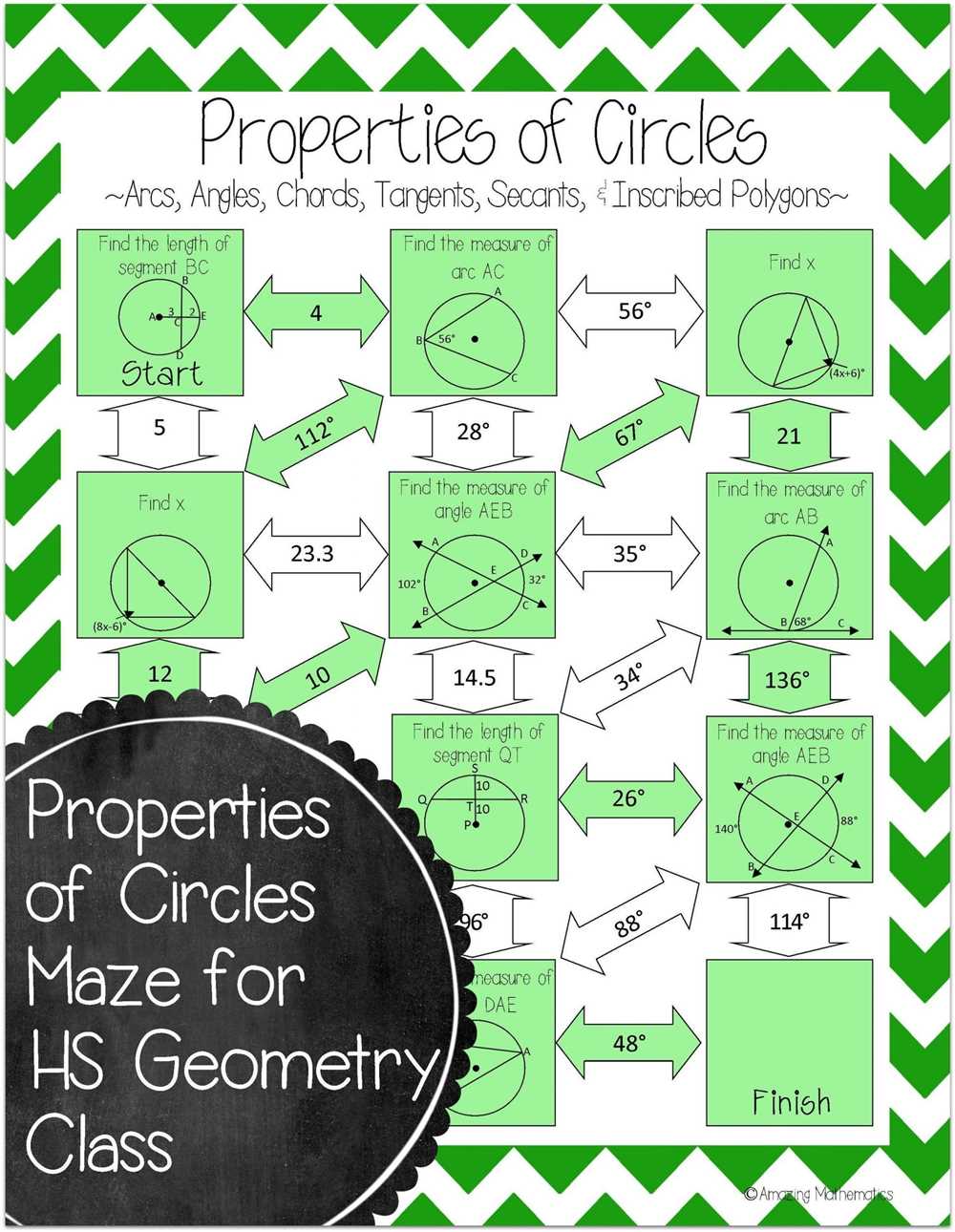
In Chapter 10 of geometry, there are several key definitions that are important to understand. These definitions are essential in order to grasp the concepts and principles of geometry. Here are some of the key definitions:
1. Angle:
An angle is a figure formed by two rays that share a common endpoint, called the vertex. The rays are called the sides of the angle. Angles can be measured in degrees or radians and are classified based on their measurement.
2. Triangle:
A triangle is a polygon with three sides, three angles, and three vertices. Triangles can be classified based on their side lengths and angle measurements, such as equilateral, isosceles, scalene, acute, right, or obtuse.
3. Quadrilateral:
A quadrilateral is a polygon with four sides, four angles, and four vertices. Quadrilaterals can be classified based on the lengths of their sides and properties of their angles, such as rectangle, rhombus, square, parallelogram, trapezoid, or kite.
4. Circle:
A circle is a two-dimensional figure that is defined as the set of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is called the radius, and the distance across the circle through the center is called the diameter.
5. Polyhedron:

A polyhedron is a three-dimensional figure with flat faces and straight edges. Examples of polyhedra include prisms, pyramids, cubes, and dodecahedrons.
These are just a few of the key definitions in Chapter 10 of geometry. Understanding these definitions is crucial for solving geometric problems and applying geometric principles in various real-world scenarios.
Reviewing previous chapters
In the previous chapters, we covered a variety of important topics in geometry. We started by exploring the basic concepts of lines, angles, and polygons. We learned about different types of lines, such as parallel and perpendicular lines, and how to identify and measure angles. We also studied the properties of polygons, including triangles, quadrilaterals, and circles.
Next, we delved into the world of triangles and their properties. We learned about the different types of triangles, including equilateral, isosceles, and scalene triangles, and how to calculate their areas and perimeters. We also explored the Pythagorean theorem and its applications in solving problems involving right triangles.
Afterwards, we moved on to quadrilaterals and circles. We discovered the properties of various types of quadrilaterals, such as rectangles, squares, parallelograms, and trapezoids. We learned how to calculate the area and perimeter of these shapes. Additionally, we delved into the properties of circles, including the radius, diameter, circumference, and area formulas.
In the later chapters, we explored transformations and congruence. We studied translations, reflections, rotations, and dilations, and how they affect the shape and position of figures. We also learned about symmetry and tessellations. Lastly, we discussed congruent figures and how to determine if two figures are congruent using various criteria and postulates.
Overall, reviewing the previous chapters has provided us with a solid foundation in geometry, equipping us with the necessary knowledge and skills to tackle more complex problems in the upcoming chapters.
Practicing Geometry Problems
Geometry is a branch of mathematics that deals with the properties and relationships of shapes and figures. It involves applying various formulas and theorems to solve problems related to angles, lines, triangles, circles, and other geometric concepts. To become proficient in geometry, it is essential to practice solving a variety of problems.
Practicing geometry problems helps to enhance problem-solving skills and develop a deeper understanding of geometric principles. By actively engaging in problem-solving, students can improve their ability to visualize and analyze geometric figures, which is crucial for applying geometric concepts in real-life situations. Regular practice also helps to reinforce memorization of formulas and theorems, making it easier to recall them when needed.
To effectively practice geometry problems, it is recommended to start with basic concepts and gradually progress to more complex ones. This allows students to build a strong foundation and gain confidence in solving various types of geometric problems. It is also helpful to identify common problem-solving strategies, such as drawing accurate diagrams, utilizing symmetry, and applying logical reasoning, to approach different types of geometry problems.
As you practice geometry problems, it is important to pay attention to the details and be meticulous in your calculations. Carefully read and analyze each problem to understand the given information and identify the required solution. Break down complex problems into smaller, manageable steps and use your knowledge of geometric principles to guide your approach.
Practicing geometry problems regularly not only helps to improve your problem-solving skills but also prepares you for geometry tests and exams. By being familiar with different types of problems and having a clear understanding of geometric concepts, you will be better equipped to tackle challenging questions and achieve success in your geometry studies. So, keep practicing and exploring the fascinating world of geometry!
Managing Your Time During the Test
In order to succeed on your geometry test, it is crucial to manage your time effectively. Time management plays a significant role in ensuring that you have enough time to complete all the questions and review your answers.
Plan your time: Before starting the test, take a few minutes to read through all the questions and allocate time for each one based on its difficulty. This will help you stay on track and avoid spending too much time on a challenging question.
Use a time tracker: Consider using a stopwatch or a timer to keep track of how much time you spend on each question. This will help you stay focused and ensure that you are not spending too much time on one question at the expense of others.
Answer the easy questions first: Start with the questions that you find relatively easy and quickly move through them. This will boost your confidence and save you time for the more challenging questions later on.
Manage your breaks wisely: If the test allows for breaks, use them strategically. Take short breaks to stretch, relax, and clear your mind. However, be mindful of not taking too many breaks, as this can eat into your testing time.
Stay calm and focused: It’s natural to feel stressed during a test, but try to keep calm and focused. If you encounter a difficult question, take a deep breath, relax, and try your best. Don’t let one question consume all your time and energy.
Review your answers: Once you have finished answering all the questions, use the remaining time to review your answers. Check for any mistakes or errors, and make any necessary changes. This step is essential for catching any careless mistakes you may have made during the test.
Don’t rush: While it is important to manage your time, do not rush through the test. Take your time, read each question carefully, and ensure that you understand what is being asked. Rushing can lead to careless errors and misunderstandings.
By implementing these time-management strategies, you will be able to effectively allocate your time, stay focused, and maximize your chances of success on your geometry test.