
Understanding functions and graphs is a crucial part of learning mathematics. In Chapter 1, students are introduced to the basic concepts of functions, such as domain and range, as well as different types of functions, like linear and quadratic. They also learn how to graph these functions and analyze their properties.
When working through the problems in Chapter 1, students may encounter various challenges and have questions about their answers. This article aims to provide answers to the exercises and problems in Chapter 1, helping students clarify their understanding and reinforce their knowledge of functions and graphs.
By addressing common misconceptions, explaining important concepts, and providing step-by-step solutions, this article will serve as a valuable resource for students who want to review or seek further clarification on the topics covered in Chapter 1. Whether you are a student looking for answers or a teacher seeking additional resources for your students, this article will help consolidate your understanding of functions and graphs.
Chapter 1 Functions and Graphs Answers

In Chapter 1, we have explored the concept of functions and how they are represented graphically. In this section, we provide answers to the exercises and questions from this chapter to help you better understand the material.
1. Evaluating Functions
In the exercises that require evaluating functions, we utilize the given input values and substitute them into the function to obtain the corresponding output values. These output values help us understand how the function behaves for different inputs.
2. Graphing Functions
When graphing functions, we plot points on a coordinate plane based on the input and output values. By connecting these points, we can visualize the shape of the function’s graph and determine its behavior. It is important to pay attention to key features such as intercepts, asymptotes, and the overall trend of the graph.
3. Domain and Range
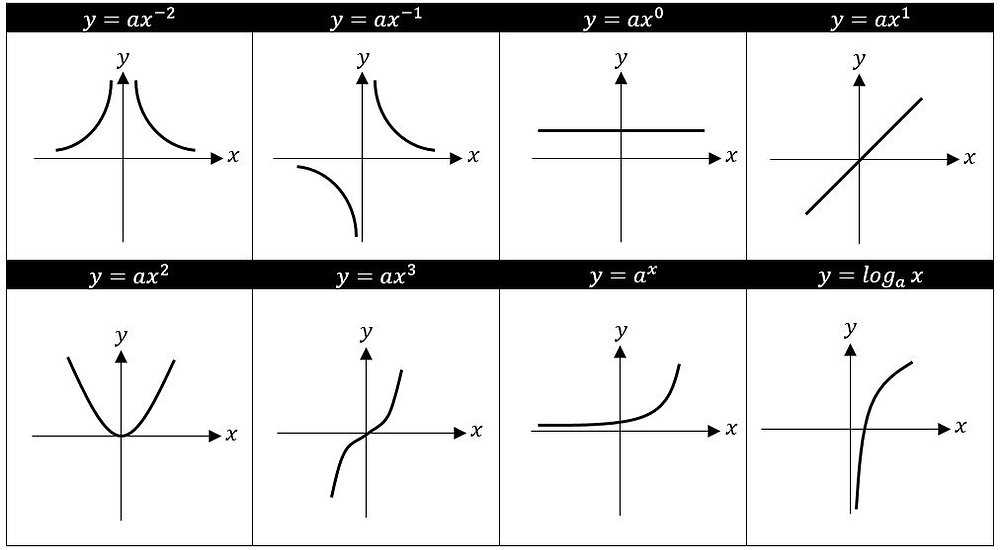
The domain of a function refers to the set of possible input values for which the function is defined. The range, on the other hand, represents the set of output values that the function can produce. To determine the domain and range of a function, we look for any restrictions or limitations on the input and output values based on the function’s definition or graph.
4. Piecewise Functions
Piecewise functions are functions that are defined by different formulas or rules for different intervals or subsets of the domain. To work with piecewise functions, we evaluate the function separately for each piece based on the given x-values or intervals. It is important to carefully consider the conditions and corresponding formulas for each interval to obtain accurate results.
5. Operations with Functions
When performing operations with functions, we combine or manipulate the given functions based on the specific operation being performed. Common operations include addition, subtraction, multiplication, division, and composition of functions. The answers to these exercises involve applying the appropriate operations and simplifying the resulting expressions.
Understanding Functions and Graphs
A function is a mathematical concept that relates an input value to an output value. It can be thought of as a rule or a set of instructions that transforms the input into the corresponding output. Functions can be represented graphically using a coordinate system, where the input values are plotted on the x-axis and the output values on the y-axis. This graphical representation of a function is called its graph.
In order to understand functions and graphs, it is important to grasp the concept of domain and range. The domain of a function refers to all possible input values, while the range represents all possible output values. The domain and range of a function can be determined by examining its graph.
Key phrases:
- Function
- Input value
- Output value
- Rule
- Graph
- Coordinate system
- Domain
- Range
Functions can have various forms, such as linear, quadratic, exponential, and trigonometric. Each type of function has a distinct graph and specific characteristics. For example, linear functions have graphs that are straight lines, while quadratic functions have graphs that are parabolas.
Understanding functions and graphs is essential in various fields, including mathematics, physics, engineering, and economics. Functions and graphs allow us to model and analyze real-world phenomena, make predictions, and solve problems. They provide a visual representation of the relationship between different variables and help us understand the behavior and patterns in data.
Solving Linear Equations
Linear equations are mathematical equations that involve only one variable, typically represented by the letter “x”. These equations can be solved by isolating the variable on one side of the equation and simplifying the other side. Solving linear equations is an important skill in algebra, as it allows us to find the value or values of the variable that make the equation true.
One method for solving linear equations is to use inverse operations. This involves performing the opposite operation to both sides of the equation in order to isolate the variable. For example, if the equation is 2x + 5 = 15, we can subtract 5 from both sides to get 2x = 10. Then, we divide both sides by 2 to find that x = 5. This means that when x is equal to 5, the equation is true.
Another approach to solving linear equations is to use the concept of balancing. We can think of the equation as a scale, with the variable on one side and the constant terms on the other side. The goal is to make both sides of the equation equal by performing the same operation on both sides. For example, if the equation is 3x – 7 = 8, we can add 7 to both sides to get 3x = 15. Then, dividing both sides by 3, we find that x = 5.
- Inverse operations and balancing are two common methods for solving linear equations.
- It is important to perform the same operation on both sides of the equation to maintain equality.
- The solution to a linear equation is the value or values of the variable that make the equation true.
Understanding how to solve linear equations is essential in algebra and lays the foundation for solving more complex equations and systems of equations. By practicing these methods and developing a strong understanding of the underlying concepts, students can become proficient in solving linear equations and apply this skill to various real-world situations.
Graphing Equations
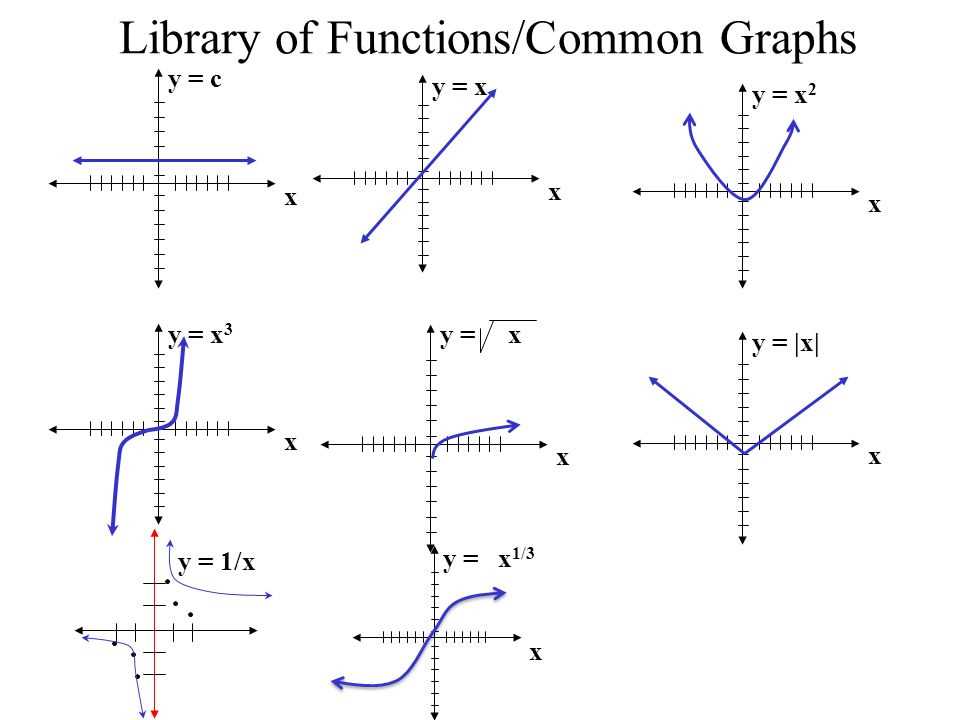
Graphing equations is an essential skill in mathematics and is commonly used to visualize relationships between variables. By graphing an equation, we can understand and interpret its behavior, identify key features, and make predictions about its solutions.
To graph an equation, we first need to understand its basic form. Most equations can be written in the form y = f(x), where y represents the dependent variable and x represents the independent variable. The equation describes how the value of y changes as x varies.
One way to graph an equation is to create a table of x and y values. We choose a range of x values, plug them into the equation to calculate the corresponding y values, and then plot the points on a coordinate plane. By connecting these points, we can sketch the graph of the equation.
In some cases, the equation may be linear, meaning it represents a straight line. Linear equations can be graphed by identifying the slope (rate of change) and the y-intercept (where the line crosses the y-axis). The slope determines the steepness of the line, while the y-intercept gives us a starting point.
Other equations may represent curves or other complex shapes. For these equations, we may need to use specific techniques and tools, such as transformations, symmetry, or calculus, to accurately graph the equation.
Graphing equations allows us to visualize mathematical concepts, analyze data, and solve real-world problems. It is a powerful tool that helps us understand the relationships and patterns that exist in the world around us.
Finding the Slope of a Line
Slope is a measure of how steep a line is. It represents the ratio of the vertical change to the horizontal change between two points on a line. To find the slope of a line, you need to determine the change in y-coordinates (vertical change) and the change in x-coordinates (horizontal change) between two points on the line. The formula for finding the slope is:
Slope = (change in y-coordinates) / (change in x-coordinates)
The slope can be represented by a numerical value or as a fraction. A positive slope indicates that the line is increasing from left to right, while a negative slope indicates that the line is decreasing. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
When given two points on a line, you can use the formula to calculate the slope. First, identify the coordinates of the two points: (x₁, y₁) and (x₂, y₂). Then, subtract the y-coordinates and the x-coordinates to find the changes in y and x, respectively. Finally, divide the change in y by the change in x to find the slope.
You can also determine the slope by looking at the equation of a line in slope-intercept form, y = mx + b. In this form, the coefficient of x, m, represents the slope of the line. The y-intercept, b, represents the point where the line crosses the y-axis.
In summary, the slope of a line measures its steepness and can be found by calculating the ratio of the change in y-coordinates to the change in x-coordinates between two points. It can also be determined from the equation of the line in slope-intercept form. Understanding how to find the slope is crucial in analyzing and interpreting graphs and equations.
Understanding Exponential Functions
An exponential function is a mathematical function of the form f(x) = a * b^x, where a and b are constants and x represents the input variable. Exponential functions are characterized by a constant base raised to a variable exponent.
Exponential functions have unique properties that distinguish them from other types of functions. One key property is exponential growth or decay, which is determined by the value of the base, b. If b is greater than 1, the function exhibits exponential growth, while if b is between 0 and 1, the function represents exponential decay.
Exponential functions are commonly used to model natural phenomena such as population growth, radioactive decay, and compound interest. They also appear in various fields of science and engineering, including physics, biology, and economics.
Understanding exponential functions involves analyzing their key characteristics, such as the asymptotic behavior (approaching but never reaching a certain value), rate of growth or decay, and the y-intercept (the value of f(x) when x is 0). By studying these properties, we can make predictions about the behavior of exponential functions and solve problems involving them.
In summary, exponential functions are powerful mathematical tools that can describe exponential growth or decay. By understanding their properties and analyzing their behavior, we can gain insights into real-world phenomena and make informed decisions in various fields.
Solving Quadratic Equations
Quadratic equations are equations that contain a squared term, such as x^2, as well as a linear term and a constant term. These equations are widely used in various fields of mathematics and physics, as they describe many real-life situations and phenomena. Solving quadratic equations is an essential skill in algebra, and it involves finding the values of x that make the equation true.
There are several methods to solve quadratic equations, depending on the form of the equation. One common method is factoring, where the quadratic equation is written as a product of two binomials. This method requires recognizing patterns and using algebraic manipulations to simplify the equation. Factoring is often the fastest method if the equation can be easily factored.
If factoring is not possible, the quadratic formula can be used to find the solutions. The quadratic formula states that for an equation of the form ax^2 + bx + c = 0, the solutions are given by x = (-b ± √(b^2 – 4ac))/(2a). This formula can be derived by completing the square, and it provides a straightforward way to find the solutions of any quadratic equation.
Another method for solving quadratic equations is completing the square. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily solved. Completing the square is particularly useful when dealing with quadratic equations that do not factor easily or when the quadratic formula is not preferred.
Overall, solving quadratic equations requires a combination of algebraic skills and problem-solving strategies. By understanding the different methods and when to use them, you can confidently solve quadratic equations and apply them to various mathematical and real-life situations.
Graphing Quadratic Equations
A quadratic equation is a polynomial equation of the form y = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic equation is a curve called a parabola.
To graph a quadratic equation, we need to find the y-intercept and the x-intercepts, if any. The y-intercept is the point where the curve intersects the y-axis, and it can be found by substituting x = 0 into the equation. The x-intercepts, also known as the roots or zeros of the equation, are the points where the curve intersects the x-axis. They can be found by solving the equation ax^2 + bx + c = 0 using factoring, completing the square, or the quadratic formula.
To further analyze the graph of a quadratic equation, we can determine its axis of symmetry and vertex. The axis of symmetry is a vertical line that divides the parabola into two symmetrical halves. It can be found using the formula x = -b/2a. The vertex of the parabola is the point where the axis of symmetry intersects the curve, and it can be determined by substituting the x-coordinate of the axis of symmetry into the equation.
By plotting the y-intercept, x-intercepts, axis of symmetry, and vertex, we can then draw a smooth curve through these points to graph the quadratic equation. It is also helpful to determine the direction of the parabola, which depends on the sign of the coefficient a. If a is positive, the parabola opens upward, and if a is negative, the parabola opens downward.
Understanding how to graph quadratic equations is essential in various areas of mathematics and science, such as physics, engineering, and optimization problems. Graphing quadratic equations allows us to visualize the behavior and characteristics of these equations, making it easier to analyze and solve related problems.