Welcome to the answer key for Chapter 2 of the motion in one dimension. In this chapter, we will be exploring the concept of motion in a single dimension or straight line. From understanding the basic definitions and principles to solving various problems and scenarios, this chapter will provide you with a solid foundation in the topic.
To fully understand and grasp the concepts, it is important to have access to the answer key. This will allow you to check your solutions and verify your understanding of the material. The answer key will serve as a valuable resource to guide you through the chapter and ensure you are on the right track.
Throughout this answer key, you will find detailed explanations, step-by-step solutions, and additional tips and insights to help you fully comprehend the concepts presented in the chapter. It is crucial to go through each question and its corresponding answer in order to reinforce your understanding and improve your problem-solving skills.
Whether you are a student preparing for an upcoming exam or a curious individual seeking a deeper understanding of motion in one dimension, this answer key will serve as an invaluable tool. So let’s dive into Chapter 2 and explore the exciting world of motion in a single dimension!
Chapter 2 Motion in One Dimension Answer Key
Chapter 2 of the physics textbook delves into the topic of motion in one dimension. It provides an in-depth understanding of how objects move in a straight line and how to analyze the various factors that affect their motion. To help students assess their understanding and progress, an answer key is provided at the end of the chapter.
The answer key for Chapter 2 covers a range of topics, including concepts such as displacement, velocity, and acceleration. It provides step-by-step solutions to the practice problems and exercises presented throughout the chapter, allowing students to check their work and ensure they have a grasp of the material. The answer key also includes explanations and explanations for each solution, giving students an opportunity to learn from any mistakes they may have made.
In addition to the numerical problems, the answer key also includes conceptual questions that require a deeper understanding of the principles discussed in the chapter. These questions may prompt students to think critically and apply their knowledge to real-world scenarios. The answer key provides clear and concise explanations for each concept, enabling students to strengthen their conceptual understanding of motion in one dimension.
The answer key serves as a valuable resource for both students and educators. Students can use it to check their progress, identify areas of weakness, and seek additional clarification on specific topics. Educators can utilize the answer key as a reference to guide their instruction and ensure they are accurately assessing their students’ comprehension.
In conclusion, the Chapter 2 Motion in One Dimension Answer Key is an essential tool for students studying the principles of motion in one dimension. It provides comprehensive solutions and explanations for numerical and conceptual problems, enabling students to solidify their understanding and apply their knowledge to various scenarios.
What is One-Dimensional Motion?
One-dimensional motion refers to the movement of an object along a single straight line. It involves the measurement of distance and time, as well as the calculation of speed and velocity. In this type of motion, there is no change in direction, and the object moves only along the line without any lateral or vertical movement.
In one-dimensional motion, the object’s position is measured relative to a reference point, usually referred to as the origin. The direction of motion is determined by using positive and negative numbers, with positive values indicating motion in one direction and negative values indicating motion in the opposite direction.
In order to describe and analyze one-dimensional motion, various concepts and equations are used. These include displacement, which is the change in position of an object, and velocity, which is the rate at which an object’s position changes with respect to time. Additionally, acceleration, which is the rate at which an object’s velocity changes with time, is also considered in the study of one-dimensional motion.
One-dimensional motion can be further categorized into different types, such as uniform motion and non-uniform motion. Uniform motion refers to when an object moves with constant velocity, while non-uniform motion occurs when the velocity of the object changes over time. Understanding and analyzing one-dimensional motion is crucial in various fields, including physics, engineering, and kinematics.
Equations of One-Dimensional Motion
When studying the motion of objects in one-dimensional space, it is important to understand the equations that describe this motion. These equations relate the position, velocity, acceleration, and time of an object, and can be used to analyze and predict its behavior.
The main equation that describes one-dimensional motion is the displacement equation. It states that the displacement of an object is equal to its initial velocity multiplied by time, plus half the acceleration multiplied by the square of time. This equation can be written as:
Δx = v0t + 1/2at2
where Δx represents the displacement, v0 represents the initial velocity, t represents time, and a represents acceleration. This equation is derived from the definition of acceleration, which is the rate at which the velocity of an object changes with time.
In addition to the displacement equation, there are other equations that can be derived from it. For example, the velocity equation states that the final velocity of an object is equal to its initial velocity plus the product of acceleration and time. It can be written as:
v = v0 + at
This equation allows us to calculate the velocity of an object at any given time, given its initial velocity and acceleration. Similarly, the acceleration equation states that the acceleration of an object is equal to the change in velocity divided by the change in time. It can be written as:
a = Δv/Δt
These equations of one-dimensional motion are fundamental to understanding and analyzing the behavior of objects in motion. They can be used to solve various problems related to motion, such as determining the initial velocity or acceleration of an object, or predicting its future position or velocity.
Displacement and Velocity

Displacement is a crucial concept in the study of motion in one dimension. It refers to the change in an object’s position from its initial location to its final location. Displacement is a vector quantity, meaning it has both magnitude and direction. It can be positive if the object moves in one direction, negative if it moves in the opposite direction, or zero if it returns to its initial position.
Velocity, on the other hand, is the rate at which an object changes its position. It is a vector quantity that combines the concepts of speed (magnitude) and direction. Velocity can be calculated by dividing the displacement of an object by the time taken to cover that distance. It is important to note that velocity is not the same as speed, as speed only refers to the magnitude of the motion without considering direction.
- Displacement is the change in an object’s position, while velocity is the rate of change of that position.
- Displacement is a vector quantity, while velocity is also a vector quantity that includes both magnitude and direction.
- Displacement can be positive, negative, or zero, depending on the direction of the motion.
- Velocity is calculated by dividing displacement by time, while speed is calculated by dividing distance by time.
- It is important to consider both displacement and velocity when analyzing the motion of an object in one dimension.
Overall, understanding displacement and velocity is key to comprehending the motion of an object in one dimension. These concepts allow us to describe and quantify the changes in an object’s position over time, helping us to better understand the physical world around us.
Acceleration and Uniformly Accelerated Motion

The concept of acceleration plays a crucial role in understanding the motion of objects in one dimension. Acceleration is defined as the rate at which an object changes its velocity. It is a vector quantity, meaning it has both magnitude and direction. When an object’s velocity increases, it is said to have positive acceleration, while a decrease in velocity results in negative acceleration, also known as deceleration.
In uniformly accelerated motion, the acceleration remains constant throughout the motion. This means that the object’s velocity changes by the same amount in equal intervals of time. One of the key equations for uniformly accelerated motion is the equation of motion, which relates the final velocity (v), initial velocity (u), acceleration (a), and displacement (s): v^2 = u^2 + 2as. This equation allows us to calculate any of the variables if we know the values for the others.
To illustrate uniformly accelerated motion, let’s consider the example of a car starting from rest and accelerating at a constant rate. As time progresses, the car’s velocity will increase linearly, while its displacement will increase quadratically. This relationship between time and displacement is described by the equation s = ut + 0.5at^2, where s is the displacement, u is the initial velocity, a is the acceleration, and t is the time elapsed.
In summary, acceleration is the rate at which an object changes its velocity, and in uniformly accelerated motion, the acceleration remains constant. This allows us to use equations to analyze the motion of objects in one dimension and calculate various parameters such as velocity, displacement, and time. Understanding acceleration and uniformly accelerated motion is fundamental to studying the behavior of objects in motion.
Applications of One-Dimensional Motion
One-dimensional motion, also known as linear motion, refers to the movement of an object along a straight line. It is a fundamental concept in physics, and its applications can be found in various fields.
Transportation: One-dimensional motion plays a crucial role in transportation systems. Whether it’s a car, a train, or a plane, understanding the principles of linear motion helps engineers design vehicles that can efficiently move from one point to another. By analyzing the motion of these vehicles, engineers can determine factors such as speed, acceleration, and braking distance, which contribute to overall safety and efficiency of transportation systems.
Sports: Many sports involve one-dimensional motion. For example, in track and field events, such as the 100-meter sprint and long jump, athletes aim to achieve maximum speed and distance in a straight line. By analyzing the motion of athletes, coaches can identify areas for improvement and develop training strategies to enhance their performance. Similarly, in sports like baseball, the trajectory of a ball thrown or hit can be analyzed using the principles of one-dimensional motion, providing insights into the game strategies and tactics.
Mechanical Engineering: The principles of one-dimensional motion are fundamental to mechanical engineering. Engineers use concepts such as displacement, velocity, and acceleration to design machines and mechanisms that can perform tasks in a controlled and efficient manner. For example, in robotics, understanding the motion of robotic arms and manipulators is essential for programming and controlling their movements. By applying the laws of one-dimensional motion, engineers can optimize the design and performance of mechanical systems.
Astronomy: Even in the vastness of space, the concept of one-dimensional motion is applicable. Astronomers study the motion of celestial objects, such as planets, stars, and galaxies, using the principles of linear motion. By analyzing the positions, velocities, and accelerations of these objects, astronomers can make predictions about their future trajectories and understand the behavior of the universe on a grand scale.
Conclusion: One-dimensional motion is a fundamental concept that finds applications in various fields, including transportation, sports, mechanical engineering, and astronomy. Understanding and analyzing the motion of objects along a straight line enables us to design better vehicles, improve sports performance, optimize mechanical systems, and explore the mysteries of the universe.
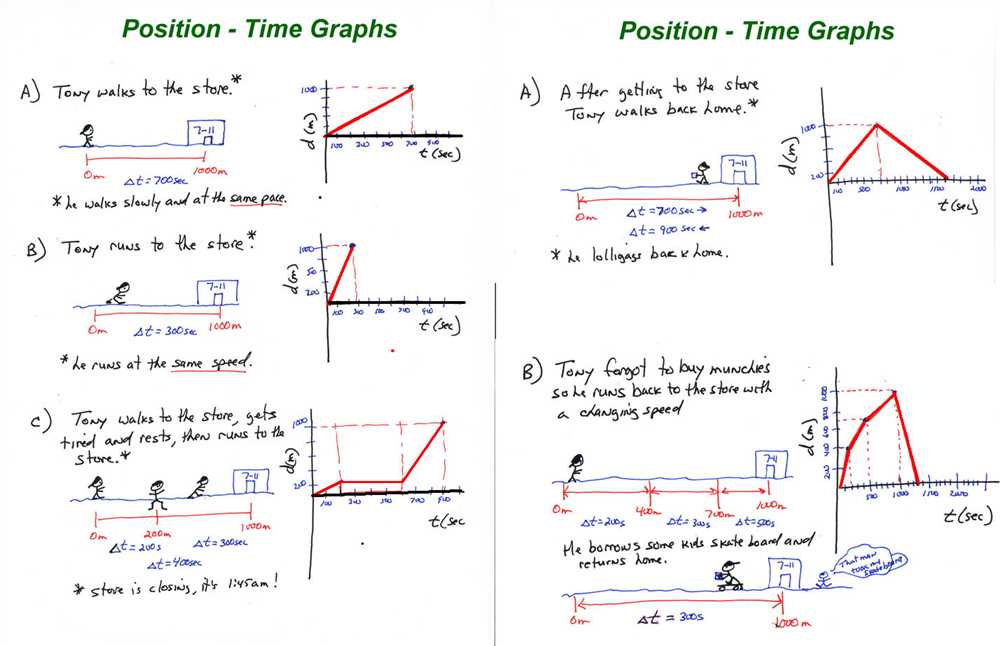
Graphical Representation of One-Dimensional Motion

In the study of one-dimensional motion, it is often useful to represent the motion graphically. Graphs can provide a visual representation of the relationship between different variables and can help in analyzing and understanding the motion. One commonly used graph is the position-time graph, which shows the position of an object as a function of time.
A position-time graph consists of two axes – the horizontal axis represents time, while the vertical axis represents position. The graph shows how the position of the object changes over time. The slope of the graph indicates the object’s velocity – a steeper slope represents a higher velocity, while a flatter slope represents a lower velocity.
Another type of graph used in one-dimensional motion is the velocity-time graph. This graph shows how the velocity of an object changes over time. The slope of the velocity-time graph represents the object’s acceleration – a positive slope indicates positive acceleration, while a negative slope indicates negative acceleration or deceleration. The area under the velocity-time graph represents the displacement of the object.
Graphical representations of one-dimensional motion provide a clear and concise way to understand the relationship between different variables such as position, time, velocity, and acceleration. By analyzing these graphs, one can gain insights into the motion of an object and make predictions about its future behavior. Graphs also allow for easy comparison between different objects or different scenarios of motion, making them an invaluable tool in studying one-dimensional motion.
Practice Problems and Answer Key
In this section, you will find a series of practice problems related to the topic of motion in one dimension. These problems are designed to help you reinforce your understanding of the key concepts and equations associated with this topic. Each problem is accompanied by a detailed solution, which you can use as a reference to check your work.
Here are some examples of the practice problems you will find in this section:
- Problem 1: A car travels at a constant speed of 60 miles per hour for 3 hours. How far does the car travel?
- Problem 2: An object is dropped from a height of 100 meters. How long does it take for the object to reach the ground?
- Problem 3: A ball is thrown vertically upward with an initial velocity of 20 meters per second. How high does the ball go?
- Problem 4: A train accelerates from rest at a rate of 2 meters per second squared for 10 seconds. What is the final velocity of the train?
Each problem is accompanied by a step-by-step solution, explaining how to arrive at the correct answer. This will help you understand the process and apply it to similar problems in the future. Additionally, the solutions highlight the key equations and concepts used to solve the problems, providing you with a valuable review of the material.
By working through these practice problems and reviewing the solutions, you will strengthen your ability to apply the principles of motion in one dimension. This will enhance your problem-solving skills and prepare you for more complex problems that may arise in the future.