Geometry is a branch of mathematics that deals with the properties and relationships of shapes, lines, angles, and dimensions. In Chapter 2, you have learned various concepts and formulas related to geometric figures, such as triangles, quadrilaterals, and circles. Now, as you prepare for the test, it is essential to review the answers to the practice questions and exercises in order to solidify your understanding and improve your problem-solving skills.
During this chapter, you have explored the different types of triangles, including equilateral, isosceles, and scalene triangles. You have also learned about the properties of angles, such as complementary, supplementary, and vertical angles. Additionally, the chapter covers the characteristics of quadrilaterals, such as rectangles, squares, and parallelograms.
By reviewing the answers to the practice problems, you will gain a clearer understanding of the concepts and rules involved in geometry. This will enable you to solve problems more effectively and efficiently during the test. It is crucial to not only memorize the formulas but also understand how to apply them in various situations. Remember to show your work and explain your reasoning when solving problems, as this will demonstrate your understanding of the concepts and earn you more points.
Chapter 2 Test Review Geometry Answers
Preparing for a geometry test can be challenging, but with the right resources and practice, you can improve your understanding and performance. Here, you will find a review of the answers for the Chapter 2 test in geometry, which covers important concepts such as lines, angles, polygons, and circles.
1. Lines: In geometry, lines are defined as a straight path that extends in both directions without end. They can be represented by a lowercase letter or a pair of points on the line. Lines can intersect, creating points of intersection called intersections. When two lines intersect, they create angles.
2. Angles: An angle is formed by two rays that share a common endpoint called the vertex. Angles can be classified based on their measure. For example, acute angles have a measure less than 90 degrees, right angles have a measure of exactly 90 degrees, obtuse angles have a measure greater than 90 degrees but less than 180 degrees, and straight angles have a measure of 180 degrees.
3. Polygons: A polygon is a closed figure made up of straight line segments. The most common polygons are triangles, quadrilaterals, pentagons, hexagons, and octagons. Each of these polygons has specific properties, such as the sum of interior angles.
4. Circles: A circle is a closed curve in which all points are equidistant from the center. The radius is the distance between the center and any point on the circle, while the diameter is the distance across the circle passing through the center. The circumference is the distance around the circle, and the area is the space enclosed by the circle.
In conclusion, understanding the key concepts of lines, angles, polygons, and circles is crucial for success in geometry. By reviewing the answers for the Chapter 2 test, you can reinforce your knowledge and improve your performance. Practice solving problems and seeking additional resources to further enhance your understanding of geometry.
Basic Geometry Concepts
Geometry is the branch of mathematics that deals with the properties and relationships of points, lines, angles, surfaces, and solids. It is a fundamental subject that plays a crucial role in various fields, such as architecture, engineering, physics, and computer graphics. Understanding basic geometry concepts is essential for solving problems and analyzing geometric figures and shapes.
In geometry, points are the most basic elements. They have no size or shape and are represented by a dot. Points can be connected to form lines, which are infinitely long and have no width or thickness. Lines are denoted by two points on them, and they extend indefinitely in both directions. When two lines intersect, they form angles.
Angles are an important concept in geometry. They are formed by two lines or rays that meet at a common point called the vertex. Angles can be classified based on their measures. Acute angles are less than 90 degrees, right angles are exactly 90 degrees, obtuse angles are greater than 90 degrees but less than 180 degrees, and straight angles are exactly 180 degrees.
Triangles are three-sided polygons and a fundamental shape in geometry. They are classified based on the lengths of their sides and the measures of their angles. Equilateral triangles have three equal sides and three equal angles of 60 degrees. Isosceles triangles have two equal sides and two equal angles. Scalene triangles have no equal sides or angles.
Summary
- Geometry deals with points, lines, angles, surfaces, and solids.
- Points, lines, and angles are the basic elements in geometry.
- Angles are formed by two lines or rays meeting at a common vertex.
- Triangles are three-sided polygons with various classifications based on their sides and angles.
Understanding these basic concepts in geometry lays the foundation for further exploration and problem-solving in the field. By familiarizing ourselves with points, lines, angles, and triangles, we can navigate and analyze the geometric world around us more effectively.
Solving Geometric Equations
When it comes to solving geometric equations, there are several strategies and techniques that can be utilized. These equations involve various geometric shapes such as triangles, circles, and polygons, and their solutions help us find missing lengths, angles, or other properties of these shapes.
A common approach to solving geometric equations is to use the properties and relationships of the specific shape involved. For example, in a triangle, we can use properties such as the angle sum theorem or the Pythagorean theorem to find missing angles or sides. By applying these known relationships and equations, we can create an equation involving the unknown variable and solve for it.
Another important tool in solving geometric equations is algebra. By representing the given information and unknowns using variables, we can create equations that describe the relationships between these variables. We can then use algebraic techniques such as simplifying equations, combining like terms, or applying inverse operations to isolate the variable and find its value.
Furthermore, graphical methods can also be employed to solve geometric equations. This involves representing the geometric shapes and equations graphically on a coordinate plane and using the intersection points of the graphs to find the solutions. This approach is particularly useful when dealing with equations involving lines or conic sections.
In conclusion, solving geometric equations requires a combination of understanding the properties and relationships of the specific geometric shape, applying algebraic techniques to create equations, and utilizing graphical methods when applicable. By employing these strategies, we can effectively find solutions to geometric equations and gain a deeper understanding of the properties of geometric shapes.
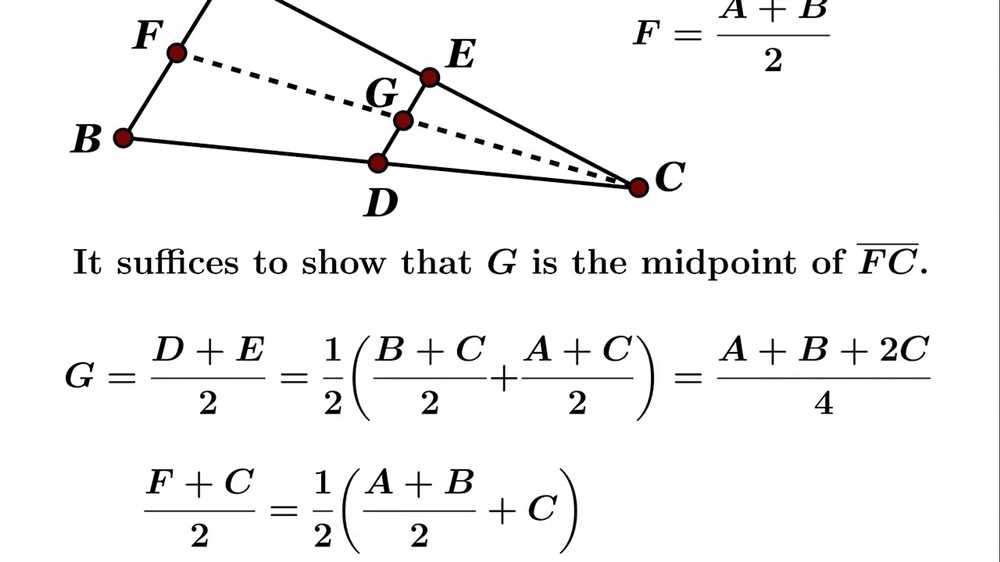
Triangle Properties and Theorems
Triangles are fundamental shapes in geometry with various properties and theorems. Understanding these properties and theorems is essential for solving geometric problems involving triangles.
Triangle Sum Theorem: The sum of the angles in any triangle is always 180 degrees. In other words, the three angles of a triangle add up to form a straight line.
Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is a useful tool for finding the length of a side in a right triangle when the lengths of the other sides are known.
Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side. This theorem helps determine the possible lengths of the sides of a triangle.
Triangle Congruence Theorems: There are several congruence theorems for triangles, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), and Hypotenuse-Leg (HL) theorems. These theorems state conditions under which two triangles are congruent, meaning they have the same shape and size.
Similar Triangles: Two triangles are similar if their corresponding angles are congruent and the ratios of the lengths of their corresponding sides are equal. Similar triangles have proportional sides and equal corresponding angles.
Triangle Midsegment Theorem: The segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length. This theorem can be used to find the length of a midsegment or the length of a side given the length of a midsegment.
Triangle Centers: There are several important points or centers in a triangle, including the centroid (the point of intersection of the medians), the circumcenter (the center of the circle that circumscribes the triangle), the incenter (the center of the circle that inscribes the triangle), and the orthocenter (the point of intersection of the altitudes).
In conclusion, understanding the properties and theorems related to triangles is crucial for solving geometric problems involving these fundamental shapes. These theorems help determine the relationships between angles, sides, and other elements of triangles, enabling us to accurately solve triangle-related problems.
Quadrilateral Properties and Theorems
Quadrilaterals are a type of polygon with four sides. They can be classified into different types based on their properties and characteristics. Understanding the properties and theorems about quadrilaterals is essential in solving geometry problems and proofs. Here are some important concepts to know:
1. Parallelogram: A parallelogram is a quadrilateral with opposite sides that are parallel. It has the following properties:
- Opposite sides are congruent
- Opposite angles are congruent
- Consecutive angles are supplementary
- Diagonals bisect each other
2. Rectangle: A rectangle is a parallelogram with four right angles. It has the following properties:
- All angles are right angles
- Opposite sides are congruent
- Diagonals are congruent and bisect each other
3. Rhombus: A rhombus is a parallelogram with four congruent sides. It has the following properties:
- All sides are congruent
- Opposite angles are congruent
- Diagonals are perpendicular bisectors of each other
4. Square: A square is a rectangle and a rhombus. It has all the properties of both:
- All angles are right angles
- All sides are congruent
- Diagonals are congruent and bisect each other
- Diagonals are perpendicular bisectors of each other
By understanding these properties and theorems, you can easily identify and work with different types of quadrilaterals in geometry problems and proofs.
Circles and Arcs
A circle is a geometric figure that consists of all points in a plane that are equidistant from a fixed center point. It can also be defined as the locus of points that are a fixed distance (radius) away from the center. The distance around the circle, or its circumference, is found using the formula C = 2πr, where π is a mathematical constant approximately equal to 3.14 and r is the radius of the circle.
An arc is a part of the circumference of a circle. It can be thought of as a portion of a curve between two points on the circle. The measure of an arc is given in degrees and can be calculated using the formula m(arc) = (θ/360) × 2πr, where θ is the central angle formed by the two endpoints of the arc and r is the radius of the circle. There are three types of arcs: minor arcs, major arcs, and semicircles.
In geometry, circles and arcs are important concepts that are used in various applications. They are commonly used in trigonometry, where the unit circle is used to define trigonometric functions. Circles are also used in many practical applications, such as in engineering and architecture, where they are used to design curved structures and calculate measurements for circular objects.
- A circle has several important properties, such as its diameter (twice the radius), chord (a line segment with both endpoints on the circle), and tangent (a line that touches the circle at only one point).
- When two circles intersect, they can create common chord, which is a line segment that is part of both circles. The length of the common chord can be calculated using the intersecting chords theorem.
- Arcs can be classified as congruent (having the same measure), adjacent (sharing an endpoint and a common chord), or intercepted (lying between two points on the circle).
Understanding circles and arcs is essential in geometry and has many practical applications in various fields. Whether it’s measuring the circumference of a circular object or designing curved structures, the concepts of circles and arcs are fundamental to solving geometric problems.
Area and Perimeter

When studying geometry, it is important to understand the concepts of area and perimeter. These two measurements are fundamental in determining the size and shape of two-dimensional figures.
Area refers to the amount of space inside a figure. It is calculated by multiplying the length and the width of a rectangle or the base and the height of a triangle. The result is expressed in square units (such as square inches or square centimeters).
Perimeter, on the other hand, is the total distance around the outside of a figure. It is calculated by adding up all the sides of the figure. For example, the perimeter of a rectangle can be found by adding twice the length and twice the width. The result is expressed in linear units (such as inches or centimeters).
It is important to note that area and perimeter are different measurements and serve different purposes. Area focuses on the amount of space enclosed within a figure, while perimeter focuses on the distance around the figure. Understanding these concepts is essential when solving problems and analyzing geometric figures.
When comparing figures, it is important to consider both area and perimeter. For example, two rectangles can have the same area but different perimeters. This means that they can have the same amount of space inside, but their shapes and the distances around them are different. Similarly, two rectangles can have the same perimeter but different areas, indicating that their shapes are different but the total distance around them is the same.