
Welcome to the Chapter 8 AP Stats Test! This comprehensive assessment is designed to evaluate your understanding of the statistical concepts and methods covered in Chapter 8 of the AP Statistics curriculum. In this chapter, we delve into the fascinating world of probability and explore various probability distributions.
Probability is a fundamental concept in statistics, allowing us to quantify and predict the likelihood of events occurring. In this test, you will encounter questions that test your ability to calculate probabilities, understand the properties of probability distributions, and apply probability concepts to real-life scenarios.
By taking this test, you will not only assess your knowledge and skills but also strengthen your understanding of probability. The questions in this test are carefully designed to challenge your critical thinking and problem-solving abilities, providing an opportunity for you to apply the statistical concepts you have learned.
Whether you are preparing for the AP Statistics exam or simply seeking to deepen your understanding of probability, the Chapter 8 AP Stats Test will serve as a valuable tool. Get ready to put your statistical knowledge to the test and explore the fascinating world of probability!
Chapter 8 AP Stats Test Preparation: Key Concepts and Tips
Preparing for the Chapter 8 AP Statistics test requires a solid understanding of key concepts related to statistical inference. In this chapter, students dive into hypothesis testing and confidence intervals, which are fundamental tools in drawing conclusions from data.
One of the key concepts to master is the idea of a null hypothesis and an alternative hypothesis. The null hypothesis represents the status quo or a claim that is to be tested, while the alternative hypothesis is the claim that contradicts the null hypothesis. Being able to correctly set up and interpret these hypotheses is crucial for hypothesis testing.
Another important concept is the p-value. The p-value is a measure of the strength of evidence against the null hypothesis. It is calculated based on the observed data and helps determine whether the results are statistically significant. Understanding how to interpret and use the p-value in hypothesis testing is essential.
Additionally, students should be familiar with confidence intervals. A confidence interval is an interval estimate of a parameter that is used to quantify the uncertainty of an estimate. It provides a range of plausible values for the parameter and allows for the assessment of precision. Knowing how to calculate and interpret confidence intervals is vital for drawing conclusions in statistical inference.
When preparing for the Chapter 8 AP Stats test, it is important to review these key concepts and practice applying them to different scenarios. Take the time to understand the underlying principles and formulas, and practice solving problems to build confidence in your ability to analyze and interpret data. Utilize resources such as textbooks, online tutorials, and practice exams to reinforce your understanding and identify areas that need further improvement. With dedication and thorough preparation, you will be well-equipped to tackle the Chapter 8 AP Stats test and succeed in your study of statistics.
Sampling Methods and Study Designs: Understanding the Basics
Sampling methods and study designs are essential concepts in statistics that enable researchers to gather data, analyze it, and draw conclusions about a larger population. These methods and designs help ensure that the data collected is representative and unbiased, allowing for accurate interpretations and generalizations.
There are various sampling methods that researchers can utilize, depending on the nature of their study and the population they are targeting. Simple random sampling, for example, involves selecting individuals from a population at random, giving each individual an equal chance to be chosen. This method is useful when studying a homogeneous population and provides a reliable representation.
Other commonly used sampling methods include:
- Stratified sampling: dividing the population into distinct subgroups and sampling from each subgroup proportionally.
- Cluster sampling: randomly selecting clusters or groups of individuals instead of individual units.
- Systematic sampling: selecting every nth individual from a population.
- Convenience sampling: selecting the most accessible individuals.
- Purposive sampling: intentionally selecting specific individuals who meet certain criteria.
Each sampling method has its advantages and limitations, and researchers must carefully consider which method is most appropriate for their study.
Study designs, on the other hand, refer to the overall plan or strategy that researchers use to conduct their study. The two main study designs are observational studies and experimental studies.
In an observational study, researchers observe and collect data without intervening or manipulating any variables. They simply observe and analyze the existing relationships between variables. This type of study design is useful when studying associations and correlations.
Experimental studies, on the other hand, involve intervention or manipulation of variables to assess cause-and-effect relationships. The researchers actively manipulate one or more variables and measure the effects on other variables. Experimental studies are often conducted in controlled environments, such as laboratories, to ensure accurate measurements.
Understanding sampling methods and study designs is crucial for any researcher or statistician to ensure the validity and reliability of their findings. By employing appropriate sampling methods and study designs, researchers can confidently draw conclusions and make informed decisions based on their data.
Probability and Sampling Distributions: Mastering the Fundamentals
The understanding of probability and sampling distributions is essential for mastering the fundamentals of statistics. Probability is the branch of mathematics that deals with the likelihood of events occurring. It allows us to quantify uncertainties and make informed decisions based on available information. In the context of statistics, probability enables us to analyze and interpret data, providing us with a framework to make statistical inferences.
Sampling distributions, on the other hand, play a crucial role in hypothesis testing and estimation. They allow us to study the characteristics of samples drawn from a population and make inferences about the population parameters. By repeatedly sampling from a population, we can observe how sample statistics vary and use this information to make generalizations about the larger population. Understanding sampling distributions helps us make informed decisions about the validity of our statistical analyses and the accuracy of our estimates.
In probability, we rely on mathematical principles and formulas to determine the likelihood of various events occurring. We use concepts such as probability rules, conditional probability, and independence to analyze data and calculate probabilities. These concepts are fundamental to statistical analysis and can be applied to a wide range of scenarios.
Sampling distributions, on the other hand, involve the concept of randomness. By randomly sampling from a population, we attempt to capture the characteristics of the larger population. The process of sampling introduces variability, and sampling distributions help us understand how this variability affects our estimates and inferences.
In summary, probability and sampling distributions are essential components of statistics. Probability allows us to quantify uncertainties and make informed decisions, while sampling distributions help us understand the characteristics of samples and make inferences about populations. Mastering the fundamentals of probability and sampling distributions is crucial for becoming proficient in statistical analysis and drawing valid conclusions from data.
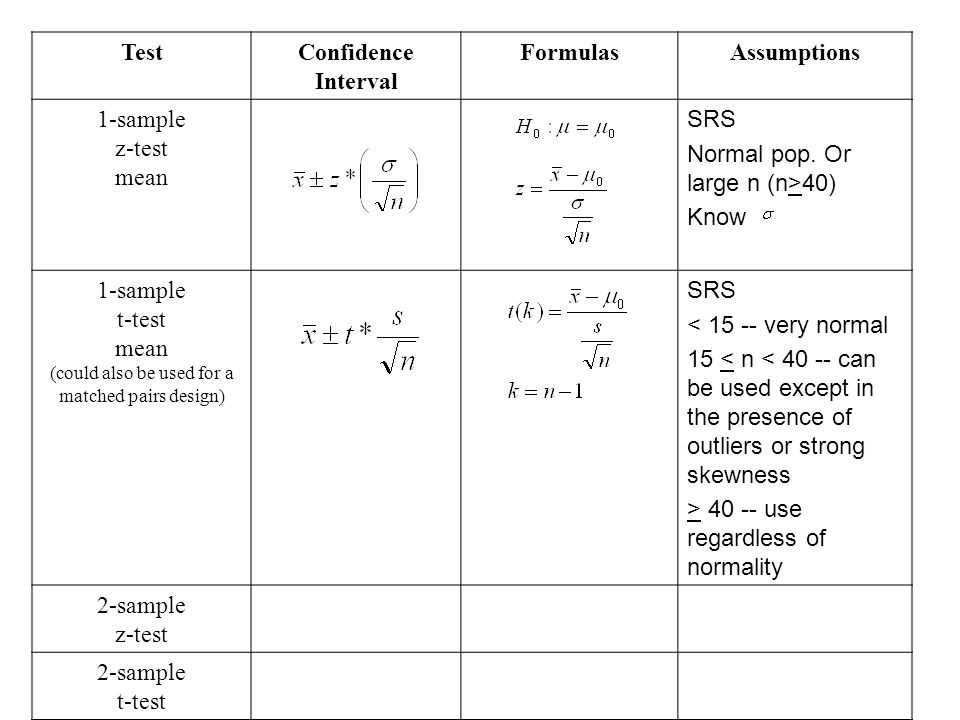
Confidence Intervals: Estimation with Precision
Confidence intervals play a crucial role in statistical inference as they provide a range within which a population parameter is estimated to lie with a certain level of confidence. These intervals are constructed based on sample data, allowing us to make statements about the population as a whole. The goal is not just to estimate the parameter, but also to quantify the level of uncertainty associated with the estimate.
When constructing a confidence interval, it is important to consider both the sample size and the desired level of confidence. A larger sample size generally leads to a narrower interval, indicating a more precise estimate. On the other hand, a higher confidence level, such as 95% or 99%, leads to wider intervals, allowing for a greater level of certainty that the true population parameter falls within the interval.
To calculate a confidence interval, a common approach is to use a formula based on the standard error of the estimate. The standard error takes into account the sample size, variability of the data, and the sampling distribution. By multiplying the standard error by a critical value, which depends on the desired confidence level, we can determine the margin of error for the estimate. The margin of error is then used to calculate the lower and upper bounds of the confidence interval.
In conclusion, confidence intervals provide us with both an estimate of a population parameter and an indication of the precision of that estimate. They are essential tools in statistical analysis, helping us make informed decisions based on sample data.
Chi-Square Tests: Analyzing Categorical Data
In statistics, chi-square tests are used to analyze categorical data and determine if there is a significant association or difference between two or more categorical variables. These tests are based on the chi-square statistic, which measures the discrepancy between the observed frequencies and the expected frequencies under the null hypothesis.
The chi-square tests can be used to analyze various types of categorical data, such as proportions, counts, or frequencies. Some common applications of chi-square tests include testing for independence in contingency tables, comparing observed and expected frequencies, and testing goodness-of-fit to a specific distribution.
A chi-square test for independence is used to determine if there is a relationship between two categorical variables. This test is conducted using a contingency table, which displays the frequencies or proportions of observations for each combination of categories from the two variables. The chi-square test calculates the expected frequencies assuming independence and compares them to the observed frequencies to determine if there is a significant association.
Another application of chi-square tests is testing for goodness-of-fit, which is used to determine if the observed frequencies of a categorical variable fit a specific distribution. This test compares the observed frequencies to the expected frequencies under the null hypothesis of the specified distribution. If the chi-square statistic is significantly large, it indicates that the observed frequencies deviate from the expected frequencies and there may be a significant difference.
Regression Analysis: Predicting and Explaining Relationships
Regression analysis is a statistical technique used to predict and explain relationships between variables. It involves finding the best-fitting line or curve that represents the relationship between a dependent variable (also known as the response variable) and one or more independent variables (also known as predictor variables or explanatory variables).
The goal of regression analysis is to develop a mathematical model that can accurately predict the value of the dependent variable based on the values of the independent variables. This model can then be used to make predictions or explain the relationship between the variables. It is particularly useful when we want to understand how changes in one variable affect another variable, or when we want to forecast future values based on historical data.
In regression analysis, the relationship between variables is represented by a regression equation, which is typically written as follows:
Y = β0 + β1X1 + β2X2 + … + βnXn + ε
Where:
- Y is the dependent variable (response variable).
- β0 is the y-intercept (the value of Y when all the predictor variables are set to zero).
- β1, β2, … βn are the coefficients (also known as slopes), which represent the change in Y associated with a one-unit change in the corresponding X variable.
- X1, X2, … Xn are the independent variables (predictor variables or explanatory variables).
- ε is the error term, which accounts for the random and unexplained variation in Y that cannot be accounted for by the predictor variables.
In summary, regression analysis is a powerful tool for predicting and explaining relationships between variables. By fitting a regression model to data, we can quantify the impact of independent variables on the dependent variable, make predictions, and gain insights into the underlying relationships. It is widely used in various fields, including economics, finance, social sciences, and marketing, to name just a few.
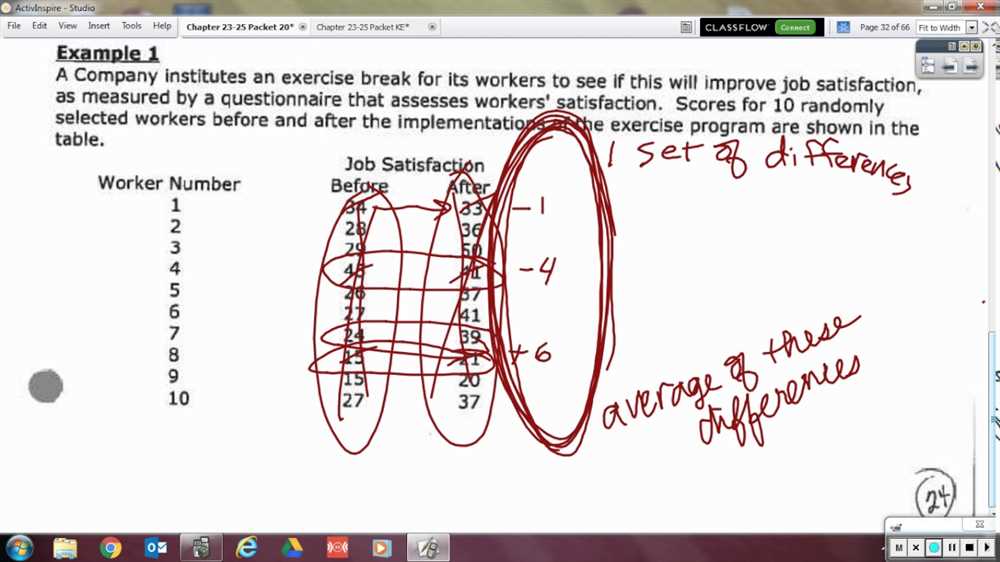
Experimental Design: Controlling Variables and Analyzing Results
Experimental design is a crucial aspect of any scientific study, as it allows researchers to control variables and analyze the results in a meaningful way. By carefully designing an experiment, researchers can ensure that any observed effects or differences can be attributed to the variables they are interested in studying.
One key step in experimental design is controlling variables. This involves identifying and controlling any factors that may potentially influence the outcome of the study, other than the variables of interest. For example, if a researcher is studying the effects of a new drug on blood pressure, they may need to control factors such as age, gender, and lifestyle habits to ensure that any observed changes in blood pressure can be attributed to the drug and not other factors.
Another important aspect of experimental design is analyzing the results. After collecting data, researchers can use statistical methods to analyze and interpret the data. This typically involves comparing groups or conditions to determine if there are any significant differences or relationships. Statistical tests such as t-tests, ANOVA, or regression analysis can be used to determine if the observed differences are statistically significant, and to quantify the strength of the relationship between variables.
- In conclusion, experimental design plays a crucial role in scientific research, allowing researchers to control variables and analyze results.
- By carefully controlling variables, researchers can ensure that any observed effects can be attributed to the variables of interest.
- Additionally, analyzing the results using statistical methods allows researchers to determine the significance of any observed differences or relationships.