
In Chapter 8 of the textbook, we delve into the world of quadratic functions and equations. This chapter focuses on understanding the properties and behaviors of quadratic functions, as well as finding solutions to quadratic equations. Quadratic functions are those that can be expressed in the form of f(x) = ax^2 + bx + c, where a, b, and c are constants.
Throughout the chapter, you will learn how to graph quadratic functions, identify key features such as the vertex and axis of symmetry, and analyze the concavity of the graph. Understanding these features will allow you to make predictions about the behavior of the function, such as whether it opens up or down and the location of the minimum or maximum point.
In addition to graphing and analyzing quadratic functions, this chapter also covers solving quadratic equations. These equations are those that can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants. You will learn various methods for solving quadratic equations, including factoring, completing the square, and using the quadratic formula. Each method has its advantages and disadvantages, and it is important to understand when and how to use each one.
By the end of Chapter 8, you will have a solid understanding of quadratic functions and equations, as well as the skills needed to graph and solve them. The answer key provided will allow you to check your work and ensure that you are on the right track. Whether you are preparing for a test or simply looking to deepen your understanding of quadratic functions, this chapter will provide you with the necessary tools and resources.
Chapter 8 Quadratic Functions and Equations Answer Key

In Chapter 8 of our textbook, we focused on quadratic functions and equations, which are an important topic in algebra. This answer key provides solutions to the exercises and problems presented in this chapter, allowing students to check their work and gain a better understanding of the concepts covered.
Quadratic functions are polynomial functions of degree 2, which means they have a second-degree term. These functions can be represented by the general equation f(x) = ax^2 + bx + c, where a, b, and c are constants. In this chapter, we learned how to graph quadratic functions, identify the vertex and axis of symmetry, determine the maximum or minimum value, and find the x-intercepts or roots.
The answer key for Chapter 8 includes step-by-step solutions to various types of problems, such as finding the vertex of a parabola, solving quadratic equations by factoring or using the quadratic formula, and applying quadratic functions to real-world situations. It also provides explanations and tips to help students grasp the underlying concepts and apply them effectively.
By using the answer key, students can verify their answers, identify any mistakes they made, and learn from them. It serves as a valuable resource for self-assessment and self-correction, allowing students to track their progress and improve their problem-solving skills. The answer key can also be used by teachers as a tool for grading assignments and providing additional guidance to students.
Overall, the Chapter 8 Quadratic Functions and Equations Answer Key plays an essential role in helping students master the concepts and techniques related to quadratic functions and equations. It serves as a reliable reference and learning tool, enabling students to build a solid foundation in algebra and prepare for more advanced topics in mathematics.
Understanding Quadratic Functions
Quadratic functions play a crucial role in mathematics and are extensively studied in algebra. These functions are represented by equations of the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which can be concave up or concave down depending on the value of the coefficient a.
A key concept in understanding quadratic functions is the vertex, which is the point on the parabola where it reaches its minimum or maximum. The vertex can be found using the formula x = -b/2a, which gives the x-coordinate, and substituting this value into the equation gives the corresponding y-coordinate.
Quadratic functions also have important properties such as the axis of symmetry, which is the vertical line passing through the vertex. This line divides the parabola into two symmetric halves. Another important property is the y-intercept, which is the point where the parabola intersects the y-axis. This can be found by substituting x = 0 into the equation.
In addition to these properties, quadratic functions can be used to solve a variety of real-world problems. For example, they can be used to model the trajectory of a projectile, the growth of a population, or the profit and loss of a business. By understanding quadratic functions and their properties, we can analyze and solve these types of problems.
Graphing Quadratic Functions
A quadratic function is a polynomial function of the second degree, meaning it has the form:
f(x) = ax^2 + bx + c
The graph of a quadratic function is a parabola. It has a distinct U-shape and can open upward or downward. The direction of the opening depends on the coefficient a in the function.
To graph a quadratic function, it is essential to identify its key features, including the vertex, axis of symmetry, and x-intercepts (also known as zeros or roots). The vertex form of a quadratic function is helpful in understanding these features:
f(x) = a(x – h)^2 + k
where (h, k) represents the coordinates of the vertex. The axis of symmetry is a vertical line passing through the vertex, and the x-intercepts are the points where the graph intersects the x-axis.
In order to graph a quadratic function, start by calculating the vertex using the formula:
h = -b/2a
Once the vertex is determined, plot it on the coordinate plane. Then, find the x-intercepts by setting the quadratic function equal to zero and solving for x. Use these points to draw the parabolic curve.
Understanding how to graph quadratic functions is crucial for analyzing real-world situations and solving problems involving quadratic equations. It allows us to visualize the behavior of the function and make predictions about its values at different input values.
Furthermore, graphing quadratic functions helps in identifying the maximum or minimum values of the function and determining its range. It also assists in finding the solutions to quadratic equations, which can be useful in various fields such as physics, engineering, and finance.
Solving Quadratic Equations Algebraically

The process of solving quadratic equations algebraically involves finding the values of x that make the equation true. Quadratic equations are those in the form of ax^2 + bx + c = 0, where a, b, and c are constants. There are several methods to solve these equations algebraically, including factoring, using the quadratic formula, and completing the square.
Factoring: One method to solve quadratic equations is through factoring. This involves finding two binomials that, when multiplied, equal the quadratic equation. By setting each binomial equal to zero, you can find the values of x. However, factoring may not always be possible, especially for more complex equations.
Quadratic Formula: The quadratic formula is another powerful tool for solving quadratic equations algebraically. The formula states that given a quadratic equation ax^2 + bx + c = 0, the solutions for x are given by the formula x = (-b ± √(b^2 – 4ac)) / 2a. By plugging in the values for a, b, and c, you can find the solutions for x. This method is particularly useful when factoring is not feasible.
Completing the Square: Completing the square is a method that involves rearranging the terms of a quadratic equation to create a perfect square trinomial. This can then be easily factored or solved algebraically. The process involves adding or subtracting a constant to both sides of the equation to create a square trinomial. This method is often used in conjunction with the quadratic formula to solve quadratic equations.
In conclusion, solving quadratic equations algebraically involves using various methods such as factoring, the quadratic formula, and completing the square. These methods allow us to find the values of x that satisfy the equation. It is important to practice and understand these methods in order to effectively solve quadratic equations and apply them to real-life scenarios.
Factoring Quadratic Equations
Factoring quadratic equations is an important skill in algebra, especially when solving for the roots or zeros of a quadratic function. By factoring a quadratic equation, we can express it as the product of two binomials. This allows us to easily find the values of x that make the equation equal to zero.
To factor a quadratic equation, we look for two binomials whose product is equal to the quadratic equation. This can be done by using methods such as the AC method, the trial and error method, or by using special formulas like the difference of squares or perfect square trinomials.
Once we have factored the quadratic equation, we can set each binomial equal to zero and solve for x. The values of x that make each binomial equal to zero are the solutions or roots of the quadratic equation. These solutions can be real or complex numbers, depending on the discriminant of the quadratic equation.
Factoring quadratic equations is useful in various applications such as finding the x-intercepts of a parabola, determining the factors of a polynomial, solving word problems involving quadratic equations, and simplifying complex expressions.
In conclusion, factoring quadratic equations is a powerful technique that allows us to solve for the roots or zeros of a quadratic function. By factoring the quadratic equation into two binomials, we can easily find the values of x that satisfy the equation. This skill is essential in algebra and has practical applications in various mathematical and real-world situations.
Using the Quadratic Formula
The quadratic formula is a powerful tool in solving quadratic equations. It is an algebraic formula that can be used to find the roots or solutions of any quadratic equation in the form of ax^2 + bx + c = 0. The formula is:
x = (-b ± √(b^2 – 4ac)) / 2a
Here, x represents the variable we are trying to solve for, and a, b, and c are the coefficients of the quadratic equation. The two solutions obtained from the quadratic formula are called the roots of the equation.
By plugging the coefficients of the quadratic equation into the formula, we can find the values of x that make the equation true. The formula allows us to find the roots of any quadratic equation, whether it has real or complex solutions.
When using the quadratic formula, we must first identify the values of a, b, and c in the given equation. Then, we substitute these values into the quadratic formula and simplify the equation to find the solutions for x.
After finding the values of x, we can check our solutions by substituting them back into the original equation and verifying if they satisfy the equation. This step is important to ensure the accuracy of our solutions.
The quadratic formula is an essential tool in solving quadratic equations and is often taught in algebra classes. It provides a systematic and reliable method for finding the roots of quadratic equations, making it a valuable tool in various math and science applications.
Applying Quadratic Functions to Real-World Problems

In the world of mathematics, quadratic functions are widely used to solve real-world problems. These functions are particularly useful in modeling and analyzing various situations that involve a parabolic curve. By understanding and applying quadratic functions, we can make predictions, optimize outcomes, and solve problems efficiently.
One common application of quadratic functions is in projectile motion problems. When an object is launched into the air, its path can be modeled by a quadratic function. By determining the initial velocity, angle of launch, and height, we can predict the maximum height reached by the object, its range, and its time of flight. This information is crucial in fields such as physics and engineering, where understanding the trajectory of projectiles is essential for designing and optimizing systems.
Another practical application of quadratic functions is in the field of finance. For example, quadratic functions can be used to model revenue and profit in business scenarios. By analyzing the cost and demand function, businesses can determine the optimal price and quantity to maximize their profit. Quadratic functions are also used in portfolio optimization, where investors aim to construct an investment portfolio that maximizes returns given a certain level of risk.
In conclusion, quadratic functions play a crucial role in solving real-world problems across various disciplines. Whether it’s predicting projectile motion, optimizing business outcomes, or managing financial investments, understanding and applying quadratic functions can provide valuable insights and solutions. By utilizing the power of mathematics, we can make informed decisions and drive innovation in a wide range of industries.
Completing the Square
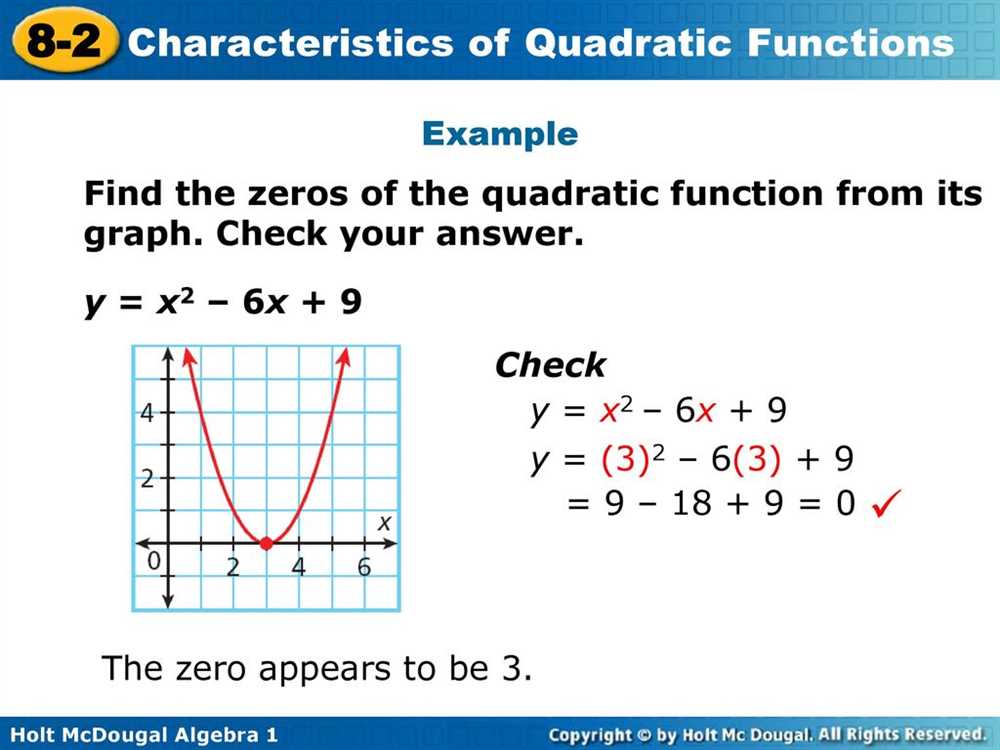
Completing the square is a technique used to solve quadratic equations and to transform quadratic functions into a more easily solvable form. It involves rearranging the terms of a quadratic equation to create a perfect square trinomial.
The process of completing the square involves three main steps. First, we make sure that the coefficient of the quadratic term is equal to 1. If it is not, we divide the entire equation by the coefficient. Second, we isolate the quadratic and linear terms on one side of the equation. Finally, we add a constant term to both sides of the equation in order to complete the square.
To illustrate this process, let’s consider an example. Suppose we have the quadratic equation: x^2 + 6x + 9 = 0. First, we divide by the coefficient of the quadratic term, which is 1, so we are left with: x^2 + 6x + 9 = 0. Next, we isolate the quadratic and linear terms on one side of the equation: (x + 3)^2 = 0. Finally, we add 9 to both sides of the equation to complete the square: (x + 3)^2 + 9 = 9. This gives us the perfect square trinomial (x + 3)^2 = 9.
Completing the square is a valuable tool in solving quadratic equations, as it allows us to easily factorize quadratic expressions and find their solutions. It is also important in graphing quadratic functions, as it helps us determine the vertex and axis of symmetry. By completing the square, we can transform a quadratic function into vertex form, which provides us with valuable information about the shape and position of the graph.