
When learning about real numbers, it is important to have a clear understanding of their classifications. Real numbers can be classified into several categories based on their properties and characteristics. This classification helps us to better understand the relationships between different types of numbers and how they can be manipulated in mathematical operations.
The real numbers can be divided into three main categories: rational numbers, irrational numbers, and integers. Rational numbers are numbers that can be expressed as a fraction or a ratio of two integers. They can be either positive, negative, or zero. Irrational numbers, on the other hand, cannot be expressed as a fraction and have an infinite number of non-repeating decimal places. Integers are whole numbers that can be either positive, negative, or zero.
To classify real numbers, it is important to understand the properties and characteristics of each category. Rational numbers can be further classified into integers, fractions, mixed numbers, and terminating or repeating decimals. Irrational numbers include numbers such as π and √2, which cannot be expressed as fractions or ratios. Integers are whole numbers that do not have a fractional or decimal part.
This classifying real numbers worksheet answer key provides a comprehensive guide to understanding and categorizing different types of real numbers. It includes examples and explanations to help students grasp the concepts more easily. By practicing with this worksheet, students can improve their knowledge and skills in classifying real numbers, which is essential for solving complex mathematical problems.
Real numbers: an overview
The concept of real numbers is fundamental in mathematics and plays a crucial role in various fields such as algebra, calculus, and number theory. Real numbers encompass a wide range of values including integers, fractions, decimals, and irrational numbers.
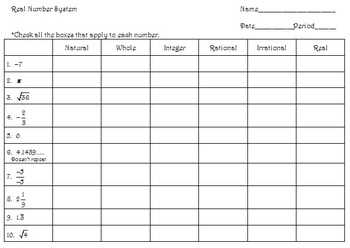
Real numbers can be classified into five main categories: natural numbers, whole numbers, integers, rational numbers, and irrational numbers. Natural numbers are the positive counting numbers (1, 2, 3, …). Whole numbers include the natural numbers along with zero (0, 1, 2, 3, …). Integers consist of the whole numbers and their negative counterparts (-3, -2, -1, 0, 1, 2, 3, …).
Rational numbers are numbers that can be expressed as a ratio of two integers. They can be either terminating or recurring decimals (3.5, -1.25, 2.333…). Irrational numbers, on the other hand, cannot be expressed as a fraction and have non-repeating decimal expansions (π, √2).
A key property of real numbers is their ability to be ordered on a number line. This allows us to compare and place real numbers in relation to one another. For example, we can determine that 2 is greater than -3, or that √2 is between 1 and 2 on the number line.
Understanding and classifying real numbers is essential for solving mathematical problems, analyzing data, and making informed decisions. Whether it’s calculating distances, estimating probabilities, or solving equations, the concept of real numbers underpins many mathematical concepts and applications.
The Importance of Classifying Real Numbers

Classifying real numbers is an essential concept in mathematics as it allows us to organize and understand the different types of numbers that exist. Real numbers include rational numbers, which can be expressed as a fraction, and irrational numbers, which cannot be expressed as a fraction and have an infinite number of non-repeating decimal places. By classifying real numbers, we can better analyze and solve mathematical problems, as well as gain a deeper understanding of the relationships between different types of numbers.
One of the main reasons for classifying real numbers is to identify patterns and relationships. Classifying numbers into rational and irrational categories helps us identify common characteristics and properties that are unique to each group. For example, rational numbers can be classified further into integers, which are whole numbers, and fractions, which are numbers that can be expressed as a ratio. By understanding these classifications, we can better understand how numbers interact with each other and how they can be manipulated in mathematical equations.
Another reason why classifying real numbers is important is for problem-solving purposes. In mathematics, it is often necessary to determine if a given number is rational or irrational in order to solve an equation or verify the accuracy of a solution. By classifying real numbers, we can quickly identify which operations and methods are applicable to a particular number, making problem-solving more efficient and effective.
In conclusion, classifying real numbers is a fundamental concept in mathematics that helps us organize and understand the various types of numbers that exist. It allows us to identify patterns and relationships, as well as solve mathematical problems more efficiently. By gaining a deeper understanding of the classifications of real numbers, we can enhance our overall mathematical skills and knowledge.
Understanding the different types of real numbers
Real numbers are a fundamental concept in mathematics, and they can be divided into several different types. The key to understanding real numbers is to recognize their distinct characteristics and properties. By classifying real numbers into specific categories, mathematicians can effectively study and analyze various mathematical problems and equations.
1. Rational Numbers: Rational numbers are those that can be expressed as a fraction of two integers. They can be written in the form of p/q, where p and q are integers and q is not equal to zero. Examples of rational numbers include -1/2, 3/4, and 5/1. Rational numbers can also be written in decimal form, where they either terminate or repeat.
2. Irrational Numbers: Irrational numbers are those that cannot be expressed as a fraction of two integers. They are decimal numbers that do not terminate or repeat. Examples of irrational numbers include √2, π, and e. The decimal representation of irrational numbers is infinite and non-repeating.
3. Integer Numbers: Integer numbers are whole numbers that do not have a fractional or decimal part. They include positive numbers, negative numbers, and zero. Examples of integer numbers include -3, 0, and 6. Integer numbers can be classified as either positive or negative.
4. Whole Numbers: Whole numbers are similar to integer numbers but do not include negative numbers. They are non-negative numbers that include zero and all positive integers. Examples of whole numbers include 0, 1, and 7. Whole numbers are a subset of integer numbers.
5. Natural Numbers: Natural numbers are the most basic type of real numbers. They are positive integers starting from 1 and do not include zero or negative numbers. Examples of natural numbers include 1, 2, and 10. Natural numbers are a subset of both whole and integer numbers.
Why is classifying real numbers important?
Classifying real numbers is an essential skill in mathematics as it helps us understand and organize the different types of numbers that exist. By classifying real numbers, we can determine their properties and relationships, which are crucial for solving mathematical problems and making accurate calculations.
One reason why classifying real numbers is important is that it allows us to identify and classify the different subsets of numbers, such as natural numbers, whole numbers, integers, rational numbers, and irrational numbers. Each of these subsets has its own distinct characteristics and properties, and by understanding these classifications, we can better understand how these numbers behave and interact.
Another reason why classifying real numbers is important is that it helps us make sense of real-world situations and solve practical problems. For example, when working with measurements, it is crucial to know whether a given number is a rational number or an irrational number, as this can affect the accuracy of our calculations. Additionally, classifying real numbers is necessary when dealing with financial transactions, probability, and statistics, where the different subsets of numbers have specific applications and interpretations.
Overall, the ability to classify real numbers is a fundamental skill in mathematics that provides a solid foundation for further learning and problem-solving. It allows us to understand the properties and relationships of numbers, make accurate calculations, and apply mathematical concepts to real-world situations. Therefore, mastering the classification of real numbers is essential for any student of mathematics.
Classifying real numbers: the classification system

In mathematics, real numbers can be classified into different categories based on their properties and characteristics. This classification system helps us understand the nature and behavior of these numbers, and it plays a crucial role in various fields of study, including algebra, calculus, and geometry.
The classification of real numbers is based on several factors, including their position on the number line, their relationship with other numbers, and their algebraic properties. Understanding this classification system is essential for solving problems and performing computations involving real numbers.
One way to classify real numbers is based on their position on the number line. For example, we have positive numbers, which are greater than zero, and negative numbers, which are less than zero. Zero itself is also considered a real number, and it is neither positive nor negative. Another category is rational numbers, which can be expressed as a fraction of two integers. Irrational numbers, on the other hand, cannot be expressed as a fraction and have an infinite non-repeating decimal representation.
Another way to classify real numbers is based on their relationship with other numbers. For example, we have integers, which are whole numbers (both positive and negative) and their zero. Integers are a subset of rational numbers, as every integer can be expressed as a fraction with denominator 1. Similarly, rational numbers are a subset of real numbers, as every rational number can be represented on the number line.
Finally, real numbers can also be classified based on their algebraic properties. For example, we have algebraic numbers, which are the roots of polynomial equations with integer coefficients. Transcendental numbers, on the other hand, cannot be the roots of any such polynomial equation. This classification is important in the study of number theory and algebra.
In conclusion, the classification of real numbers provides us with a systematic way to categorize and understand these numbers. It allows us to make connections between different types of numbers and apply them in various mathematical contexts. By understanding the classification system, we can better navigate the world of real numbers and solve complex mathematical problems.
Rational Numbers

Rational numbers are a subset of real numbers that can be expressed as a fraction or a ratio of two integers. The key characteristic of rational numbers is that they can be written as a quotient of two integers, where the denominator is not zero.
Rational numbers can be positive, negative, or zero. They can also be whole numbers, integers, or fractions. For example, the numbers 3, -2, 0, 1/2, and -5/3 are all rational numbers. The decimal representation of rational numbers can either terminate or repeat indefinitely. For instance, 0.25 and 0.3333… are both rational numbers.
One way to classify rational numbers is by comparing them to irrational numbers. Unlike rational numbers, irrational numbers cannot be expressed as a ratio of two integers. Instead, they have non-repeating and non-terminating decimal representations. Examples of irrational numbers include √2, π, and e.
Rational numbers have several important properties. They can be added, subtracted, multiplied, and divided, and the result is always a rational number. Division by zero, however, is not defined for rational numbers. Rational numbers also obey the commutative, associative, and distributive laws of arithmetic.
In conclusion, rational numbers are an important subset of real numbers that can be expressed as a fraction or ratio of two integers. They can be positive, negative, or zero, and their decimal representation can either terminate or repeat. Rational numbers can be compared to irrational numbers, which cannot be expressed as a ratio of two integers. Understanding rational numbers and their properties is fundamental in mathematics and has applications in various fields.
Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as a fraction or a ratio of two integers. They are numbers that cannot be written as terminating or repeating decimals. Irrational numbers are often represented by non-repeating, non-terminating decimals.
One well-known example of an irrational number is π (pi). Pi represents the ratio of a circle’s circumference to its diameter and is approximately equal to 3.14159. The decimal representation of pi goes on forever without repeating or terminating. Another example of an irrational number is the square root of 2 (√2). It is approximately equal to 1.41421. The decimal representation of √2 also goes on forever without repeating or terminating.
Irrational numbers are important in mathematics and have various applications in different fields, such as geometry, physics, and engineering. They play a crucial role in calculations involving measurements, equations, and mathematical models. Understanding irrational numbers and their properties is essential for solving complex mathematical problems and equations.
- Irrational numbers cannot be expressed as fractions or ratios of integers.
- The decimal representation of irrational numbers goes on forever without repeating or terminating.
- Important examples of irrational numbers include π and the square root of 2 (√2).
- Irrational numbers have various applications in mathematics and different fields of study.
Overall, irrational numbers are a fundamental concept in mathematics and have significant implications in real-world applications. They provide a deeper understanding of the infinite and complex nature of numbers, and they are essential for solving a wide range of mathematical problems and equations.