
Mathematical concepts and calculations involving angles often require converting between degrees and radians. It is crucial for students to practice these conversions and understand the relationship between these two units of measuring angles. To help with this practice, we have provided an answer key to guide students in checking their conversions and understanding the process.
The conversion between degrees and radians involves multiplying or dividing by conversion factors. One full circle in degrees is equal to 360 degrees, while one full circle in radians is equal to 2π radians. To convert degrees to radians, students multiply the degree measurement by π/180. Conversely, to convert radians to degrees, students multiply the radian measurement by 180/π. Understanding these conversion factors enables students to solve various mathematical problems seamlessly.
Using the provided answer key, students can verify their calculations and ensure they are on the right track. It breaks down the step-by-step process of converting between degrees and radians, allowing students to identify any mistakes and learn from them. By practicing with this answer key, students can enhance their understanding of angular measurement and tackle more complex problems involving degrees and radians confidently.
Degrees and Radians Conversion Practice Answer Key
Below is the answer key for the degrees and radians conversion practice:
1. Convert 45 degrees to radians:
The conversion formula is: radians = (degrees * π) / 180
In this case, the calculation would be: (45 * π) / 180 = 0.7854 radians
2. Convert 180 degrees to radians:
The conversion formula is: radians = (degrees * π) / 180
In this case, the calculation would be: (180 * π) / 180 = 3.1416 radians
3. Convert 3π/4 radians to degrees:
The conversion formula is: degrees = (radians * 180) / π
In this case, the calculation would be: (3π/4 * 180) / π = 135 degrees
- 4. Convert 90 degrees to radians:
- The conversion formula is: radians = (degrees * π) / 180
- In this case, the calculation would be: (90 * π) / 180 = 1.5708 radians
5. Convert 2π radians to degrees:
The conversion formula is: degrees = (radians * 180) / π
In this case, the calculation would be: (2π * 180) / π = 360 degrees
Remember, it’s important to practice converting between degrees and radians to become comfortable with both systems of measurement.
Understanding the Relationship between Degrees and Radians
In mathematics, degrees and radians are two common units for measuring angles. While degrees are more commonly used in everyday life, radians are often preferred in higher-level mathematics and physics because they simplify many mathematical equations.
As a measurement of an angle, a degree is defined as 1/360th of a full circle. A full circle consists of 360 degrees, and each degree is further divided into 60 minutes, and each minute is divided into 60 seconds. Therefore, the smallest unit of measurement in degrees is a second.
On the other hand, a radian is defined as the measure of an angle subtended by an arc of a circle that is equal in length to the radius of the circle. In simpler terms, a radian is the angle that spans an arc with a length equal to the radius of the circle. Since the circumference of a circle is 2π times the radius, a full circle contains 2π radians. This relationship between radians and the circumference of a circle is what makes radians a useful unit in mathematics.
To convert between degrees and radians, we can use the fact that a full circle contains 360 degrees or 2π radians. Therefore, to convert from degrees to radians, we can simply multiply the angle in degrees by π/180. Conversely, to convert from radians to degrees, we can multiply the angle in radians by 180/π.
Understanding the relationship between degrees and radians is essential in many areas of mathematics and physics. For example, when dealing with circular motion, trigonometric functions often require angles to be in radians. By converting between degrees and radians, we can work with angles more conveniently and efficiently in different mathematical contexts.
Converting Degrees to Radians
When working with angles, it is often necessary to convert between degrees and radians. Radians are a unit of measurement for angles in the context of a circle. One radian is equal to the angle subtended by an arc of length equal to the radius of the circle. On the other hand, degrees are a more common unit of measurement for angles in everyday life.
To convert degrees to radians, you can use the formula:
- Radians = (Degrees * π) / 180
For example, let’s say you have an angle of 45 degrees. To convert this angle to radians, you would use the formula:
- Radians = (45 * π) / 180
After simplifying the expression, you would find that the angle is approximately 0.7854 radians. This means that the angle of 45 degrees is equivalent to approximately 0.7854 radians.
It’s important to note that radians are often preferred over degrees in mathematical calculations because they simplify trigonometric functions and make them easier to work with. So, being able to convert between degrees and radians is a valuable skill for anyone working with angles and trigonometry.
Practice Questions: Converting Degrees to Radians
In mathematics, radians are commonly used to measure angles. However, degrees are also widely used, especially in everyday life. Converting between degrees and radians is an essential skill for anyone studying or working with angles. Here are some practice questions to help you develop your conversion skills from degrees to radians:
Question 1:
Convert 45 degrees to radians.
Answer: To convert degrees to radians, we use the formula: radians = (degrees * π) / 180. Therefore, for 45 degrees, the conversion would be (45 * π) / 180 = 0.7854 radians.
Question 2:
What is the equivalent value of 180 degrees in radians?
Answer: Using the same formula, we can calculate that 180 degrees is equivalent to (180 * π) / 180 = π radians.
Question 3:
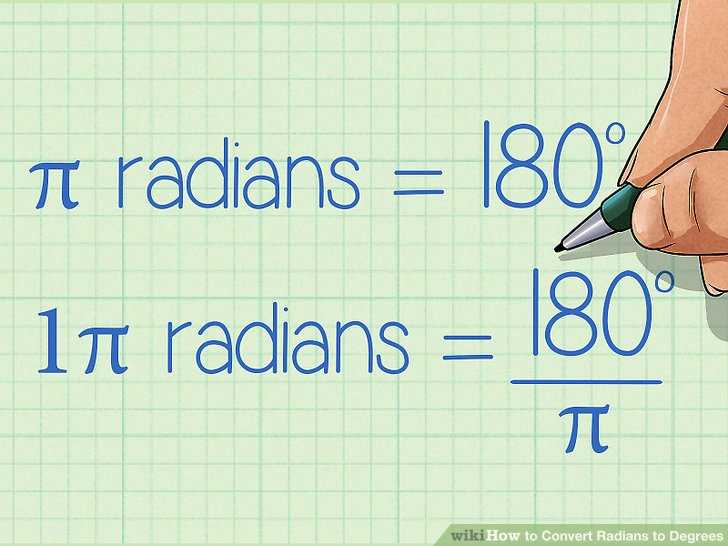
If an angle measures 360 degrees, what is its value in radians?
Answer: Applying the conversion formula, we find that 360 degrees is equal to (360 * π) / 180 = 2π radians.
Remember, the conversion factor from degrees to radians is π / 180. By practicing similar questions, you can become more familiar with the conversion process and improve your understanding of angles in both degrees and radians.
Answer Key: Converting Degrees to Radians
Below is the answer key for converting degrees to radians. This key provides the correct conversion values for a range of angles in degrees that need to be converted to radians. It is important to understand how to convert between degrees and radians, as they are two commonly used units of angular measurement.
Conversion Values:
| Degrees | Radians |
|---|---|
| 0° | 0 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
Note: The above conversion values are for common angles and may vary depending on the specific context or problem. It is always important to double-check the conversion values or use a calculator when converting between degrees and radians.
Converting between degrees and radians is a fundamental skill in trigonometry and calculus. Radians are often preferred in mathematical calculations due to their direct relationship with the unit circle and the use of radians in trigonometric functions. Understanding the relationship and being able to convert between these units is essential for solving problems involving angles and trigonometric functions.
Converting Radians to Degrees
The conversion between radians and degrees is an important skill in trigonometry. Radians are a unit of measurement for angles that are widely used in mathematics and physics. They provide a way to measure angles based on the radius of a circle.
To convert radians to degrees, you can use the formula: degrees = radians * (180 / π). This formula converts the radian measure into degrees by multiplying it by the conversion factor of 180 divided by π (approximately 3.14159).
Example:
- Let’s say we have an angle measure of 2 radians.
- To convert it to degrees, we can use the formula: degrees = 2 * (180 / π).
- Calculating this, we get degrees ≈ 114.59.
- Therefore, 2 radians is approximately equal to 114.59 degrees.
It is important to note that radians are the preferred unit of measurement in many mathematical calculations, as they offer more precise representations of angles. However, degrees are still widely used in everyday life and many practical applications.
Converting radians to degrees allows us to communicate angle measurements in a way that is more familiar and intuitive to most people. This conversion is particularly useful when working with trigonometric functions or when comparing angle measurements with other systems that use degrees.
Practice Questions: Converting Radians to Degrees
Below are a few practice questions to help you practice converting radians to degrees. Remember that there are 360 degrees in a circle and 2π radians in a circle.
Question 1:
Convert π/3 radians to degrees.
Answer:
To convert radians to degrees, we multiply by 180/π. Therefore, π/3 radians is equal to (π/3) * (180/π) = 60 degrees.
Question 2:
Convert 5π/4 radians to degrees.
Answer:
To convert radians to degrees, we multiply by 180/π. Therefore, 5π/4 radians is equal to (5π/4) * (180/π) = 225 degrees.
Question 3:
Convert 3π/2 radians to degrees.
Answer:
To convert radians to degrees, we multiply by 180/π. Therefore, 3π/2 radians is equal to (3π/2) * (180/π) = 270 degrees.
Question 4:
Convert 7π/6 radians to degrees.
Answer:
To convert radians to degrees, we multiply by 180/π. Therefore, 7π/6 radians is equal to (7π/6) * (180/π) = 210 degrees.
These practice questions should help you get comfortable with converting radians to degrees. Remember to use the formula: degrees = radians * (180/π).
Answer Key: Converting Radians to Degrees
In the topic of degrees and radians conversion, understanding how to convert radians to degrees is an essential skill. The answer key provides a detailed breakdown of the steps involved in converting radians to degrees, ensuring that students can practice and verify their calculations. By following these steps, students can accurately convert radians to degrees and strengthen their understanding of both angular measurements.
Step 1: Identify the given angle in radians.
Before beginning the conversion process, it is crucial to identify the angle that needs to be converted from radians to degrees. This angle will be given in radians and serves as the starting point for the conversion.
Step 2: Use the conversion formula.
The conversion formula for converting radians to degrees is to multiply the angle in radians by 180 and divide the result by pi. This formula allows for an accurate conversion between the two angular measurements.
Step 3: Apply the formula and calculate the conversion.
Using the identified angle in radians, apply the conversion formula by multiplying the angle by 180 and dividing the result by pi. This calculation will yield the equivalent angle in degrees.
Step 4: Round the result, if necessary.
Depending on the context or the specific requirements of the problem, it may be necessary to round the result of the conversion to a certain number of decimal places. This step ensures that the final answer is presented in a clear and concise manner.
By following these steps and practicing with various examples, students can become proficient in converting radians to degrees. This skill is vital in many fields, such as mathematics, physics, and engineering, where angles are commonly measured in radians and degrees. Conducting consistent and accurate conversions will enhance students’ problem-solving abilities and enable them to work effectively with both radians and degrees in various contexts.