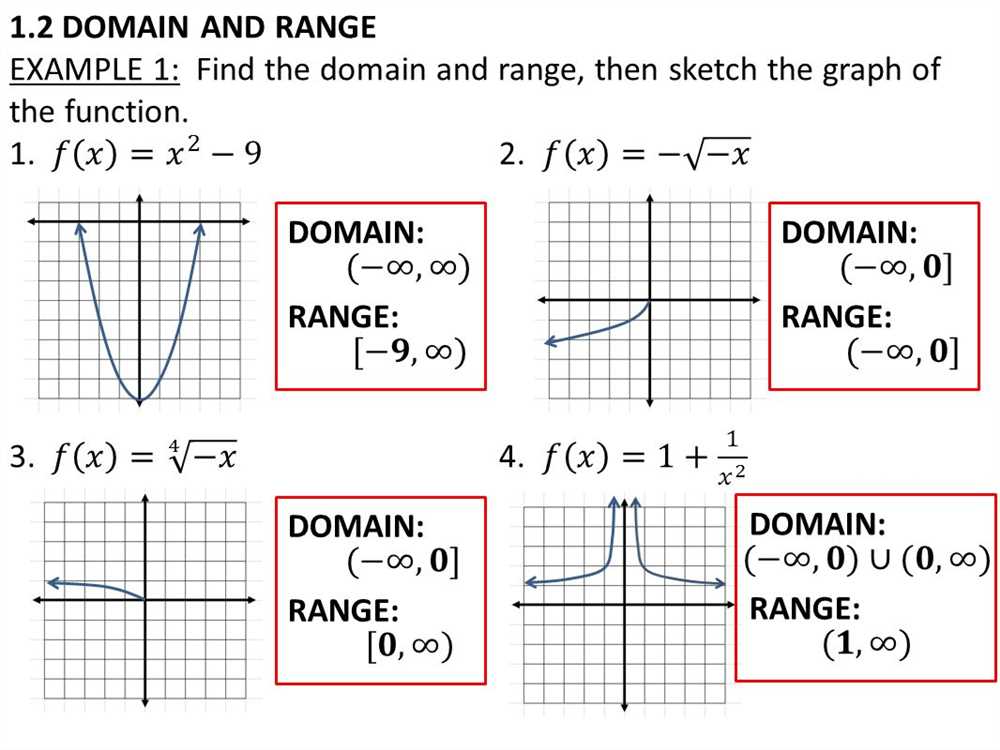
Understanding the concept of domain and range is essential for mastering functions in mathematics. In this article, we will be providing answers to a selection of questions from Domain and Range Worksheet 1. By exploring these answers, you will gain a deeper understanding of how to determine the domain and range of a given function.
Question 1: Find the domain and range of the function f(x) = 3x + 2. The domain represents the set of possible input values for the function, while the range represents the set of possible output values.
Answer: The domain of the function is all real numbers since there are no restrictions on the input value, x. The range of the function is also all real numbers, as the output value, f(x), can take on any possible real number. Therefore, the domain is (-∞, +∞) and the range is (-∞, +∞).
Question 2: Determine the domain and range of the function g(x) = √(x-4). Again, keep in mind that the domain refers to the possible input values, while the range refers to the possible output values.
Answer: The domain of g(x) is all real numbers greater than or equal to 4 since the square root function is defined for non-negative real numbers. The range of g(x) is all real numbers greater than or equal to 0. Therefore, the domain is [4, +∞) and the range is [0, +∞).
By working through these examples, you can develop a solid understanding of how to determine the domain and range of various functions. Remember, the domain and range are fundamental concepts in mathematics that allow us to analyze and describe the behavior of functions in a precise and meaningful way.
What is a domain and range?
A domain is the set of all possible input values for a function or relation. In other words, it is the set of values for which the function or relation is defined. The domain is often represented as the x-values in a function or relation and can be written as a set of numbers, inequalities, or intervals.
For example, in the function f(x) = 3x + 2, the domain would be all real numbers because the function is defined for any value of x. However, in the function g(x) = 1/x, the domain would be all real numbers except for x = 0 because the function is undefined at x = 0.
The range, on the other hand, is the set of all possible output values for a function or relation. It represents the set of values that the function or relation can produce based on its input. The range is often represented as the y-values in a function or relation and can also be written as a set of numbers, inequalities, or intervals.
Continuing with the previous examples, the range for f(x) = 3x + 2 would be all real numbers because the function can produce any real number as an output. However, the range for g(x) = 1/x would be all real numbers except for y = 0 because the function cannot produce the output of 0.
In conclusion, the domain and range are important concepts in mathematics that define the input and output values of a function or relation. They help us understand the limitations and possibilities of a function or relation and allow us to analyze its behavior and characteristics.
Why is it important to understand domain and range?
Understanding domain and range is crucial in various fields such as mathematics, physics, and computer science. Domain and range provide valuable information about the inputs and outputs of a function or relation. They help us determine the set of possible values for an independent variable and the corresponding set of values for a dependent variable.
In mathematics and physics, domain and range help us define the scope and limitations of a function or relation. They allow us to identify the set of valid inputs and outputs, which helps in solving equations, graphing functions, and understanding the behavior of mathematical models. For example, in calculus, knowledge of domain and range is essential for determining the intervals of convergence or divergence of a series or sequence.
In computer science and data analysis, domain and range are crucial for data validation and error detection. By understanding the domain and range of a function or relation, we can identify possible outliers, inconsistencies, or errors in the data. This is especially important when working with large datasets or when developing algorithms for data analysis.
In addition, understanding domain and range can help us make informed decisions and predictions. By knowing the range of a function, for example, we can determine the maximum or minimum value it can reach. This information is valuable in optimization problems, decision-making processes, and simulations.
In conclusion, understanding domain and range is essential for various disciplines. It allows us to define the scope and limitations of functions or relations, validate data, and make informed decisions. Enhancing our knowledge of domain and range enhances our understanding of mathematical models, scientific phenomena, and real-world applications.
The Basics of Domain and Range
When studying functions in mathematics, it is important to understand the concepts of domain and range. The domain of a function refers to the set of all possible input values, while the range refers to the set of all possible output values.
Domain and range can be thought of in terms of a function as a machine. The domain represents the “input” that the machine can accept, while the range represents the “output” or result that the machine produces. For example, if we have a function that takes a number as input and squares it, the domain would be all real numbers and the range would be all non-negative real numbers.
When determining the domain and range of a function, it is important to consider any restrictions or limitations that may be present. For example, if we have a function that calculates the square root of a number, the domain would be all non-negative real numbers since we cannot take the square root of a negative number. Similarly, if we have a function that represents the height of a projectile, the range would be all positive real numbers since the object cannot have a negative height.
It is also important to note that the domain and range of a function can be expressed in different ways. For example, the domain could be expressed as an interval, such as [-∞, ∞], or as a set of specific numbers. The range can also be expressed in various ways, such as a set of numbers or as an interval. Finally, in some cases, the domain or range may be limited or infinite, depending on the function and its properties.
Summary:
- The domain of a function refers to the set of all possible input values.
- The range of a function refers to the set of all possible output values.
- Domain and range can be thought of as the “input” and “output” of a function.
- Restrictions or limitations may affect the domain and range of a function.
- The domain and range can be expressed in different ways, such as intervals or sets of numbers.
Defining the Domain
When working with mathematical functions, it is important to understand the concept of domain. The domain of a function refers to the set of all possible input values or x-values for which the function is defined. In simpler terms, it is the set of values that can be plugged into the function to obtain a valid output.
For example, consider a simple function like f(x) = x^2. In this case, the domain would include all real numbers because any real number can be squared to obtain a valid output. However, if we had a function like g(x) = 1/x, the domain would be all real numbers except for x = 0, because division by zero is undefined.
The domain can also be restricted by other mathematical restrictions or physical limitations. For example, if we have a function that represents the height of a tree as it grows over time, the domain would be limited to positive values only, as negative values of time would not make sense in this context.
In some cases, the domain may need to be explicitly stated or clarified, especially when dealing with composite functions or functions with specific conditions. Sometimes, the domain may be given as a specific interval, a set of numbers, or a combination of multiple sets.
Understanding and properly defining the domain of a function is crucial for accurately analyzing and solving mathematical problems. It helps ensure that our calculations are valid and meaningful, and allows us to determine the range of valid outputs that can be obtained from a given function.
Defining the range
When solving mathematical equations or working with functions, it is important to understand the concept of the range. The range refers to the set of all possible output values of a function or equation. In other words, it is the collection of all values that the dependent variable can take on.
To define the range of a function, you need to determine the possible values that the output can be. This can be done by evaluating the function at different input values or by analyzing the equation itself. For example, if you have the equation y = 2x + 3, the range would be all real numbers, as there are no restrictions on the possible output values.
However, not all functions have an unlimited range. Some functions may have specific restrictions or limitations on the output values. For instance, if you have the equation y = x^2, the range would be all non-negative real numbers, as the square of any real number is always non-negative.
It is also possible for a function to have a finite range, which means that there is a specific range of values that the output can be. For example, if you have the equation y = sin(x), the range would be between -1 and 1, as the sine function fluctuates between these values for any input.
In summary, the range of a function is the collection of all possible output values. It can be unlimited, have specific restrictions, or be finite, depending on the function or equation. Understanding the range is crucial for understanding the behavior and characteristics of a mathematical function.
Graphing Functions
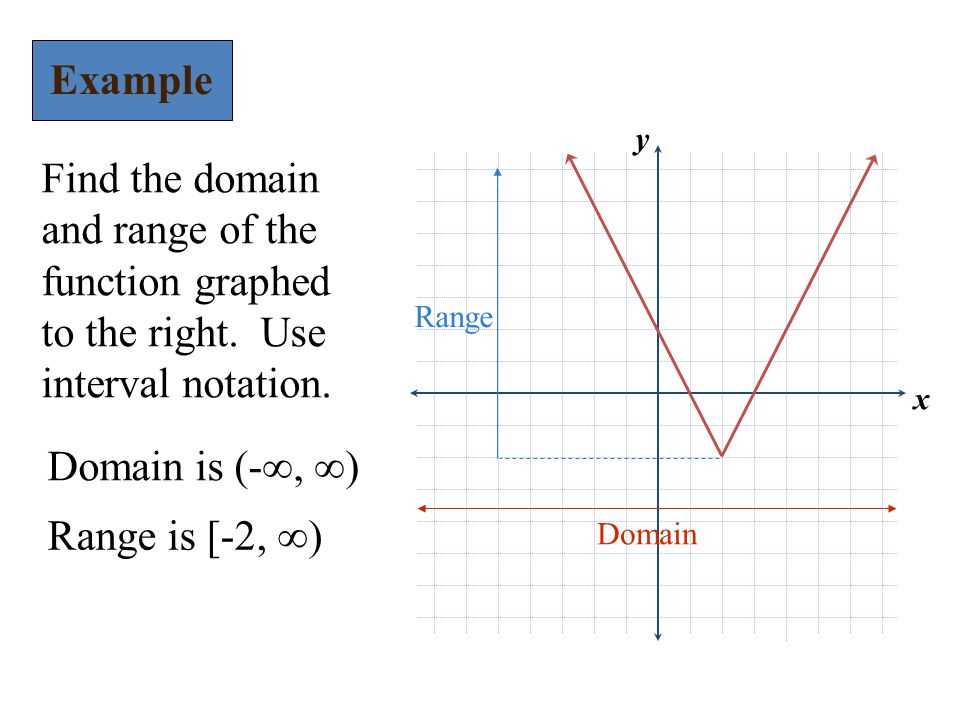
Graphing functions is a fundamental skill in mathematics that involves representing equations or mathematical relationships visually. By plotting points on a coordinate plane, we can create a graph that helps us understand and analyze the behavior of functions.
When graphing functions, it’s important to understand the concepts of domain and range. The domain of a function refers to all possible input values or x-values, while the range represents the corresponding output values or y-values. By identifying the domain and range, we can accurately plot the graph and interpret its meaning.
To graph a function, start by identifying key points by evaluating the function for specific values of x. These points can be plotted on the coordinate plane. Then, connect the points to create a smooth curve or line that represents the function’s behavior.
- For linear functions, the graph will be a straight line.
- Quadratic functions will have a parabolic shape.
- Exponential functions will show exponential growth or decay.
It’s important to pay attention to the scale of the axes when graphing functions. The intervals between the values on the axes should be consistent to accurately represent the relationship between the x and y variables. Additionally, labeling the axes and providing a title for the graph can enhance its clarity and understanding.
Overall, graphing functions is a valuable tool that allows us to visualize mathematical relationships and analyze their behavior. By mastering this skill, we can gain deeper insights into the properties and characteristics of various functions.
Understanding the graph of a function
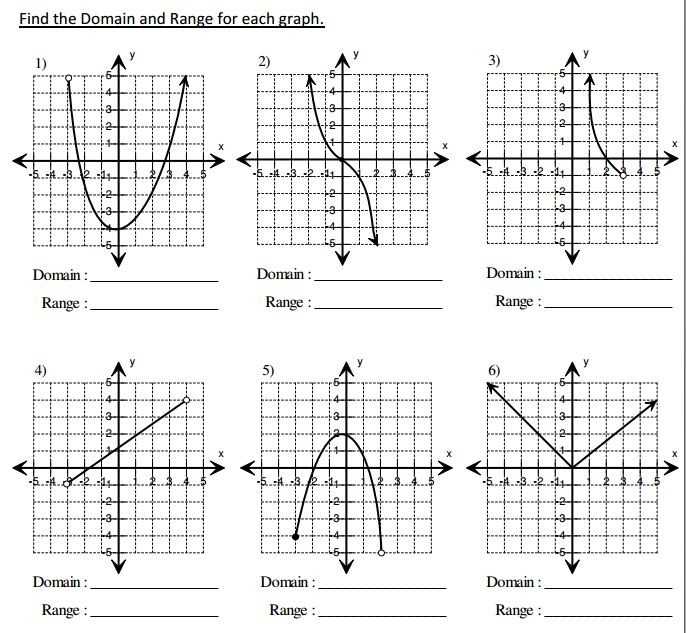
The graph of a function is a visual representation that helps us understand the relationship between the inputs and outputs of the function. It provides valuable information about the domain, range, and behavior of the function. By analyzing the graph, we can determine the values that the function can take on and the values it cannot.
When we look at a graph, we can identify the domain of the function by examining the x-values that are included in the graph. The domain is the set of all possible inputs for the function. Similarly, the range of the function can be determined by looking at the y-values that are included in the graph. The range is the set of all possible outputs of the function.
The graph of a function can also provide insights into its behavior. For example, we can identify whether the function is increasing or decreasing by examining the direction of the graph. A function is increasing if its graph moves upwards as we move from left to right, and it is decreasing if its graph moves downwards. Additionally, we can determine the maximum and minimum values of the function by identifying the highest and lowest points on the graph.
By understanding the graph of a function, we can make informed decisions about its properties and make predictions about its behavior. It allows us to see patterns, identify important points, and analyze how the function changes with different inputs. Whether it is a linear, quadratic, exponential, or any other type of function, the graph provides us with a visual representation that aids our understanding.
Identifying the domain and range from a graph
When analyzing a graph, it is important to identify the domain and range of the function represented by the graph. The domain represents the set of all possible input values for the function, while the range represents the set of all possible output values.
To determine the domain of a function from a graph, we look at the x-values that are included in the graph. If there are no restrictions or gaps in the graph, the domain is typically all real numbers. However, if there are restrictions or gaps, we must determine the specific range of x-values that are included in the graph.
On the other hand, to determine the range of a function from a graph, we examine the y-values that are included in the graph. We look for the highest and lowest points on the graph to determine the range. If the graph extends infinitely in the positive and negative directions, the range is typically all real numbers. However, if the graph is bounded or has an upper or lower limit, the range will be restricted to a specific set of values.
It is important to carefully analyze the graph and consider any restrictions or gaps that may exist in order to accurately determine the domain and range. By understanding the domain and range of a function, we can better understand the behavior of the function and make predictions about its values.