
Equations are fundamental in mathematics as they allow us to express relationships between variables and find unknown values. Solving equations can be a challenging task, but with the Equation Ornaments Problem Set C and its answer key, you can gain a comprehensive understanding of the various techniques and strategies used to solve equations.
This answer key provides detailed explanations and step-by-step solutions to each problem in the Equation Ornaments Problem Set C. It covers a wide range of equation types, including linear, quadratic, exponential, and logarithmic equations. By studying these solutions, you will learn how to apply different methods such as factoring, completing the square, and using the quadratic formula to solve equations.
Whether you are a student looking to improve your equation-solving skills or a teacher seeking additional resources for your classroom, the Equation Ornaments Problem Set C Answer Key is a valuable tool. It offers a comprehensive review of equation-solving techniques and provides ample practice to reinforce your understanding of these concepts.
With the Equation Ornaments Problem Set C Answer Key, you can confidently tackle any equation and become proficient in solving even the most complex mathematical problems. So, grab a copy of the answer key and embark on a journey to master equation-solving skills!
Equation Ornaments Problem Set C Answer Key
In the equation ornaments problem set C, students are tasked with solving equations to find the value of the variable in order to decorate the Christmas ornaments. The answer key provides the correct solutions to these equations, allowing students to check their work and ensure accuracy in their calculations.
The problem set C answer key lists the equations along with the correct value for the variable. This allows students to compare their own answers and see if they have correctly solved the equations. The answer key also provides explanations and step-by-step solutions for each equation, helping students understand the reasoning behind the correct answers.
By using the equation ornaments problem set C answer key, students can assess their understanding of solving equations and identify any areas where they may need additional practice. It serves as a valuable tool for reinforcing mathematical concepts and building confidence in problem-solving skills.
Example Answer Key:
- Equation 1: 3x + 5 = 20
- Variable value: x = 5
- Step-by-step solution: Subtract 5 from both sides, then divide by 3.
- Equation 2: 2(4x – 3) = 14
- Variable value: x = 8
- Step-by-step solution: Expand the brackets, then divide by 2.
- Equation 3: 7x – 10 = 24
- Variable value: x = 6
- Step-by-step solution: Add 10 to both sides, then divide by 7.
With the equation ornaments problem set C answer key, students can confidently solve equations and decorate their Christmas ornaments with the correct values.
Problem C1: Solve for x
In this problem, we are given an equation involving x and other variables. Our task is to solve for x and find its value.
The given equation is:
3x – 4 = 7
To solve for x, we need to isolate it on one side of the equation. In this case, we can start by adding 4 to both sides of the equation to eliminate the constant term -4:
3x – 4 + 4 = 7 + 4
This simplifies to:
3x = 11
Next, we divide both sides of the equation by the coefficient of x, which is 3:
(3x) / 3 = 11 / 3
Therefore, the solution to the equation is:
x = 11 / 3
In decimal form, this is approximately:
x ≈ 3.6667
So, the value of x that satisfies the equation is approximately 3.6667.
Problem C2: Graphing Linear Equations
In this problem, we are given a set of linear equations and we need to graph them on a coordinate plane. Graphing linear equations helps us visualize the relationship between two variables and understand how they interact.
To graph a linear equation, we first need to identify the slope and y-intercept of the equation. The slope is the rate of change of the line, and the y-intercept is the point where the line crosses the y-axis. These two pieces of information help us determine the position of the line on the coordinate plane.
Once we have identified the slope and y-intercept, we can plot the y-intercept on the y-axis and use the slope to find additional points on the line. We can do this by starting at the y-intercept and moving up or down based on the slope. For example, if the slope is positive, we move up for each unit increase in x, and if the slope is negative, we move down for each unit increase in x.
After plotting several points, we can connect them using a straight line to represent the linear equation on the graph. This line represents all the possible solutions to the equation and helps us understand the relationship between the variables.
In conclusion, graphing linear equations allows us to visually represent the relationship between two variables. It helps us understand the slope and y-intercept of the equation and allows us to identify the points on the line. By connecting these points, we can represent the linear equation on a graph and analyze its behavior and solution set.
Problem C3: Systems of Equations
In problem C3, we are presented with a system of equations and tasked with finding the solution. A system of equations consists of multiple equations that need to be solved simultaneously, where the solution is the set of values that satisfy all the equations.
The problem provides two equations, usually in the form of linear equations with two variables. We need to find the values of the variables that make both equations true. This can be done through various methods, such as substitution or elimination.
For example, let’s consider the following system of equations:
- Equation 1: 2x + 3y = 10
- Equation 2: 4x – 2y = 4
To solve this system, we can use the method of substitution. From Equation 1, we can isolate one variable, for example, x:
2x + 3y = 10 (Equation 1)
2x = 10 – 3y
x = (10 – 3y)/2
Now we can substitute this expression for x into Equation 2:
4((10 – 3y)/2) – 2y = 4 (Equation 2)
Simplifying further, we can solve for y:
20 – 6y – 2y = 4
-8y = -16
y = 2
Substituting this value back into the expression for x, we can find x:
x = (10 – 3(2))/2 = 1
Therefore, the solution to the system of equations is x = 1, y = 2.
Problem C4: Quadratic Equations
In this problem, we are given a set of quadratic equations and asked to solve for their roots. Quadratic equations are equations of the form ax² + bx + c = 0, where a, b, and c are constants.
For each quadratic equation in the problem set, we can use the quadratic formula to find the roots. The quadratic formula states that the roots of a quadratic equation can be found using the formula:
x = (-b ± √(b²-4ac))/2a
To solve each equation, we substitute the given values of a, b, and c into the quadratic formula, and then solve for x. If the discriminant (b²-4ac) is positive, we will have two real roots. If the discriminant is zero, we will have one real root. If the discriminant is negative, we will have two complex roots.
It is important to pay attention to the signs and the order of operations when performing calculations. Additionally, it is always a good idea to check our solutions by substituting the found values back into the original equation to ensure they satisfy the equation.
By solving the given quadratic equations, we can find the roots and gain a better understanding of the behavior of quadratic functions.
Problem C5: Exponential Equations
In problem C5, we are presented with exponential equations to solve. Exponential equations involve variables in the exponent, and the goal is to find the value of the variable that satisfies the equation. In this problem set, we will practice solving these types of equations. Let’s take a look at an example:
Example:
Solve the equation 3x = 81.
In this example, we have to find the value of x that satisfies the equation. To solve exponential equations like this, we can take the logarithm of both sides. Applying the logarithm to the equation, we get:
- log(3x) = log(81)
- x * log(3) = log(81)
- x = log(81) / log(3)
After evaluating the logarithm expressions and dividing, we find that x = 4. Therefore, the solution to the equation 3x = 81 is x = 4.
In problem set C5, we will be given similar exponential equations to solve. It is important to remember the properties of logarithms and how to apply them to solve these equations. Practice is key to mastering this skill, so let’s proceed to the problem set and solve some exponential equations!
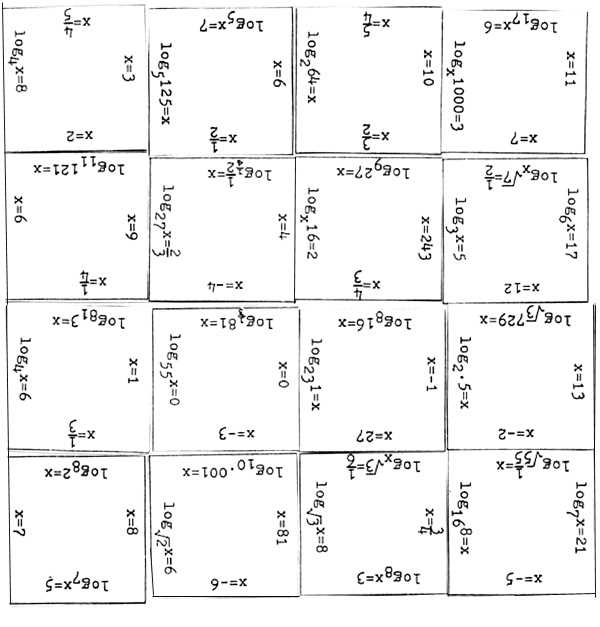
Problem C6: Logarithmic Equations
In problem C6, we will be working with logarithmic equations. Logarithmic equations involve the use of logarithmic functions to solve for unknown variables or values. These equations can be quite complex and require a good understanding of logarithmic properties and rules.
One important property of logarithms is the power rule. The power rule states that for any positive numbers a, b, and c, if loga(b) = c, then ac = b. This property allows us to rewrite logarithmic equations in exponential form and solve for the variable using basic algebraic techniques.
Let’s take an example logarithmic equation: log2(x+3) = 4. To solve for x in this equation, we can apply the power rule and rewrite the equation in exponential form: 24 = x+3. Simplifying this equation, we get 16 = x+3. Thus, x = 13.
Logarithmic equations can also involve more than one logarithmic term. In such cases, we may need to use logarithmic properties like the product rule or the quotient rule to simplify the equation and isolate the variable. It is important to carefully apply these properties and rules to ensure accurate solutions to logarithmic equations.
Overall, logarithmic equations can be challenging but rewarding to solve. They require a solid understanding of logarithmic properties and rules, as well as proficiency in basic algebraic techniques. By applying these concepts and techniques, we can successfully solve logarithmic equations and find the values of unknown variables.
Problem C7: Polynomial Equations
In this problem, we are given a polynomial equation and we need to find the value(s) of the variable that satisfy the equation. A polynomial equation consists of multiple terms involving addition, subtraction, multiplication, and exponentiation of a variable. The power of the variable in each term is always a whole number (non-negative integer).
To solve a polynomial equation, we need to rearrange the terms so that all the terms are on one side of the equation and the other side is equal to zero. This form is called the standard form of a polynomial equation. Once we have the equation in standard form, we can use various methods to find the value(s) of the variable that satisfy the equation.
One method to solve a polynomial equation is by factoring. By factoring the polynomial equation, we can express it as a product of two or more polynomials. This allows us to set each factor equal to zero and solve for the variable. Another method is by using the quadratic formula, which is used specifically for solving quadratic equations (polynomial equations of degree 2).
In some cases, polynomial equations may have multiple solutions, while in other cases, there may be no solution. It is also possible for a polynomial equation to have only one solution. To determine the number of solutions, we can analyze the degree of the polynomial equation and the nature of its terms.
Overall, solving polynomial equations requires understanding the properties of polynomials and applying various methods and techniques to find the values of the variable that satisfy the equation. It is an important topic in algebra and has applications in various fields of science and engineering.
Problem C8: Radical Equations
Problem:
The equation ornaments set C contains several problems that involve solving radical equations. These equations involve radicals, such as square roots or cube roots, and they require finding the values of the variable that make the equation true. The solutions to these equations can be real numbers, but they may also involve imaginary numbers.
Solution:
To solve radical equations, it is often necessary to isolate the radical term by itself on one side of the equation. This can be done by applying inverse operations, such as squaring both sides of the equation if the radical term is a square root. However, it is important to check for extraneous solutions, as squaring both sides can introduce additional solutions that do not satisfy the original equation.
For example, consider the equation √(2x+1) = 3. To isolate the radical term, square both sides of the equation: (√(2x+1))^2 = 3^2. This simplifies to 2x+1 = 9. Solving for x, we get x = 4. However, it is necessary to check this solution by substituting it back into the original equation: √(2(4)+1) = 3. This simplifies to √9 = 3, which is true. Therefore, x = 4 is a valid solution.
- Other problems in set C may involve different types of radicals or require additional algebraic manipulations. It is important to carefully follow the steps and check solutions to ensure accuracy.
- The equation ornaments set C also includes problems that require solving systems of radical equations, where multiple equations with radicals need to be solved simultaneously. This can be done by eliminating one variable at a time using substitution or elimination methods.
- Remember to always check solutions by substituting them back into the original equation to verify their validity. Additionally, be mindful of any restrictions on the variable that may arise from the domain of the radical.
- By practicing and mastering the skills involved in solving radical equations, you will be well-prepared to tackle more challenging problems in algebra and beyond.