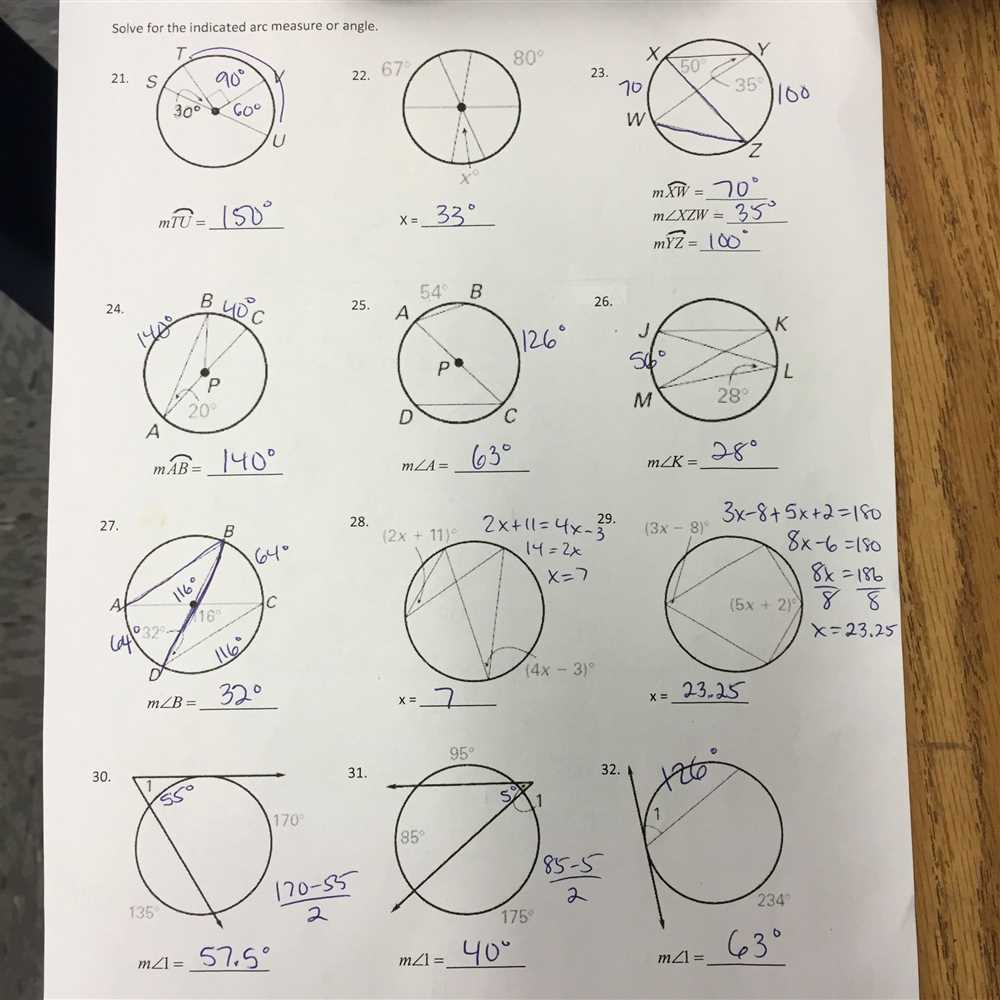
In geometry, the equations of circles play a fundamental role in understanding the properties and characteristics of these fundamental shapes. Circles are among the most basic and recognizable shapes, and their equations can reveal valuable insights into their location, size, and relationship with other geometric objects. The “Equations of Circles Coloring Activity” is a fun and interactive way for students to practice solving and graphing equations of circles, and this answer key provides the solutions for the activity.
The activity involves a series of equations of circles, each with different centers and radii. Students are required to solve the equations and graph the corresponding circles. By correctly solving the equations, they will determine the center and radius of each circle and accurately plot them on the coordinate plane. This coloring activity not only allows students to practice their equation solving skills but also helps them visualize the geometric nature of circles.
The answer key for the “Equations of Circles Coloring Activity” provides students with the correct solutions and graphing instructions for each equation. It serves as a valuable resource for teachers, ensuring that students have access to accurate answers and helping them check their work. By comparing their own solutions with the answer key, students can identify any errors or misconceptions and further improve their understanding of equations of circles.
Overview

In the study of geometry, circles play an important role. They are a simple and elegant shape that can be found in nature and used in many practical applications. Understanding the equations of circles is a fundamental concept in geometry and can help us solve various problems.
This coloring activity on equations of circles is designed to help students practice identifying the center and radius of a circle based on its equation. The activity includes a set of equations, and students need to determine the center and radius of each circle and color them accordingly. This hands-on activity engages students in a fun and interactive way, making it easier for them to grasp the concept.
The answer key for the coloring activity provides the correct solutions for each equation, allowing students to check their work and assess their understanding. It serves as a valuable resource for both students and teachers, ensuring accuracy and providing feedback on their progress.
How to use the answer key:
- Students can compare their answers with the ones provided in the answer key to see if they have correctly identified the center and radius of each circle.
- If there are any discrepancies, students can review their work and make necessary corrections.
- The answer key can also be used as a reference for students who are struggling to solve certain equations. They can examine the correct solutions and understand the steps involved in determining the center and radius.
- Teachers can use the answer key to assess the students’ understanding and identify any areas that need further clarification or additional practice.
Overall, this coloring activity and its answer key provide an engaging and effective way for students to practice and master the concepts of equations of circles. By combining hands-on learning with immediate feedback, students can develop a solid foundation in geometry and enhance their problem-solving skills.
Explanation of the Activity
The activity “Equations of circles coloring” is a fun and engaging way for students to practice solving equations of circles. It is designed for students who are learning about circles and their equations in geometry. This activity allows students to apply their knowledge of equations of circles in a visual and interactive way.
The activity consists of a worksheet with several equations of circles written in standard form. Each equation represents a different circle. The students are required to solve each equation and identify the center and radius of the corresponding circle. Once they have solved the equation and found the center and radius, they can color the circle on the worksheet.
The coloring activity not only reinforces the concept of equations of circles but also allows students to see the different shapes and sizes of circles that can be formed. It helps them develop a better understanding of the relationship between the equation and the properties of a circle. The coloring aspect also adds an element of creativity to the activity, making it more enjoyable for the students.
This activity can be done individually or in small groups. It can be used as an in-class activity or as homework to reinforce the concept of equations of circles. The answer key is provided to check for accuracy and to provide feedback to the students. Overall, the “Equations of circles coloring” activity is an effective tool for practicing and reinforcing the concept of equations of circles in geometry.
Importance of understanding equations of circles

Understanding equations of circles is essential in various fields of study, such as mathematics, physics, engineering, and computer science. Equations of circles allow us to describe and analyze the properties of circles, which are fundamental geometric shapes.
In mathematics, equations of circles are an important topic in geometry. They help us understand the relationship between the geometric properties of circles, such as their radius, diameter, and center, and the coordinates of their points. This knowledge is crucial when working with circles in higher-level mathematical concepts, such as coordinate geometry and calculus.
In physics, equations of circles are used to describe the motion of objects in circular paths, such as planets orbiting the sun or satellites orbiting the Earth. By understanding these equations, physicists can determine the speed, acceleration, and other characteristics of objects moving in circular trajectories.
In engineering, equations of circles are applied in various fields, including structural engineering, mechanical engineering, and electrical engineering. Engineers use these equations to design and analyze circular structures, such as bridges, gears, and electrical circuits. The understanding of equations of circles is crucial for ensuring the stability, functionality, and efficiency of these engineered systems.
In computer science, equations of circles are used in computer graphics and image processing. They are employed to generate and manipulate circular shapes in computer-generated images and animations. Understanding equations of circles enables computer scientists to create realistic and visually appealing circular objects in virtual environments.
In summary, understanding equations of circles is of utmost importance in various fields of study. Mastering these equations allows us to describe, analyze, and manipulate circles, leading to advancements in mathematics, physics, engineering, computer science, and many other areas of knowledge.
Benefits of using coloring activities for learning
Coloring activities can be an effective and engaging way for students to learn and reinforce their understanding of complex concepts, such as equations of circles. By incorporating colors and creativity into the learning process, students are more likely to stay motivated and actively participate in the activity.
One of the main benefits of using coloring activities is that they promote active learning. Instead of passively reading or listening to information, students are actively engaged in the task of coloring, which requires them to analyze and make decisions based on their understanding of the topic. This hands-on approach helps students to better comprehend and remember the material.
Visual stimulation: Coloring activities provide visual stimulation, which can help improve concentration and focus. When students are engaged in coloring intricate designs or patterns, it activates different areas of the brain and enhances their cognitive abilities.
Artistic expression: Coloring activities allow students to express their creativity and individuality. They can choose different colors and techniques to complete the activity, which gives them a sense of ownership and pride in their work. This can boost their confidence and encourage them to take an active role in their own learning.
Collaborative learning: Coloring activities can also be done in groups, promoting collaboration and teamwork among students. This not only helps students to develop their social skills, but also allows them to learn from each other and exchange ideas and strategies.
Relaxation and stress relief: Coloring has been shown to have a calming effect on the mind and body, making it an excellent tool for relaxation and stress relief. By incorporating coloring activities into the learning process, students can experience a sense of calmness and reduce any anxiety or stress they may be feeling.
In conclusion, coloring activities can be a valuable addition to the learning process. They provide visual stimulation, encourage artistic expression, promote collaboration, and offer relaxation benefits. By incorporating these activities into the classroom, educators can create a more engaging and effective learning environment for their students.
Step-by-step guide to solving equations of circles
When solving equations of circles, it is important to follow a systematic approach to ensure accuracy and efficiency. Here is a step-by-step guide to help you tackle these types of equations:
Step 1: Understand the equation

The equation of a circle is typically written in the form (x – h)^2 + (y – k)^2 = r^2, where (h, k) represents the center of the circle and r represents its radius. Take a moment to identify these values in the given equation and understand their significance.
Step 2: Determine the center and radius
In order to solve the equation, you need to determine the values of (h, k) and r. Use algebraic methods such as completing the square or factoring to rearrange the equation into the standard form. From there, you can easily identify the center and radius.
Step 3: Graph the circle
Once you have determined the center and radius, plot these points on a coordinate plane. Use a ruler or compass to draw the circle with the appropriate radius centered at the given point.
Step 4: Check your work
After solving the equation and graphing the circle, it is important to double-check your work. Make sure the equation is in standard form, the center and radius are correct, and the graph accurately represents the given equation.
By following these steps, you can confidently solve equations of circles and accurately represent them on a graph. Practice with a variety of equations to strengthen your skills in this area.
Color Key for the Activity
In this activity, students are given a set of equations of circles and they have to find the corresponding color for each equation. The color key helps them determine which color to fill in for each equation. Below is the color key for this activity:
- Equation of a circle: The equation of the form (x – h)^2 + (y – k)^2 = r^2 represents a circle. The coordinates (h, k) represent the center of the circle, and r represents the radius.
- Center of the circle: The center of the circle can be determined by identifying the values of h and k in the equation.
- Radius of the circle: The radius of the circle can be determined by finding the square root of r^2 in the equation.
- Solving for y: To find the equation in the form y = mx + c, students need to solve the equation by isolating y on one side.
- Intercept: The intercept can be found by setting x or y to zero and solving for the other variable.
By using this color key, students will be able to identify the key components of each equation of a circle and determine the correct color to fill in for each equation. This activity helps reinforce students’ understanding of the equation of a circle and allows them to practice solving for y and finding intercepts. It also provides an engaging and interactive way for students to practice their coloring skills while learning about circles.
Common mistakes to avoid when solving equations of circles
When solving equations of circles, there are several common mistakes that students should be aware of in order to avoid errors and ensure accurate solutions. One common mistake is misinterpreting the equation of a circle. The equation of a circle is in the form (x-h)^2 + (y-k)^2 = r^2, where (h,k) represents the center of the circle and r represents the radius. Students sometimes incorrectly identify the terms in the equation, leading to inaccurate solutions.
Another mistake to avoid is forgetting to square both the x and y terms in the equation. Since the equation of a circle involves squaring the distances from the center, it is essential to remember to square both the x and y terms. Failure to do so will result in an incorrect solution.
Additionally, students may mistakenly mix up the signs of the terms in the equation. For example, if the equation is (x-3)^2 + (y+2)^2 = 9, some students may incorrectly write it as (x+3)^2 + (y-2)^2 = 9. Mixing up the signs in the equation will lead to a different circle and an incorrect solution.
It is also important to be attentive to details when solving equations of circles. Small errors in calculations or signs can result in completely different solutions. Students should double-check their work and carefully follow the steps of solving the equation to avoid making mistakes.
In conclusion, when solving equations of circles, it is crucial to accurately interpret the equation and square both the x and y terms. Students should also be mindful of the signs in the equation and diligently check their work for errors. By avoiding these common mistakes, students can ensure accurate solutions to equations of circles.