
If you are studying physics and looking for practice problems to enhance your understanding of equations of motion, we have got you covered. In this article, we will provide you with a worksheet containing various equations of motion problems along with their answers in PDF format. This worksheet is designed to test your understanding of the kinematic equations and their application in real-life scenarios.
The equations of motion are fundamental to the study of physics and mechanics. They describe the relationship between an object’s displacement, velocity, acceleration, and time. By solving problems related to equations of motion, you can develop your problem-solving skills and gain a deeper understanding of how objects move in different situations.
The worksheet we are providing includes a range of problems covering different aspects of kinematics, including finding the displacement, velocity, acceleration, and time of an object. Each problem is accompanied by a detailed solution, allowing you to check your answers and understand the steps involved in solving the problem.
By working through this equations of motion worksheet, you can practice applying the kinematic equations to various scenarios and improve your problem-solving abilities. So, download the PDF file, grab a pen and paper, and get ready to dive into the world of equations of motion!
Equations of Motion Worksheet with Answers PDF

Equations of motion are mathematical formulas that describe the relationship between the displacement, velocity, acceleration, and time of an object. These equations are fundamental in physics and are used to solve problems related to the motion of objects.
A worksheet with answers in PDF format can be a helpful resource for students learning about equations of motion. It provides practice problems that allow students to apply the equations and test their understanding of the concepts. The answers included in the worksheet enable students to check their work and identify any mistakes they may have made.
The equations of motion worksheet typically includes a variety of problems involving different scenarios, such as objects moving with constant velocity, objects accelerating or decelerating, or objects experiencing free fall. Each problem presents a situation and asks students to solve for a specific variable using the appropriate equation of motion.
Using a PDF format for the worksheet allows for easy printing and distribution to students. It also ensures that the document is easily accessible on various devices, making it convenient for students to access and complete the worksheet both in the classroom and at home.
In conclusion, an equations of motion worksheet with answers in PDF format is a valuable educational tool for students studying physics. It provides them with practice problems to reinforce their understanding of the equations and allows them to check their answers for accuracy. By using this worksheet, students can improve their problem-solving skills and gain a deeper comprehension of the principles of motion.
Overview of Equations of Motion
The equations of motion are a set of mathematical equations that describe the motion of an object in terms of its position, velocity, and acceleration. These equations are derived from Newton’s laws of motion and are commonly used in physics and engineering to analyze and solve problems related to motion.
There are three main equations of motion, which are commonly referred to as the equations of uniformly accelerated motion. These equations are:
- First equation of motion: This equation relates the final velocity (v), initial velocity (u), acceleration (a), and time (t) of an object. It is expressed as v = u + at.
- Second equation of motion: This equation relates the displacement (s), initial velocity (u), acceleration (a), and time (t) of an object. It is expressed as s = ut + 0.5at^2.
- Third equation of motion: This equation relates the final velocity (v), initial velocity (u), acceleration (a), and displacement (s) of an object. It is expressed as v^2 = u^2 + 2as.
These equations allow us to calculate various parameters of an object’s motion, such as its final velocity, displacement, or time taken to reach a certain point. They are particularly useful when dealing with uniformly accelerated motion, where the acceleration remains constant throughout the object’s motion.
By applying these equations and using known values, we can solve problems involving motion, such as finding the time it takes for an object to reach a certain velocity, or determining the displacement of an object given its initial velocity and acceleration.
Importance of Equations of Motion in Physics
The equations of motion play a crucial role in the field of physics, as they provide a mathematical framework to describe the motion of objects. These equations allow us to quantitatively analyze and predict the behavior of objects as they move through space and time.
One of the key benefits of using equations of motion is the ability to accurately model and understand the motion of complex systems. By applying these equations, physicists can determine the position, velocity, and acceleration of an object at any given time. This is particularly important in fields such as astrophysics, where the motion of celestial bodies can be extremely complex and difficult to observe directly.
Furthermore, the equations of motion enable scientists to study the fundamental laws of nature and explore the underlying principles that govern how objects move. They provide a foundation for understanding concepts such as force, momentum, and energy, and allow researchers to make predictions and test hypotheses in a controlled and quantitative manner.
In addition to their scientific significance, the equations of motion have practical applications in various fields. For example, they are used in engineering to design and analyze the motion of machines and structures. They are also utilized in fields such as robotics, where the precise control of movement is essential.
In conclusion, the equations of motion are of paramount importance in physics. They provide a powerful tool for understanding and analyzing the motion of objects, and serve as a foundation for exploring the fundamental laws of nature. Their practical applications extend beyond the field of physics, making them a valuable tool in various scientific and engineering disciplines.
Derivation of Equations of Motion
The equations of motion are fundamental equations in physics that describe the motion of objects. These equations relate the displacement, velocity, and acceleration of an object with time. The derivation of the equations of motion starts with the basic definitions of displacement, velocity, and acceleration.
The first equation of motion, also known as the velocity-time equation, can be derived by considering the definition of average velocity. Average velocity is defined as the displacement divided by the time taken. By rearranging the equation, we can express displacement in terms of average velocity and time. This equation is represented as:
Displacement (s) = Average Velocity (v) × Time (t)
The second equation of motion, also known as the acceleration-time equation, can be derived from the definition of average acceleration. Average acceleration is defined as the change in velocity divided by the time taken. By rearranging the equation, we can express change in velocity in terms of average acceleration and time. This equation is represented as:
Change in Velocity (v – u) = Average Acceleration (a) × Time (t)
The third equation of motion can be derived by combining the first and second equations of motion. By substituting the expression for displacement from the first equation into the second equation, we can eliminate displacement and obtain an equation that relates initial velocity, acceleration, and time. This equation is represented as:
Final Velocity (v) = Initial Velocity (u) + Acceleration (a) × Time (t)
These equations of motion are widely used in different branches of physics to analyze and solve problems related to the motion of objects. They provide a mathematical framework for understanding and predicting the behavior of moving objects.
Types of Equations of Motion
The equations of motion are mathematical formulas that describe the motion of an object. There are different types of equations of motion, each of which is used to represent specific aspects of the motion.
1. Uniform Motion: The equation of motion for uniform motion is given by s = ut + 1/2at^2, where s represents the displacement of the object, u is the initial velocity, t is the time taken, and a is the acceleration. This equation is used when the object is moving with a constant velocity.
2. Accelerated Motion: The equation of motion for accelerated motion is given by s = ut + 1/2at^2, where the variables have the same meanings as in the equation for uniform motion. This equation is used when the object is subjected to a constant acceleration.
3. Decelerated Motion: The equation of motion for decelerated motion is the same as the equation for accelerated motion, s = ut + 1/2at^2, but with a negative acceleration. This equation is used when the object is slowing down due to a negative acceleration.
4. Free Fall: The equation of motion for an object in free fall is s = ut + 1/2gt^2, where g represents the acceleration due to gravity. This equation is used when the object is falling under the influence of gravity.
5. Projectile Motion: The equations of motion for projectile motion involve both the horizontal and vertical components of the motion. The horizontal component is given by x = uxt, where x represents the horizontal displacement, u is the initial horizontal velocity, and t is the time. The vertical component is given by y = uyt – 1/2gt^2, where y represents the vertical displacement, u is the initial vertical velocity, t is the time, and g is the acceleration due to gravity.
In summary, the equations of motion are essential tools in the study of motion. They enable us to describe and analyze different types of motion, such as uniform motion, accelerated and decelerated motion, free fall, and projectile motion.
Examples and Practice Problems
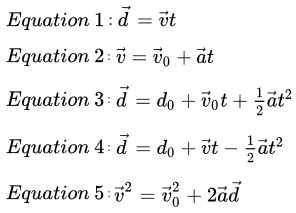
Here are some examples and practice problems to help you reinforce your understanding of the equations of motion:
Example 1:
A car is traveling at a constant velocity of 20 m/s. What is the distance it will cover in 10 seconds?
To solve this problem, we can use the equation: distance = velocity × time.
Given that the velocity is 20 m/s and the time is 10 seconds, we can substitute these values into the equation:
distance = 20 m/s × 10 s = 200 meters
Therefore, the car will cover a distance of 200 meters in 10 seconds.
Example 2:
A ball is dropped from a height of 45 meters. How long will it take for the ball to reach the ground?
To solve this problem, we can use the equation: time = √(2 × distance / acceleration).
Given that the distance is 45 meters and the acceleration due to gravity is approximately 9.8 m/s^2, we can substitute these values into the equation:
time = √(2 × 45 m / 9.8 m/s^2) = √(90 / 9.8) ≈ √9.18 ≈ 3.03 seconds
Therefore, it will take approximately 3.03 seconds for the ball to reach the ground.
These examples and practice problems will help you apply the equations of motion to different scenarios. Remember to always identify the given values and choose the appropriate equation to solve the problem. Practice until you feel confident in your understanding of the equations and their application.
Step-by-Step Solutions for Equations of Motion
In physics, equations of motion are used to describe the motion of objects. These equations can help calculate various parameters such as displacement, velocity, acceleration, and time. Solving equations of motion can be challenging, but with a step-by-step approach, it becomes easier to understand and apply the concepts.
1. Identify the known and unknown variables: Before starting to solve an equation of motion, it is important to identify the known and unknown variables. Known variables can be given in the problem statement or can be calculated from other equations. Common variables in equations of motion include displacement (s), initial velocity (u), final velocity (v), acceleration (a), and time (t).
2. Choose the appropriate equation of motion: Depending on the given information and the variable to be solved for, choose the appropriate equation of motion. There are three main equations of motion:
- Displacement: s = ut + (1/2)at²
- Final velocity: v = u + at
- Velocity squared: v² = u² + 2as
3. Plug in the known values: Substitute the known values into the chosen equation of motion. Make sure to use consistent units for all variables.
4. Rearrange and solve for the unknown variable: Rearrange the equation to solve for the unknown variable. This may involve isolating the unknown variable on one side of the equation by performing algebraic operations.
5. Substitute the values and calculate: Once the unknown variable is isolated, substitute the known values back into the equation and calculate the unknown variable. Keep in mind the units and significant figures in the final answer.
6. Check the solution: After obtaining the value for the unknown variable, double-check the solution by substituting the values back into the original equation of motion. The left side of the equation should equal the right side.
By following these step-by-step solutions for equations of motion, one can effectively solve problems related to the motion of objects. Practice and familiarity with these equations will help improve problem-solving skills in physics.
Benefits of Using a Worksheet with Answers PDF

Using a worksheet with answers in PDF format can be incredibly beneficial for students and educators alike. Here are a few key advantages of utilizing this type of resource:
1. Time-saving: The worksheet provides answers to the questions, reducing the amount of time students need to spend searching for solutions. This allows them to focus more on understanding the concepts and practicing problem-solving skills.
2. Immediate feedback: Having the answers readily available allows students to check their work immediately after completing each question. This instant feedback helps to reinforce their understanding of the material and identify any misconceptions or errors.
3. Enhanced learning experience: With a worksheet that provides answers, students can work independently and at their own pace. They can use the answers as a guide to self-assess their understanding and progress, making the learning process more personalized and engaging.
4. Effective revision tool: A worksheet with answers serves as a valuable revision tool, allowing students to review and practice a variety of problems. By referring to the answers, they can identify areas where they need to improve and focus their revision efforts accordingly.
5. Facilitates teacher planning: For educators, a worksheet with answers PDF can be a valuable resource for lesson planning. The provided answers can help teachers understand the difficulty level and content coverage of the questions, enabling them to design effective learning activities and assessments.
In conclusion, using a worksheet with answers in PDF format offers numerous benefits. It saves time, provides instant feedback, enhances the learning experience, serves as an effective revision tool, and aids in teacher planning. This type of resource can greatly support students and educators in their pursuit of academic success.