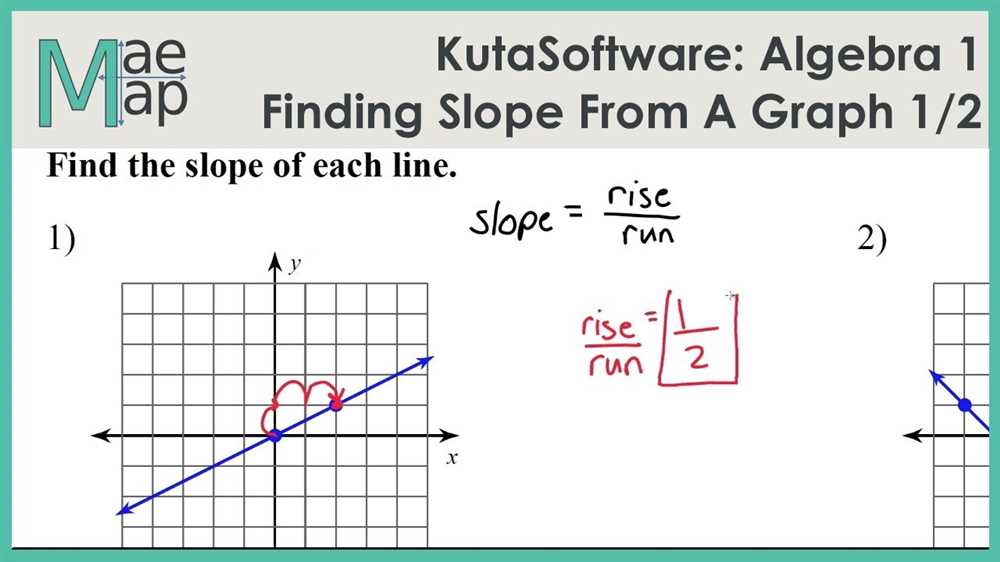
Learning about slope can be a challenging concept for students, but it doesn’t have to be boring. One engaging activity is the Finding Slope from Two Points Coloring Activity, which uses pumpkins as a theme to make it more fun and relatable. This answer key will help students check their work and understand the process of finding slope.
The activity involves a series of pumpkin-themed graphs with two points labeled on each. Students are tasked with finding the slope of the line that passes through the two points. They then match their calculated slope with the corresponding color on a key and color the pumpkin accordingly. This helps them visually see how changing slope affects the graph and reinforces their understanding of the concept.
The Answer Key provides students with the correct slope for each graph and the corresponding color. It serves as a helpful tool for self-assessment, allowing students to check their work and identify any mistakes they may have made. Additionally, it provides a clear example of how to calculate slope using the given points, helping students further develop their problem-solving skills.
Finding Slope from Two Points Coloring Activity Answer Key Pumpkin
The finding slope from two points coloring activity answer key for the pumpkin theme is a helpful resource for students to practice their understanding of slope in a fun and engaging way. By using the given answer key, students can confidently check their work and identify any mistakes they may have made during the activity.
The pumpkin theme adds an extra element of excitement to the activity, making it more enjoyable for students. The answer key provides clear and concise explanations of how to find the slope between two given points on a graph. With this information, students can easily understand and apply the concept of slope to different real-world situations, such as determining the rate of change in a pumpkin’s growth or the steepness of a hill.
Here is an example of how the answer key may look:
| Point 1 | Point 2 | Slope |
|---|---|---|
| (2, 4) | (6, 10) | m = 2 |
| (-3, 7) | (1, 9) | m = 0.5 |
| (-1, 2) | (3, -2) | m = -1 |
By using the answer key, students can easily verify if they have correctly calculated the slope between any given set of points. This feedback is crucial for their learning and helps them build confidence in their mathematical skills. The pumpkin theme adds a touch of fun to the activity, making it an enjoyable and educational experience for students.
What is Finding Slope from Two Points?

Finding Slope from Two Points is a mathematical concept used to determine the steepness or gradient of a line between two given points in a coordinate plane. It is an important skill in algebra and is commonly used in various fields such as physics, engineering, and economics.
When we talk about finding the slope from two points, we are essentially calculating the ratio of the vertical change (the difference in the y-coordinates) to the horizontal change (the difference in the x-coordinates) between the two points. This ratio is often represented by the letter “m” and is referred to as the slope of the line.
To find the slope from two points, we can use the formula: m = (y2 – y1) / (x2 – x1). By plugging in the coordinates of the two points into this formula, we can easily calculate the slope. The slope can be positive, negative, zero, or undefined, depending on the direction and steepness of the line.
Understanding how to find the slope from two points is essential for graphing linear equations, solving equations involving lines, and analyzing the properties of lines. It allows us to identify whether a line is increasing or decreasing, its steepness, and its relationship to other lines or equations.
Practicing and mastering the skill of finding slope from two points is crucial for students studying algebra and is a fundamental concept in calculus and higher-level mathematics. It provides a foundation for further exploration of linear equations, functions, and the study of lines and their properties.
Why is Finding Slope from Two Points Important?

Understanding how to find the slope from two given points is an essential skill in mathematics and other fields that involve analyzing data and patterns. The slope represents the rate of change between two points on a graph, and it provides valuable information about the relationship between variables or the direction and steepness of a line.
One important application of finding slope from two points is in physics, where it is used to determine the velocity or speed of an object. By measuring the change in position over time, it is possible to calculate the slope, which represents the object’s speed. This information is crucial in fields such as mechanics, kinematics, and fluid dynamics, where understanding how objects move and interact with each other is essential.
In addition to physics, finding slope from two points is also important in fields such as engineering, economics, and computer science. Engineers use slope to design structures that can withstand certain forces and pressures. Economists analyze the changes in variables such as supply and demand to determine market trends and make informed decisions. Computer scientists use slope to design algorithms and data analysis techniques to process and interpret large datasets.
Overall, finding slope from two points is a fundamental concept with wide-ranging applications in various fields. It allows us to analyze and interpret data, make predictions, and understand the relationships between variables. Whether it is calculating velocities, designing structures, or analyzing market trends, the ability to find slope from two points is an important skill for problem-solving and decision-making in many disciplines.
How to Find Slope from Two Points

When working with linear equations and graphs, finding the slope between two points is an essential skill. The slope represents the steepness of the line and can help determine the rate of change.
To find the slope between two points, you need to know their coordinates. Let’s say we have two points, (x₁, y₁) and (x₂, y₂). The slope (m) can be calculated using the formula:
m = (y₂ – y₁) / (x₂ – x₁)
This equation subtracts the y-coordinates of the two points and divides it by the difference in the x-coordinates. This calculation gives you the slope of the line that passes through these two points. Remember that the slope can be positive, negative, zero, or undefined.
Let’s illustrate this with an example. Consider two points, (2, 4) and (5, 10). To find the slope between these two points, we plug their coordinates into the slope formula:
m = (10 – 4) / (5 – 2)
Simplifying this, we get:
m = 6 / 3
Therefore, the slope between the points (2, 4) and (5, 10) is 2. This means that for every unit increase in the x-coordinate, the y-coordinate will increase by 2 units.
Finding the slope between two points is a fundamental concept in algebra and is crucial for understanding linear equations and graphs. Practice this skill using different points to reinforce your understanding and improve your overall math proficiency.
Pumpkin Coloring Activity: Finding Slope from Two Points
In this pumpkin coloring activity, students will practice finding the slope of a line given two points. This activity is a fun and engaging way to reinforce the concept of slope and improve students’ understanding of how to calculate it.
The activity consists of a worksheet with several pumpkins, each labeled with two points. Students are instructed to find the slope between the two points and color the corresponding pumpkin according to the given key. The key assigns different colors to different slopes, allowing students to create a colorful picture as they correctly calculate the slopes.
This activity not only helps students practice finding slope, but also reinforces their ability to plot points on a graph and visualize the slope of a line. It encourages critical thinking as students analyze the relationship between two points and determine the steepness or direction of the line connecting them.
By engaging in this hands-on activity, students can develop a deeper understanding of slope and enhance their overall math skills. It provides a visual representation of slope, making it easier for students to grasp the concept and apply it to real-world situations. Additionally, the interactive nature of the activity makes it more enjoyable and memorable for students, helping them actively participate in their own learning.
Example Worksheet:
| Pumpkin Number | Point 1 | Point 2 | Slope | Color |
|---|---|---|---|---|
| Pumpkin 1 | (2, 4) | (6, 8) | 1 | Red |
| Pumpkin 2 | (3, 7) | (9, 13) | 1 | Red |
| Pumpkin 3 | (-1, -3) | (-5, -7) | 1 | Red |
| Pumpkin 4 | (-2, 5) | (-4, 10) | 2.5 | Green |
| Pumpkin 5 | (0, 1) | (4, 9) | 2 | Green |
Answer Key: Pumpkin Coloring Activity
The answer key to the pumpkin coloring activity provides the correct slope values for each line segment between two points on the graph. This activity is designed to help students practice finding the slope of a line using the slope formula and two given points.
The answer key is organized in a table format, with each row representing a different line segment. The table includes the coordinates of the two points for each line segment, as well as the slope value. The slope values are calculated by plugging the coordinates into the slope formula, which is slope = (Y2 – Y1) / (X2 – X1). The answer key clearly shows the step-by-step calculations for each line segment, helping students understand the process of finding the slope.
The pumpkin coloring activity is a fun and engaging way for students to practice finding slope. By coloring in the pumpkin according to the correct slope values, students can see a visual representation of how the slope changes between different points on the graph. This activity also allows for creativity, as students can choose their own colors and patterns to fill in the pumpkin.
Overall, the answer key to the pumpkin coloring activity serves as a valuable resource for both students and teachers. It provides the correct slope values for each line segment, helping students check their work and assess their understanding of the concept. Additionally, the activity itself is an enjoyable way for students to practice and reinforce their knowledge of finding slope.
Tips and Tricks for Finding Slope from Two Points
When working with slope, it’s important to understand the formula for finding it from two points. The formula is:
Slope = (y2 – y1) / (x2 – x1)
This formula represents the change in the y-values divided by the change in the x-values between two points. Here are some tips and tricks to make finding slope easier:
- Identify the two points: Before you can calculate the slope, you need to identify the two points on the graph. These points are usually given in the form (x1, y1) and (x2, y2).
- Label the x and y coordinates: Once you have identified the points, label them as (x1, y1) and (x2, y2). This will help you keep track of which values to use in the formula.
- Substitute the values into the formula: Plug the values of the x and y coordinates into the slope formula. Subtract the y-values and the x-values to calculate the differences, and then divide the differences to find the slope.
- Simplify the result: After calculating the slope, simplify the result if possible. This means reducing fractions or expressing the slope as a decimal or fraction, depending on the context.
Following these tips and tricks will help you find the slope between two points more effectively. Practice using the slope formula with various examples to improve your skills in finding slope quickly and accurately.