
In the world of geometry, polygons are an essential concept to understand. A polygon is a closed shape with straight sides, and angles are a key component of these shapes. In order to fully grasp the characteristics and measurements of polygons, it is necessary to delve into the study of angles. This article will explore the topic of angles in polygons, specifically focusing on finding answers to Geometry 6 1.
Geometry 6 1 tackles the concept of angles in polygons, providing students with the opportunity to gain a deeper understanding of how to calculate and measure angles within these shapes. By studying this topic, students can improve their problem-solving skills and develop a solid foundation in geometry.
Understanding the answers to Geometry 6 1 involves exploring various properties and theorems related to angles in polygons. These properties include the sum of interior and exterior angles, as well as relationships between angles in regular and irregular polygons. By applying these properties and theorems, students can solve problems related to finding missing angles or determining the type of polygon based on given angle measurements.
What are polygons?

A polygon is a two-dimensional shape that is made up of straight lines called sides. It is a closed figure, which means that all of its sides are connected and it has no openings. A polygon can have three or more sides, and the number of sides determines its specific name. For example, a polygon with three sides is called a triangle, while a polygon with four sides is called a quadrilateral.
Polygons can be classified based on the measures of their angles. An equilateral polygon has all of its sides and angles equal. An isosceles polygon has two sides and two angles equal. A scalene polygon has all of its sides and angles different. Regular polygons are equilateral and equiangular, meaning they have both equal sides and equal angles.
Polygons are commonly used in everyday life. They can be found in various objects such as kitchen tiles, windows, and road signs. They are also used in architecture and design to create structures with specific shapes. Understanding the properties and characteristics of polygons is important in fields such as mathematics, engineering, and geometry. By studying polygons, we can better understand and analyze the world around us.
Understanding angles in polygons
Angles in polygons are a fundamental concept in geometry that play a crucial role in understanding the properties and characteristics of various shapes. A polygon is a closed figure with three or more straight sides. Each side of a polygon intersects at a vertex, creating angles at each vertex.
Identifying angles:
When examining angles in polygons, it’s important to be able to identify and understand various types of angles. Some common types of angles in polygons include:
- Interior angles: These angles are formed inside the polygon at each vertex.
- Exterior angles: These angles are formed by extending one side of the polygon and measuring the angle outside the polygon at the vertex.
- Central angles: These angles are formed by drawing a line from the center of the polygon to a vertex, creating an angle.
Sum of angles:
Another important concept in understanding angles in polygons is the sum of angles in a polygon. The sum of the interior angles of a polygon can be found using the formula: (n-2) x 180, where n represents the number of sides in the polygon. This formula can be used to find the sum of angles in any polygon, regardless of its size or shape.
Using angles to classify polygons:
By examining the angles in a polygon, we can classify polygons into different categories based on their angles. For example, a regular polygon has all angles congruent and all sides equal in length. An equiangular polygon has all angles congruent but may have sides of different lengths. These classifications help us understand and describe the properties of different polygons.
In conclusion, understanding angles in polygons is essential for comprehending the properties and characteristics of different shapes. By identifying angles, calculating their sum, and using angles to classify polygons, we can gain a deeper understanding of the geometry of polygons. This knowledge has practical applications in fields such as architecture, engineering, and design.
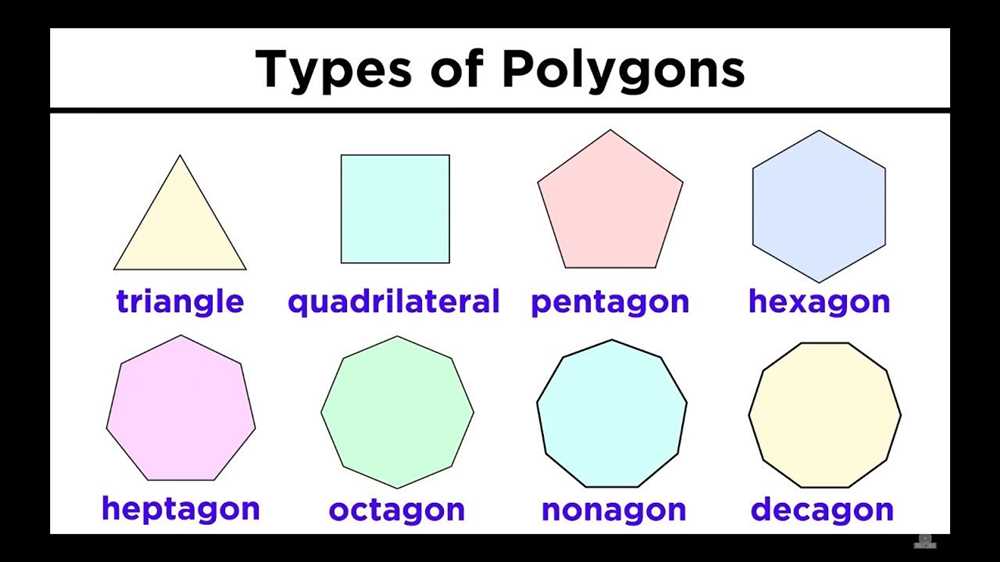
Types of polygons
A polygon is a two-dimensional figure that is made up of straight sides and angles. There are several types of polygons, each with its own unique characteristics.
1. Triangle: A triangle is a polygon with three sides and three angles. The sum of the interior angles of a triangle is always 180 degrees. Triangles can be further classified into different types based on the length of their sides, such as equilateral, isosceles, and scalene triangles.
2. Quadrilateral: A quadrilateral is a polygon with four sides and four angles. The sum of the interior angles of a quadrilateral is always 360 degrees. Quadrilaterals can be classified into different types based on their angles and side lengths, such as squares, rectangles, parallelograms, and trapezoids.
3. Pentagon: A pentagon is a polygon with five sides and five angles. The sum of the interior angles of a pentagon is always 540 degrees. Pentagon shapes can have equal or unequal side lengths.
4. Hexagon: A hexagon is a polygon with six sides and six angles. The sum of the interior angles of a hexagon is always 720 degrees. Hexagons can have equal or unequal side lengths.
5. Octagon: An octagon is a polygon with eight sides and eight angles. The sum of the interior angles of an octagon is always 1080 degrees. Octagons can have equal or unequal side lengths.
These are just a few examples of polygons, and there are many other types with different numbers of sides and angles. Understanding the properties and characteristics of each type of polygon is essential in geometry and helps in solving problems related to shapes and measurements.
Triangles
In geometry, a triangle is a polygon with three sides and three angles. It is one of the fundamental shapes in Euclidean geometry. Triangles can be classified based on their sides and angles. There are several types of triangles, including equilateral triangles, isosceles triangles, and scalene triangles.
An equilateral triangle has three equal sides and three equal angles, each measuring 60 degrees. This type of triangle is symmetrical and can be found in various contexts, such as the shape of a traffic sign or the structure of a pyramid.
An isosceles triangle has two equal sides and two equal angles. The non-equal angle is referred to as the base angle, while the two equal angles are called the congruent angles. The sum of the congruent angles is always greater than the base angle.
A scalene triangle has no equal sides and no equal angles. Each side and angle of a scalene triangle is unique. This type of triangle often appears in irregular shapes, such as the outline of landforms or the design of book covers.
Triangles have various properties and formulas that can be used to calculate their angles, sides, and areas. The Pythagorean theorem is an important concept in triangles, which states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is often used to solve problems involving right triangles.
In summary, triangles are essential geometric shapes with distinct properties and classifications. They are widely used in countless applications, ranging from architectural designs to mathematical calculations. Understanding the different types of triangles and their characteristics is crucial for various fields of study.
Quadrilaterals
A quadrilateral is a polygon with four sides. It is formed by connecting four points in a plane, with each point representing a vertex of the quadrilateral. The sides of a quadrilateral can be of different lengths and can be straight or curved. In addition, the angles formed by the sides of a quadrilateral can vary.
There are several types of quadrilaterals, each with its own unique properties. One common type is the rectangle, which has four right angles and opposite sides that are equal in length. Another type is the square, which is a special case of a rectangle with all four sides equal in length. The square also has four right angles. The parallelogram is another type of quadrilateral, with opposite sides that are parallel and equal in length. It does not have any right angles.
The trapezoid is a quadrilateral with one pair of parallel sides. The two non-parallel sides of a trapezoid are called the legs, while the parallel sides are called the bases. The rhombus is a quadrilateral with all four sides equal in length. It does not have any right angles. The kite is another type of quadrilateral, with two pairs of adjacent sides that are equal in length.
In summary, quadrilaterals are polygons with four sides. They come in various types, including rectangles, squares, parallelograms, trapezoids, rhombuses, and kites. Each type has its own unique attributes, such as the presence of right angles, parallel sides, or equal side lengths. Understanding the properties of quadrilaterals is important in geometry and can help in solving problems involving angles and polygon measurements.
Pentagons
A pentagon is a polygon with five sides. The word “pentagon” comes from the Greek words “penta,” meaning five, and “gonia,” meaning angle. A regular pentagon has five equal sides and five equal angles.
The sum of the interior angles of a pentagon is always 540 degrees. This can be calculated using the formula (n-2) * 180, where n is the number of sides of the polygon. In the case of a pentagon, (5-2) * 180 = 540.
In a regular pentagon, each interior angle measures 108 degrees. This can be calculated by dividing the sum of the interior angles (540 degrees) by the number of angles (5).
Some examples of real-life pentagons include the shape of a home plate in baseball, the design of the Pentagon building in Washington, D.C., and the shape of a star when drawn with five straight lines.
When working with pentagons, it is important to understand their properties and the relationships between their sides and angles. By studying pentagons, mathematicians and engineers can design structures and solve complex problems in various fields, such as architecture and engineering.
Hexagons

A hexagon is a polygon with six sides and six angles. It is a two-dimensional shape that can be classified as a regular hexagon or an irregular hexagon. In a regular hexagon, all six sides are equal in length, and all six angles are equal. In an irregular hexagon, the sides and angles can have different measurements.
One of the key properties of a hexagon is that the sum of all its interior angles is equal to 720 degrees. This can be derived using the formula 180(n-2), where n represents the number of sides. In the case of a hexagon, this formula gives us 180(6-2), which equals 720 degrees.
A hexagon can have various geometric applications. One common example is the honeycomb pattern found in beehives. Bees build hexagonal cells to store honey and raise their young because this shape allows for efficient use of space and provides strong structural support.
In addition, hexagons are frequently used in tiling patterns. Their regular shape and the way they fit together make them ideal for creating visually appealing and symmetrical designs. Hexagonal tiles can be found in various settings, such as bathrooms, kitchens, and outdoor spaces.
Overall, the hexagon is a versatile and interesting polygon that has practical applications in nature and design. Its unique properties and geometric characteristics make it a fascinating shape to study and explore.
Properties of angles in polygons

The study of angles in polygons is an important aspect of geometry. Understanding the properties of angles in polygons helps us analyze and solve geometric problems more effectively.
One key property of angles in polygons is that the sum of the interior angles in any polygon can be found using the formula (n-2) * 180 degrees, where n represents the number of sides in the polygon. This formula allows us to easily determine the total measure of the interior angles in a polygon without having to individually calculate each angle.
Another property of angles in polygons is that the exterior angle of a polygon is equal to the sum of the two non-adjacent interior angles. This property can be used to find the measure of an exterior angle in a polygon when the measures of the corresponding interior angles are known.
Additionally, regular polygons have some special properties when it comes to their angles. In a regular polygon, all interior angles are congruent, meaning they have the same measure. The measure of each interior angle in a regular polygon can be found using the formula 180 * (n-2) / n, where n represents the number of sides in the polygon. This formula allows us to easily calculate the measure of each interior angle in a regular polygon.
In conclusion, understanding the properties of angles in polygons is essential in analyzing and solving geometric problems. These properties, such as the sum of interior angles and the relationship between interior and exterior angles, allow us to make calculations and deductions about angles in polygons more efficiently. Additionally, regular polygons have their own special properties when it comes to angles, making them a particularly interesting and important topic in geometry.
Sum of Interior Angles
The sum of the interior angles of a polygon is determined by the number of sides it has. The formula to calculate the sum of the interior angles of a polygon is (n-2) * 180 degrees, where n is the number of sides of the polygon. This formula applies to all polygons, regardless of their shape or size.
For example, in a triangle (a polygon with three sides), the sum of the interior angles is (3-2) * 180 = 180 degrees. In a quadrilateral (a polygon with four sides), the sum of the interior angles is (4-2) * 180 = 360 degrees. As the number of sides increases, the sum of the interior angles also increases.
This formula can be used to find the measure of each interior angle in a regular polygon, where all sides and angles are equal. To find the measure of each interior angle, we divide the sum of the interior angles by the number of sides. For example, in a regular pentagon (a polygon with five sides), the sum of the interior angles is (5-2) * 180 = 540 degrees. Dividing 540 by 5 gives us each interior angle measure of 108 degrees.
In conclusion, the sum of interior angles in a polygon can be calculated using the formula (n-2) * 180 degrees, where n is the number of sides. This formula is applicable to all polygons and can be used to find the measure of each interior angle in a regular polygon.