
Geometry, the study of shapes and their properties, plays a crucial role in many fields, from engineering and architecture to art and design. In Chapter 6 of a typical geometry textbook, students are introduced to the concept of polygons and their various characteristics. This review answer key provides a comprehensive overview of the main topics covered in this chapter, serving as a useful tool for students looking to test their understanding and prepare for upcoming assessments.
One of the key topics in Chapter 6 is the classification of polygons based on their number of sides. Students will learn about various types of polygons, such as triangles, quadrilaterals, pentagons, and hexagons. Understanding the properties of each type of polygon is essential for recognizing and working with them in problem-solving situations.
In addition to classifying polygons, Chapter 6 explores different ways to measure and calculate their various properties. Students will learn about perimeter, the distance around a polygon, as well as area, the measure of the space enclosed by a polygon. Through exercises and examples, students will gain hands-on experience in calculating the perimeter and area of different polygons.
Furthermore, Chapter 6 introduces students to the concept of symmetry in polygons. Students will explore how some polygons can be divided into two equal halves that mirror each other. Understanding symmetry is not only aesthetically pleasing but also crucial in fields such as architecture and design, where symmetrical shapes are often used to create balance and harmony.
This geometry chapter 6 review answer key serves as a valuable resource for students seeking to reinforce their understanding of polygons and their properties. By practicing with the provided answers, students can evaluate their knowledge and identify areas that may need further review. With this tool in hand, students can feel confident and prepared as they progress in their study of geometry.
Geometry Chapter 6 Review Answer Key: Explained and Simplified
In geometry, Chapter 6 deals with properties of polygons, including triangles and quadrilaterals. It explores different types of polygons and their characteristics. The review answer key for Chapter 6 provides explanations and simplifications for various concepts and problem-solving strategies related to polygons.
This answer key is a valuable resource for students studying geometry as it helps them understand and apply the principles covered in Chapter 6. It breaks down complex ideas into simpler terms and provides step-by-step explanations for solving problems.
- Triangle properties: The review answer key explains key properties of triangles, including angle sums, side lengths, and relationships between angles. It provides examples and diagrams to illustrate these concepts and offers strategies for solving triangle-related problems.
- Quadrilateral properties: The answer key also covers various properties of quadrilaterals, such as parallel sides, opposite angles, and diagonals. It demonstrates how to determine the type of quadrilateral based on given information and provides formulas for finding perimeter and area.
- Problem-solving strategies: The answer key includes problem-solving strategies that can be used to simplify and solve complex polygon problems. These strategies involve breaking down the problem into smaller parts, using logical reasoning, and applying known properties of polygons.
In summary, the Geometry Chapter 6 Review Answer Key is a comprehensive resource for students studying polygons. It provides explanations, simplifications, and problem-solving strategies for various concepts related to triangles and quadrilaterals. By using this answer key, students can enhance their understanding of geometry and improve their problem-solving skills in this area.
Overview of Chapter 6: Geometric Proofs and Triangles

In Chapter 6 of the geometry textbook, we delve into the fascinating world of geometric proofs and explore the properties and relationships of triangles. This chapter is crucial for developing a solid understanding of geometry and its applications.
One of the main topics covered in this chapter is geometric proofs. We learn how to use deductive reasoning and logical arguments to prove theorems and statements about angles, triangles, and other geometric shapes. Through step-by-step reasoning, we can establish the validity of mathematical statements and build a strong foundation in geometric logic.
The chapter also focuses on the properties and classifications of triangles. We examine the different types of triangles, such as equilateral, isosceles, and scalene, and learn to identify their unique characteristics. By understanding the properties of triangles, we can solve various problems and analyze their relationships with other geometric figures.
Additionally, we explore triangle congruence and similarity. We learn about the criteria for proving triangles congruent, including side-angle-side (SAS), side-side-side (SSS), angle-side-angle (ASA), and angle-angle-side (AAS). Understanding triangle congruence allows us to determine if two triangles are identical and apply their properties in various geometric scenarios.
By the end of Chapter 6, students will have gained a comprehensive understanding of geometric proofs and triangles. These foundational concepts are essential for further exploration in geometry and provide a solid basis for solving more complex geometric problems in future chapters.
Importance of Understanding Chapter 6 Concepts
Chapter 6 in geometry introduces several key concepts that are important for building a strong foundation in the subject. Understanding these concepts is crucial for success not only in this chapter but also in future chapters and applications of geometry in real-life situations.
1. Parallel Lines and Transversals: One of the main topics covered in Chapter 6 is the concept of parallel lines and transversals. This knowledge is essential for understanding angles and their relationships, such as corresponding angles, alternate interior angles, and alternate exterior angles. These concepts have applications in various fields, including architecture, engineering, and design.
2. Angle Relationships: Another important concept in Chapter 6 is the understanding of different angle relationships. These include vertical angles, which are formed by two intersecting lines, and linear pairs, which are adjacent angles that add up to a straight angle. This knowledge is fundamental for solving problems involving angles and understanding geometric proofs.
3. Triangle Congruence: Chapter 6 also explores triangle congruence, which is essential for identifying and proving triangles that are congruent. Understanding triangle congruence helps in solving various geometric problems, such as determining the measures of unknown angles or sides in a triangle or proving that two triangles are congruent.
4. Isosceles and Equilateral Triangles: Additionally, Chapter 6 introduces the concepts of isosceles and equilateral triangles. These types of triangles have specific properties and symmetries that are important to recognize. Understanding these properties helps in solving problems related to sides, angles, and perimeters of these special triangles.
5. Circle Terminology: Lastly, Chapter 6 covers circle terminology, including the different parts of a circle such as the radius, diameter, chord, secant, and tangent. Knowledge of these terms is crucial for solving problems involving circles, calculating arc lengths, and understanding the relationship between angles and arcs in a circle.
Overall, understanding the concepts covered in Chapter 6 of geometry is vital for building a solid foundation in the subject. These concepts lay the groundwork for further exploration in geometry and their applications in real-life situations. By mastering these concepts, students can enhance their problem-solving skills and develop a deeper understanding of geometric principles.
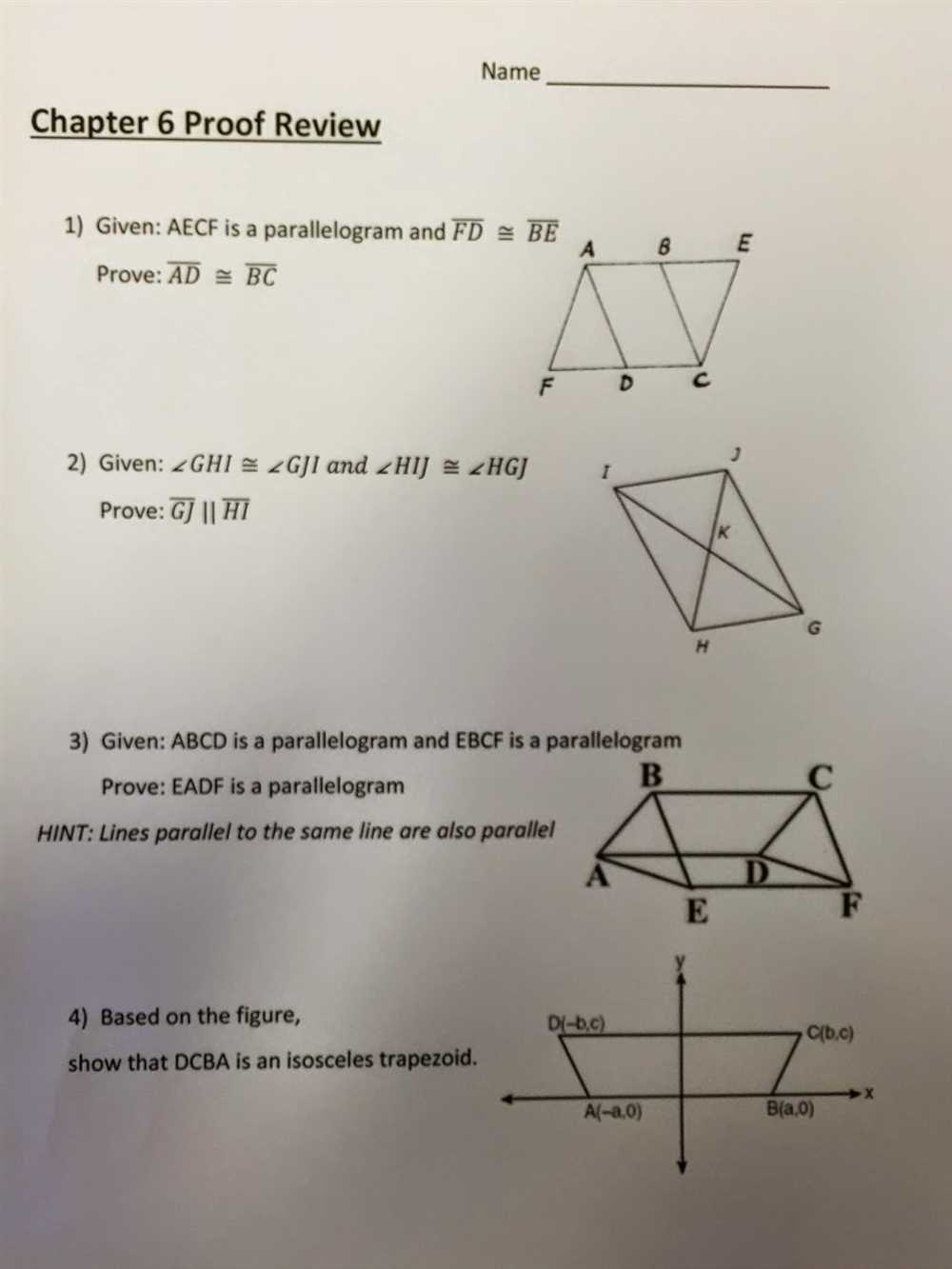
Key Concepts Covered in Chapter 6: Geometric Proofs and Triangles
In Chapter 6 of the Geometry textbook, students are introduced to the key concepts of geometric proofs and triangles. This chapter focuses on the different methods and strategies used to prove geometric theorems and properties, as well as the various properties and classifications of triangles.
Geometric Proofs: A geometric proof is a logical argument that uses deductive reasoning and mathematical principles to establish the truth of a geometric statement or theorem. The chapter covers the process of writing and structuring these proofs, including the use of statements and reasons, as well as the different types of proofs such as direct proofs, indirect proofs, and proof by contradiction.
Triangle Properties and Classification: Triangles are an essential part of geometry, and this chapter delves into the different properties and classifications of triangles. Students learn about the sum of angles in a triangle, the Triangle Inequality Theorem, and the relationships between the sides and angles of different types of triangles, including equilateral, isosceles, and scalene triangles. They also explore the various methods for proving triangle congruence, such as SSS, SAS, ASA, and AAS.
As students progress through Chapter 6, they will gain a deeper understanding of geometric proofs and triangles, learning how to apply these concepts to solve problems and prove geometric theorems. By mastering these key concepts, students will develop a strong foundation in geometry and be prepared to tackle more advanced topics in the subject.
Understanding the Answer Key: How to Use It Effectively
The answer key is a valuable resource for students studying geometry. It provides the correct answers to the questions or problems presented in the chapter review. However, simply looking at the answers and moving on may not be the most effective way to use the answer key. To truly benefit from this resource, students should approach it with a strategic mindset and follow a few key steps.
1. Attempt the problems on your own first: Before referring to the answer key, it is important to give the problems a genuine try. This allows students to engage with the material, apply their knowledge, and identify any areas where they may need additional practice. It also helps build problem-solving skills and boosts confidence.
2. Compare your answers with the answer key: Once you have attempted the problems, you can check your answers against the answer key. Pay close attention to the steps and methods used to arrive at the solutions. This will help you understand the reasoning behind the correct answers and identify any mistakes or misconceptions you may have had.
3. Analyze any incorrect answers or misconceptions: If you find that your answers do not match with those in the answer key, don’t immediately dismiss it as correct and move on. Instead, take the time to analyze your thought process and identify any errors or misconceptions that led to the incorrect answers. This self-reflection is crucial for learning and improving your understanding of the concepts.
4. Use the answer key as a learning tool: The answer key is not just a tool for checking answers; it is also a valuable learning tool. Use it to study the correct methods and approaches to problem solving. Pay attention to any patterns or strategies that can be applied to similar types of problems in the future. Take notes and create a study guide based on the solutions provided in the answer key.
5. Seek clarification or guidance if needed: If you are still unsure about a particular problem or concept, don’t hesitate to seek clarification or guidance from your teacher, classmates, or online resources. The answer key should not be the sole source of information; it should be used in conjunction with other resources to deepen your understanding of the subject.
By following these steps and using the answer key effectively, students can enhance their learning experience, improve their problem-solving skills, and gain a deeper understanding of geometric concepts.
Breakdown of Each Question and Solution in the Answer Key
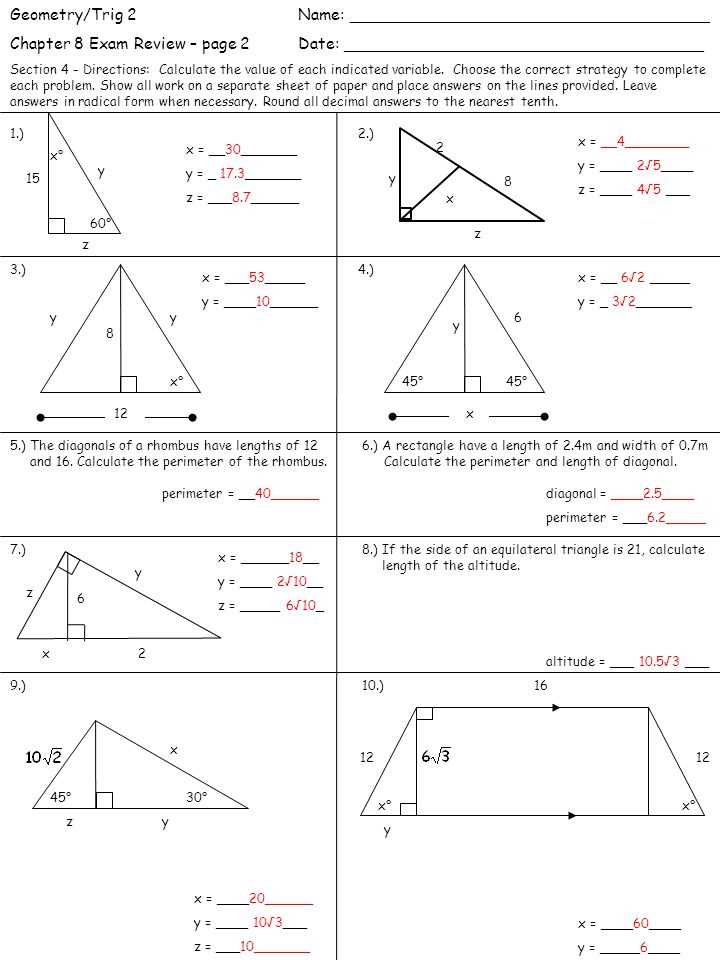
In the answer key for the Geometry chapter 6 review, there are several questions and solutions provided. Let’s break down each question and its corresponding solution to understand the concepts and techniques used.
Question 1: Find the area of a triangle with a base of 8 units and a height of 5 units.
This question involves calculating the area of a triangle using the formula A = 1/2 * base * height. In this case, the base is 8 units and the height is 5 units. Plugging these values into the formula, we get A = 1/2 * 8 * 5 = 20 square units. Therefore, the area of the triangle is 20 square units.
Question 2: Determine the volume of a rectangular prism with dimensions of 6 units, 4 units, and 3 units.
This question requires finding the volume of a rectangular prism, which can be done by multiplying the length, width, and height of the prism. In this case, the length is 6 units, the width is 4 units, and the height is 3 units. Multiplying these values together, we get 6 * 4 * 3 = 72 cubic units. Therefore, the volume of the rectangular prism is 72 cubic units.
Question 3: Solve for x in the equation 3x + 5 = 17.
This question involves solving a linear equation for the variable x. The equation 3x + 5 = 17 can be solved by subtracting 5 from both sides to isolate the term with x. This yields 3x = 12. Then, we divide both sides by 3 to solve for x, giving us x = 4. Therefore, the solution for x in the equation is 4.
Question 4: Find the circumference of a circle with a radius of 6 units.
To find the circumference of a circle, we can use the formula C = 2*pi*r, where r is the radius of the circle. In this case, the radius is 6 units. Plugging this value into the formula, we get C = 2*3.14*6 = 37.68 units. Therefore, the circumference of the circle is approximately 37.68 units.
Question 5: Determine the midpoint of the line segment with endpoints (2, 4) and (6, 8).
To find the midpoint of a line segment with given endpoints, we can use the midpoint formula, which states that the x-coordinate of the midpoint is the average of the x-coordinates of the endpoints, and the y-coordinate of the midpoint is the average of the y-coordinates of the endpoints. In this case, the x-coordinates of the endpoints are 2 and 6, and the y-coordinates are 4 and 8. Taking the average of these values, we get the midpoint coordinates (4, 6). Therefore, the midpoint of the line segment is (4, 6).
By breaking down each question and solution in the answer key, we can understand the underlying concepts and techniques used in geometry. This can help us improve our problem-solving skills and grasp the fundamentals of geometry more effectively.