
Geometry is a branch of mathematics that deals with the properties and relationships of shapes and spaces. It is a fundamental subject that helps us understand the world around us. To assess students’ understanding of the concepts learned in Unit 1, a Geometry Unit 1 Test is conducted.
The Geometry Unit 1 Test evaluates students’ knowledge of basic geometric principles, such as angles, lines, and shapes. It covers topics like the classifications of angles, the different types of lines, and the properties of polygons. This test serves as a comprehensive assessment of students’ understanding of the foundational concepts in geometry.
The Geometry Unit 1 Test consists of multiple-choice questions, short-answer questions, and problem-solving tasks. It requires students to identify and apply geometric principles to solve various problems and scenarios. This test not only measures their knowledge of the subject matter but also their ability to apply that knowledge in practical situations.
Geometry Unit 1 Test

In the study of geometry, a Unit 1 Test is an important evaluation tool that assesses students’ understanding of key concepts and skills introduced in the first unit of the course. This test typically covers topics such as points, lines, angles, and shapes, and requires students to demonstrate their knowledge through a variety of questions, including multiple choice, short answer, and problem-solving tasks.
One of the main objectives of a Unit 1 Test in geometry is to gauge students’ ability to identify and apply geometric principles and properties in real-world situations. This includes recognizing different types of angles (e.g., acute, obtuse, right), understanding the relationships between angles and lines (e.g., parallel, perpendicular), and using geometric formulas to calculate the perimeter, area, and volume of various shapes.
The Unit 1 Test is also designed to assess students’ critical thinking and problem-solving skills. They may be asked to analyze and interpret geometric diagrams, construct geometric figures, and provide logical justifications for their mathematical reasoning. By completing this assessment, students can demonstrate their proficiency in geometry and identify areas for further improvement and review.
- Key topics that may be covered in a Geometry Unit 1 Test include:
- Points, lines, and planes
- Angles and their properties
- Types of triangles
- Quadrilaterals and their properties
- Circles and their properties
- Perimeter, area, and volume calculations
- Coordinate geometry
- Transformational geometry
In conclusion, the Geometry Unit 1 Test serves as an important assessment tool for evaluating students’ understanding of key geometric concepts and their ability to apply them in various problem-solving tasks. By successfully completing this test, students can demonstrate their proficiency in geometry and lay a solid foundation for future topics in the course.
Basic Shapes
Geometry is the study of shapes and their properties. One of the fundamental concepts in geometry is understanding basic shapes. These shapes form the building blocks of more complex geometric figures and are essential to understanding various geometric concepts.
Triangles: Triangles are three-sided polygons. They are classified based on the length of their sides and the measurement of their angles. A right triangle has one angle measuring 90 degrees, while an equilateral triangle has all sides and angles equal.
Squares: A square is a four-sided polygon with all sides equal in length and all angles measuring 90 degrees. It is a special type of rectangle, where all four sides have the same length.
Rectangles: A rectangle is a four-sided polygon with opposite sides parallel and equal in length. The angles formed by the intersection of the sides are all right angles. Rectangles are widely used in everyday life, from the shape of windows and doors to the design of computer screens.
Circles: A circle is a two-dimensional shape that is perfectly round. It is defined as the locus of all points equidistant from a central point called the center. Circles are used in various applications, such as the design of wheels, plates, and coins.
Polygons: Polygons are closed figures formed by line segments. They can have any number of sides, provided that the sides do not intersect. Some examples of polygons include triangles, squares, pentagons, and hexagons.
Conclusion: Understanding basic shapes is essential to grasp more complex geometric concepts. By studying these shapes, we can build a solid foundation in geometry and apply it to various real-world scenarios.
Measurements and Units
In the study of geometry, measurements and units play a crucial role in determining the size, shape, and dimensions of various geometric figures. Measurements are the quantifiable attributes of an object or a shape, while units provide a standardized way of expressing those measurements.
When measuring geometric figures, it is important to use appropriate units that are consistent with the dimensions being measured. For example, if we are measuring the length of a line segment, we would typically use units such as centimeters or inches. On the other hand, when measuring the area of a two-dimensional shape, we would use square units such as square centimeters or square inches.
Key concepts:
- Measurements: Quantifiable attributes of an object or shape.
- Units: Standardized way of expressing measurements.
- Using appropriate units for specific dimensions.
In order to accurately measure and express the measurements of geometric figures, it is important to understand the concepts of precision and accuracy. Precision refers to the level of detail and exactness in the measurement, while accuracy refers to how closely the measurement aligns with the true or accepted value.
Key concepts:
- Precision: Level of detail and exactness in the measurement.
- Accuracy: How closely the measurement aligns with the true value.
In summary, measurements and units form the foundation of geometry, allowing us to quantify and compare the attributes of geometric figures. By using appropriate units and understanding concepts like precision and accuracy, we can ensure accurate and meaningful measurements in our study of geometry.
Lines and Angles
In geometry, lines and angles are fundamental concepts that help us understand the properties and relationships between different geometric figures. A line is a one-dimensional figure that extends infinitely in both directions and is represented by a straight line with arrows on both ends. It has no thickness and is composed of an infinite number of points. Lines can be intersecting, parallel, or perpendicular, and their properties can be analyzed using different geometrical tools and theorems.
Angles, on the other hand, are formed when two lines intersect. An angle is a measure of the opening between two lines, rays, or line segments. It is usually measured in degrees and is denoted by the symbol ∠. Angles can be classified based on their measurements and relationships with other angles. For example, an angle less than 90 degrees is called an acute angle, while an angle exactly equal to 90 degrees is called a right angle. Angles greater than 90 degrees and less than 180 degrees are called obtuse angles, and angles greater than 180 degrees are called reflex angles.
Understanding lines and angles is crucial in geometry as they form the basis for many geometric theorems and properties. For example, the sum of the angles in a triangle is always 180 degrees, and the opposite angles formed by two intersecting lines are always equal. The study of lines and angles also helps us solve problems related to shape congruence, similarity, and symmetry. By analyzing the relationships between lines and angles, we can determine the properties of different geometric figures and accurately measure their dimensions.
Furthermore, lines and angles play a significant role in real-life applications such as architecture, engineering, and design. Architects use geometric principles to create aesthetically pleasing and structurally sound buildings, while engineers rely on the properties of lines and angles to design bridges, roads, and other structures. Additionally, angles are instrumental in navigation and surveying, where precise measurements and calculations are necessary for accurate mapping and positioning.
In conclusion, lines and angles are fundamental concepts in geometry that help us understand the properties and relationships of different geometric figures. By studying lines and angles, we can analyze the properties of shapes, solve geometric problems, and apply these concepts in various real-life applications.
Triangles
In geometry, a triangle is a polygon with three edges and three vertices. It is one of the basic shapes studied in geometry. Triangles are categorized based on the length of their sides or the measure of their angles.
There are different types of triangles, including equilateral triangles, isosceles triangles, and scalene triangles. An equilateral triangle has three equal sides and three equal angles. An isosceles triangle has two equal sides and two equal angles. A scalene triangle has no equal sides or angles.
Triangles also have different properties, such as the sum of their interior angles is always 180 degrees. The longest side of a triangle is always opposite the largest angle. The area of a triangle can be calculated using the formula 1/2 * base * height.
Triangles are used in various applications in our everyday lives, such as in building structures, engineering, and navigation. They provide the foundation for understanding more complex geometric concepts and are an essential part of mathematical education.
Quadrilaterals
A quadrilateral is a polygon that has four sides, four angles, and four vertices. It is a two-dimensional shape that can be classified into different types based on its properties and characteristics. In this unit, we will explore the different types of quadrilaterals and their unique attributes.
One of the most common types of quadrilaterals is a rectangle. A rectangle is a quadrilateral with four right angles, meaning that each angle measures 90 degrees. It has two pairs of parallel sides, which are equal in length. The opposite sides of a rectangle are congruent, and the diagonals bisect each other. Rectangles are widely used in everyday life, from the walls of buildings to computer screens.
Another type of quadrilateral is a parallelogram. A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length and the opposite angles are congruent. The diagonals of a parallelogram bisect each other, but they do not necessarily intersect at a right angle. Examples of parallelograms include the shapes of signs on the road and the screens of smartphones.
- A square is a special type of rectangle and parallelogram that has all sides congruent and all angles measuring 90 degrees. It is a quadrilateral with four right angles and two pairs of parallel sides. Squares are often used in geometry as the basis for calculations and constructions.
- A rhombus is a special type of parallelogram that has all sides congruent. It is a quadrilateral with opposite angles that are congruent and diagonals that bisect each other at right angles. Rhombuses can be found in tile patterns and jewelry designs.
In conclusion, quadrilaterals are versatile shapes that have four sides, four angles, and four vertices. They can be classified into various types such as rectangles, parallelograms, squares, and rhombuses based on their unique properties. Understanding the characteristics and properties of quadrilaterals is essential in the study of geometry and in everyday applications.
Circles
Circles are one of the fundamental shapes in geometry. They are defined as a set of points in a plane that are all equidistant from a fixed center point. The distance from the center to any point on the circle is called the radius. The length of the circumference, which is the distance around the circle, can be calculated using the formula C = 2πr, where π is a mathematical constant approximately equal to 3.14159. Circles are often used in real-life applications, such as clock faces, wheels, and roundabouts.
One important property of circles is that all radii are equal in length. This means that any line segment connecting the center of a circle to a point on its circumference is the same length as any other line segment connecting the center to a different point on the circumference. Another important property is that the diameter of a circle is twice the length of its radius. The diameter is a line segment that passes through the center of the circle and has both endpoints on the circumference.
Properties of Circles:
- A circle is a set of points equidistant from a fixed center.
- The radius is the distance from the center to any point on the circle.
- The circumference is the distance around the circle and can be calculated using C = 2πr.
- All radii of a circle are equal in length.
- The diameter is twice the length of the radius and passes through the center.
In addition to these basic properties, circles have many interesting characteristics and relationships with other geometric shapes. They can intersect with other circles, creating points of tangency or common chords. They can also be inscribed in or circumscribed around other polygons, such as triangles or squares. Understanding the properties and relationships of circles is essential in solving geometric problems and analyzing real-world situations.
Review and Practice
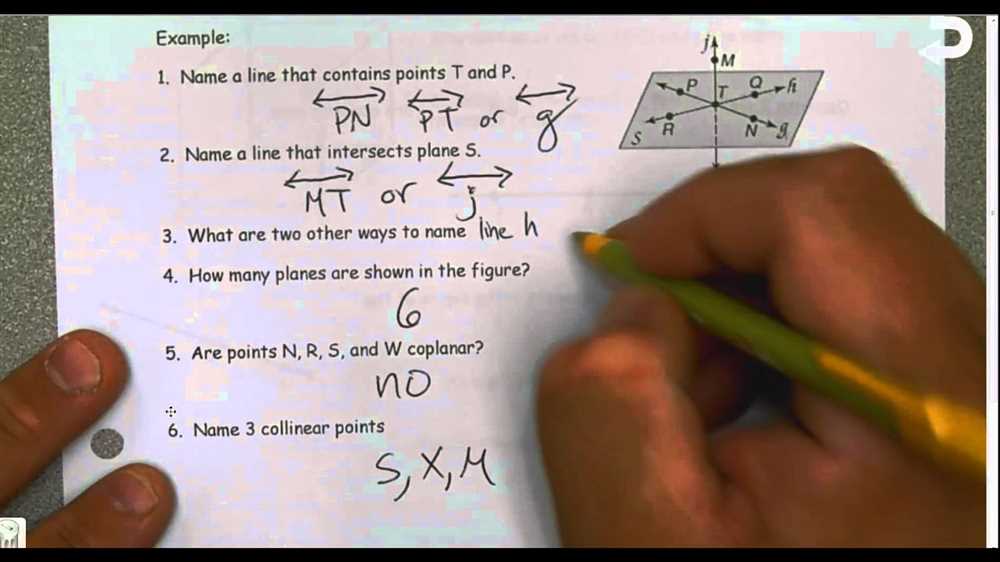
In preparation for the upcoming Geometry Unit 1 test, it is important to review and practice the key concepts and skills that have been covered in class. Understanding and applying these concepts will be crucial in successfully answering the test questions.
One of the main topics covered in Unit 1 is points, lines, and planes. Students should review the definitions and properties of these geometric figures. It is important to understand the relationship between points and lines, as well as the different types of lines (such as parallel, perpendicular, and intersecting lines). Additionally, students should be familiar with the concept of planes and how they are formed by points and lines.
Key concepts to review:
- Definition of a point, line, and plane
- Different types of lines
- Relationship between points and lines
- Definition of parallel, perpendicular, and intersecting lines
- Formation of planes by points and lines
Another important topic in Unit 1 is angles. Students should review the different types of angles (such as acute, obtuse, and right angles) and how to measure and classify them. It is crucial to understand the properties of angles, including vertical angles, adjacent angles, and complementary and supplementary angles.
Key concepts to review:
- Different types of angles
- Measurement and classification of angles
- Properties of angles, including vertical angles, adjacent angles, and complementary and supplementary angles
In addition to reviewing these key topics, it is important to practice solving problems and applying the concepts learned in class. Students should practice identifying geometric figures, measuring angles, and solving problems involving points, lines, and planes. This will help solidify their understanding of the material and prepare them for the Unit 1 test.