
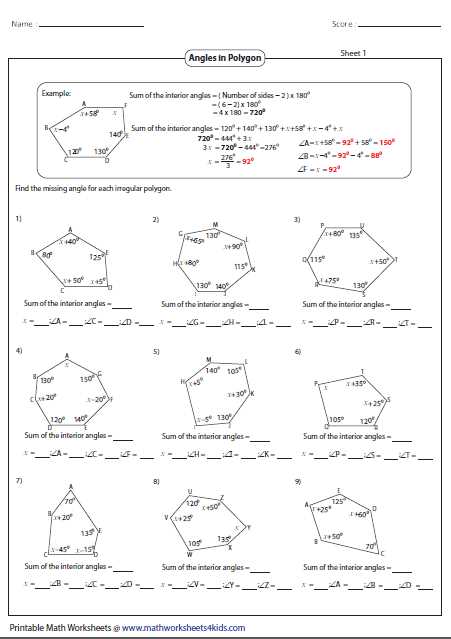
If you are studying geometry and looking for a way to practice and test your knowledge on the area of regular polygons, then this worksheet is perfect for you. In this article, we will provide you with an answer key to the geometry worksheet on the area of regular polygons. This will help you check your answers and ensure that you understand the concept fully.
The worksheet includes various questions that will challenge your understanding of the formula for finding the area of regular polygons. It covers different types of polygons, including triangles, squares, pentagons, hexagons, and octagons. Each question provides a diagram of the polygon and asks you to find the area using the given measurements.
By practicing with this worksheet and using the answer key provided, you will be able to reinforce your understanding of the concept and improve your problem-solving skills. It is important to grasp the formula and its application, as the area of regular polygons is a fundamental concept in geometry that is used in many real-life situations, such as calculating the area of rooms or fields.
Geometry Worksheet Area of Regular Polygons Answer Key
In geometry, the area of regular polygons is a key concept to understand. Regular polygons are polygons that have all sides and angles equal. Examples of regular polygons include equilateral triangles, squares, pentagons, hexagons, and so on. Finding the area of regular polygons requires knowledge of the length of one side and the number of sides.
To calculate the area of a regular polygon, you can use the formula: area = (1/4) * n * s^2 * cot(π/n), where n is the number of sides and s is the length of one side. This formula can be used for any regular polygon, regardless of the number of sides.
Example:
Let’s consider the example of finding the area of a regular hexagon. A hexagon has six sides, so n = 6. Let’s say the length of one side is 5 units, so s = 5. Substituting these values into the formula, we get:
area = (1/4) * 6 * 5^2 * cot(π/6)
Using a calculator, we can find that cot(π/6) is approximately equal to 1.732, so:
area = (1/4) * 6 * 5^2 * 1.732 = 6.892 units^2
Therefore, the area of the regular hexagon with a side length of 5 units is approximately 6.892 square units.
By using the formula and solving for the area, you can find the area of any regular polygon, given the number of sides and the length of one side. This concept is useful in various fields, including mathematics, engineering, and architecture.
Understanding Regular Polygons

A regular polygon is a shape with equal sides and equal angles. It is a fundamental concept in geometry, and understanding regular polygons is important for various mathematical applications.
Regular polygons are named based on the number of sides they have. For example, a polygon with 3 sides is called a triangle, a polygon with 4 sides is called a quadrilateral, and a polygon with 5 sides is called a pentagon. The list goes on with hexagon, heptagon, octagon, and so on.
Properties of Regular Polygons:
- A regular polygon has all sides of equal length.
- A regular polygon has all angles of equal measure.
- The sum of the interior angles of a regular polygon can be calculated using the formula (n-2) * 180 degrees, where n is the number of sides.
- The measure of each interior angle in a regular polygon can be found by dividing the sum of the interior angles by the number of sides.
Regular polygons are often used in various fields, such as architecture, engineering, and computer graphics. They have symmetrical properties that make them aesthetically pleasing in design. Understanding the area of regular polygons is also important, as it helps in calculating the space they occupy and determining their proportions in relation to other shapes.
Calculating the area of regular polygons:
- The formula to calculate the area of a regular polygon is A = (1/2) * ap, where A is the area, a is the apothem (the distance from the center of the polygon to the midpoint of any side), and p is the perimeter of the polygon.
- The apothem can be found using trigonometry or by dividing the length of one side by 2 times the tangent of half the measure of one interior angle.
Understanding the concept of regular polygons and their properties is essential for solving geometric problems and constructing complex shapes. It allows for precise measurements and accurate calculations in various practical scenarios.
What is the Area of a Regular Polygon?
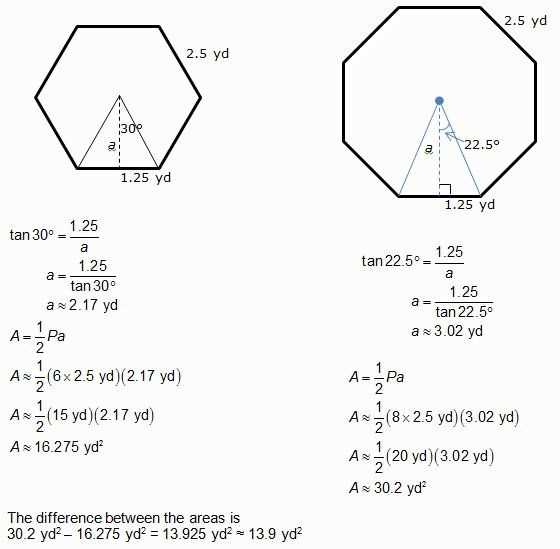
A regular polygon is a polygon that has equal sides and equal angles. This means that all the sides are the same length and all the interior angles are the same measure. Examples of regular polygons include squares, equilateral triangles, and regular hexagons. To find the area of a regular polygon, we need to know the length of one side and the number of sides.
The formula to calculate the area of a regular polygon is:
Area = (1/4) * n * s^2 * cot(π/n)
- n represents the number of sides of the polygon
- s represents the length of one side of the polygon
- π represents pi, approximately equal to 3.14159
- cot(π/n) represents the cotangent of π/n
To use this formula, simply substitute in the values for n and s into the equation and calculate the result. The cotangent function can be calculated using a calculator or mathematical software.
For example, if we have a regular pentagon with a side length of 5 units, we would substitute n = 5 and s = 5 into the formula. The calculation would look like this:
| Area = (1/4) * 5 * 5^2 * cot(π/5) |
|---|
| Area ≈ 6.88191 square units |
So, the area of the regular pentagon is approximately 6.88191 square units.
This formula allows us to find the area of any regular polygon, regardless of the number of sides. It is a useful tool for calculating the area of shapes in geometry and can be applied to various real-life situations.
Formula for Calculating the Area of a Regular Polygon
The area of a regular polygon can be calculated using a specific formula. A regular polygon is a polygon with all sides and angles equal. To find the area of a regular polygon, you need to know the length of one side and the number of sides.
The formula to calculate the area of a regular polygon is:
Area = (½) x (length of one side) x (apothem)
where the apothem is the distance from the center of the polygon to the midpoint of one of its sides. The length of one side can be easily measured, but the apothem may require additional calculations or measurements depending on the shape of the polygon.
To use the formula, simply substitute the values for the length of one side and the apothem. Multiply these values together, and then multiply the result by ½. The final answer will be the area of the regular polygon.
For example, let’s consider a regular hexagon with a side length of 5 units and an apothem of 4.5 units. Plugging these values into the formula:
- Area = (½) x 5 x 4.5
- Area = 11.25 square units
Therefore, the area of the regular hexagon is 11.25 square units.
By using the formula for calculating the area of a regular polygon, you can accurately determine the area of any regular polygon given its side length and apothem. This formula is a valuable tool for geometry and can be applied to various real-life scenarios involving regular polygons.
Practice Problems for Finding the Area of Regular Polygons
Calculating the area of regular polygons is an important skill in geometry, and practicing with various problems can help solidify your understanding of the concept. Regular polygons are polygons with equal sides and equal angles. The formula to find the area of a regular polygon is:
Area = (1/2) x apothem x perimeter
To find the area, you need to know the apothem (the distance from the center of the polygon to any of its sides) and the perimeter (the sum of all the sides of the polygon).
- Example 1: Find the area of a regular pentagon with side length 6 cm and apothem length 4 cm.
Solution: Since a regular pentagon has 5 sides, the perimeter is 5 times the side length, so the perimeter is 5 x 6 = 30 cm. Plugging the values into the formula, we get Area = (1/2) x 4 cm x 30 cm = 60 cm2. - Example 2: Determine the area of a regular hexagon with side length 8 in and apothem length 6 in.
Solution: A regular hexagon has 6 sides, so the perimeter is 6 x 8 = 48 inches. Applying the formula, we have Area = (1/2) x 6 in x 48 in = 144 in2. - Example 3: Calculate the area of a regular octagon with side length 12 m and apothem length 10 m.
Solution: The perimeter of a regular octagon is 8 times the side length, so the perimeter is 8 x 12 = 96 m. Plugging the values into the formula gives us Area = (1/2) x 10 m x 96 m = 480 m2.
Remember to use the formula for finding the area of regular polygons and practice with different examples to enhance your skills in this area of geometry. Understanding how to calculate the area of regular polygons will help you solve more complex geometric problems in the future.
Understanding the Answer Key Format
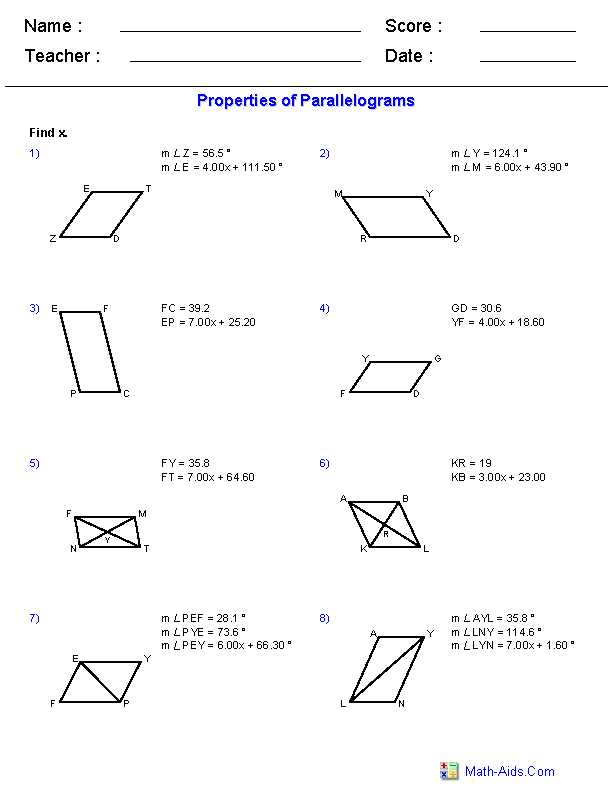
When it comes to completing a geometry worksheet on the area of regular polygons, having an answer key can be extremely helpful. However, understanding the format of the answer key is also important in order to successfully utilize it. The answer key typically contains the correct answers for each problem or question in the worksheet, allowing students to check their work and assess their understanding of the topic.
The answer key format usually consists of:
- Problem number: Each problem or question in the worksheet is assigned a number for easy reference.
- Correct answer: The answer key provides the correct answer to each problem, verifying whether the student’s solution is accurate.
For example:
| Problem Number | Correct Answer |
|---|---|
| 1 | 24 square units |
| 2 | 45 square units |
| 3 | 32 square units |
By referring to the answer key, students can compare their own answers with the correct ones to identify any mistakes they made or areas where they need further clarification. This process allows them to review the concepts and principles involved in finding the area of regular polygons and improve their problem-solving skills.
In addition, the answer key format serves as a valuable resource for teachers and educators. It helps them evaluate students’ performance, identify common misconceptions, and adjust their teaching strategies accordingly. By analyzing the patterns and trends in the mistakes made, educators can provide targeted interventions and support to enhance students’ understanding of geometry concepts.
Step-by-Step Solutions for Finding the Areas of Regular Polygons
When it comes to calculating the area of regular polygons, following a step-by-step approach can help simplify the process. By breaking down the problem into smaller, manageable parts, you can ensure accuracy and efficiency. Here is a guide to finding the area of regular polygons:
- Determine the type of regular polygon: Identify whether the polygon is a triangle, square, pentagon, hexagon, or any other regular polygon. Each polygon has a specific formula for calculating its area.
- Find the length of one side: Measure the length of one side of the regular polygon. This measurement will be needed in the area calculation.
- Find the apothem: The apothem is the distance from the center of the regular polygon to the midpoint of one of its sides. If the apothem is not given, it can be calculated using the formula apothem = side length / (2 * tan(180 / number of sides)).
- Calculate the area: Use the appropriate formula for the specific regular polygon. For example, the formula for the area of a triangle is 0.5 * base * height, while the formula for the area of a hexagon is 3 * (√3 * side length^2) / 2.
By following these steps, you can confidently find the area of regular polygons. Remember to use the correct formula for the specific polygon and always double-check your calculations for accuracy. Understanding these steps will help you tackle geometry problems involving regular polygons with ease.
Common Mistakes to Avoid
When solving a geometry worksheet on the area of regular polygons, it is important to be aware of common mistakes that students often make. By avoiding these mistakes, you can ensure that your answers are correct and that you fully understand the concept being taught.
1. Misinterpretation of the formula: One common mistake is misinterpreting or misapplying the formula for finding the area of a regular polygon. It is crucial to understand the formula and the variables involved before attempting to solve the problem.
2. Incorrect calculation of side lengths: Another mistake that can occur is miscalculating the length of the sides of the regular polygon. This can lead to incorrect calculations of the area. It is necessary to carefully measure or calculate the side lengths before proceeding with the formula.
3. Inaccurate use of units: Remember to always include the appropriate units when expressing your answer. Forgetting to include units or using incorrect units can result in a loss of points on the worksheet.
4. Not rounding correctly: Rounding errors can occur when working with decimal numbers. Be sure to follow the rounding rules specified in the worksheet instructions to avoid errors. In some cases, rounding too early or too late can lead to incorrect answers.
5. Oversight when counting angles: Regular polygons have equal interior angles. It is important to count the number of angles correctly to ensure that the correct formula is used and that the calculations are accurate.
To avoid these common mistakes, it is essential to carefully read and understand the instructions provided in the worksheet. Double-check your calculations and make sure you have a clear understanding of the concept of finding the area of regular polygons before attempting the problems.