
When studying systems of inequalities, it is important to understand how to graph and solve them. This process often involves finding the solutions to the system of equations by identifying the overlapping regions on a graph.
The “Graph Attack” method provides a step-by-step approach to solving these inequalities and finding their solutions. By utilizing graphing techniques, students can visually see the feasible regions and identify the solutions. This approach not only helps in developing graphing skills but also enhances understanding of linear programming and optimization.
Key components of the “Graph Attack” method include identifying the slope and intercepts of the inequalities, drawing the lines on a coordinate plane, shading the regions based on the inequality symbols, and finally identifying the common feasible region as the solution. This method enables students to efficiently solve systems of inequalities and find the exact solution set using graphs.
Solving systems of inequalities graphically
When solving systems of inequalities graphically, we are looking for the regions of the coordinate plane that satisfy all of the given inequalities. This is done by graphing each individual inequality and finding the overlapping regions.
To solve a system of inequalities graphically, we start by graphing each inequality on the same coordinate plane. This can be done by first identifying the boundary line for each inequality, which is usually a straight line. The inequality sign determines whether the boundary line should be solid or dashed. Next, we determine which side of each boundary line represents the solution set. This is usually done by picking a test point that is not on the boundary line and checking whether it satisfies the inequality or not.
After graphing all of the inequalities, we look for the overlapping regions. These are the areas that satisfy all of the given inequalities. The solution to the system of inequalities is the intersection of these regions.
We can also use shading to represent the solution set. The regions that satisfy all the inequalities are shaded, while the regions that do not satisfy at least one inequality remain unshaded. This makes it easier to visually identify the solution set.
Solving systems of inequalities graphically is a useful tool for understanding the solutions to a set of inequalities. It allows us to visualize the different regions that satisfy the inequalities and find their intersection. This method can be especially helpful when working with multiple inequalities and trying to find the overlapping solution sets.
Understanding key concepts in graphing systems of inequalities
Graphing systems of inequalities is an important skill in mathematics that allows us to visually represent and analyze multiple inequalities simultaneously. By graphing the solutions to each inequality on the same coordinate plane, we can determine the overlapping or non-overlapping regions that satisfy all the given inequalities.
When graphing systems of inequalities, it is essential to understand key concepts such as inequality symbols, shading, boundary lines, and intersection points.
The inequality symbols, such as <, >, <=, and >=, represent the relationship between two expressions. These symbols indicate whether the values on one side of the inequality are less than, greater than, less than or equal to, or greater than or equal to the values on the other side.
When graphing a system of inequalities, we use shading to indicate the region that satisfies the inequality. We shade the region above or below the boundary line, depending on the inequality symbol. For example, if the inequality is y < 2x + 3, we would shade the region below the boundary line because y is less than (<) the expression 2x + 3.
The boundary lines are the lines that separate the shaded regions and represent the solution to each individual inequality. These lines are usually solid or dashed, depending on whether the inequality is strict or non-strict. A solid line is used for inequalities such as <= or >=, while a dashed line is used for strict inequalities such as < or >.
In the graphing process, we can also identify intersection points, which are the points where the boundary lines of two or more inequalities intersect. These points represent the solutions that satisfy all the given inequalities simultaneously.
By understanding these key concepts and applying them effectively, we can accurately graph systems of inequalities and determine the regions that satisfy all the given inequalities, allowing us to solve real-world problems and make informed mathematical decisions.
Steps for Graphing Systems of Inequalities
In order to graph systems of inequalities, there are several steps that need to be followed. These steps ensure that the correct solution region is determined and accurately represented on the graph.
Step 1: Graph each inequality separately
Begin by graphing each inequality on its own set of axes. This allows you to visualize the individual solution regions for each inequality. Use different colors or shading to distinguish between the regions.
Step 2: Determine the overlapping region
Identify the overlapping region or the region that satisfies all of the inequalities in the system. This region represents the solution to the system of inequalities. It is important to carefully analyze the graphs and determine the overlapping area accurately.
Step 3: Represent the solution region
On a new set of axes, graph the solution region by combining the individual solution regions for each inequality. Use the same shading or color to represent the overlapping region determined in step 2. Make sure to label the axes and any important points or lines on the graph.
Step 4: Check the solution
Finally, check the solution by substituting test points into the original inequalities. If the test points satisfy all of the inequalities, then the solution region on the graph is correct. If not, review your work and make any necessary adjustments.
Following these steps will ensure that systems of inequalities are accurately graphed and that the solution region is correctly represented. It is important to pay attention to detail and carefully analyze the graphs to determine the correct overlapping region.
Using shading techniques to represent solutions
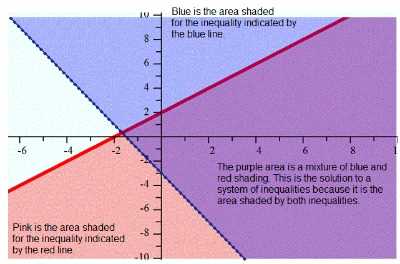
When graphing systems of inequalities, shading techniques are often used to represent the solutions graphically. Shading is used to visually distinguish the regions in the coordinate plane that satisfy the given system of inequalities. This allows for easier interpretation and analysis of the solution set.
A common way to represent solutions using shading is to shade the area that satisfies all the given inequalities. For example, if the inequalities form a system where the solution set is the region above a line and below another line, you would shade the region between the two lines. This shading indicates that any point within that shaded region represents a solution that satisfies both inequalities simultaneously.
Another shading technique that can be used is to shade the area outside the solution set. In this approach, the shaded region represents the values that do not satisfy the given system of inequalities. This can be particularly useful when dealing with complex systems of inequalities with multiple constraints, as it narrows down the possible solutions and helps to identify the points that do not meet the criteria.
Shading can also be combined with other graphical representations, such as dashed lines and arrows, to provide further clarity and information about the solution set. For instance, dashed lines can be used to represent “less than” or “greater than” inequalities, while arrows can indicate the direction in which the solutions extend.
In summary, shading techniques are an effective way to visually represent the solutions of systems of inequalities on a graph. They help to highlight the areas that satisfy or do not satisfy the given constraints, making it easier to understand and work with the solution set. By combining shading with other graphical representations, a comprehensive and informative visual representation can be created.
Analyzing and interpreting systems of inequalities
In mathematics, a system of inequalities consists of two or more inequalities with the same variables. By graphing these inequalities on a coordinate plane, we can analyze and interpret the solution set. This allows us to understand the range of values that satisfy all the inequalities simultaneously.
Graphing the system of inequalities helps visualize the relationship between the variables and identify regions that satisfy all the given conditions. The solution set can be determined by finding the overlapping or shaded area on the graph where all inequalities are true.
When interpreting the graph, it is important to pay attention to the line types and shading. Solid lines represent inequalities with “less than” or “greater than” signs, while dashed lines represent inequalities with “less than or equal to” or “greater than or equal to” signs. The shaded area represents the solution set, with a darkened region indicating strict inequality and a lightly shaded region indicating inclusive inequality.
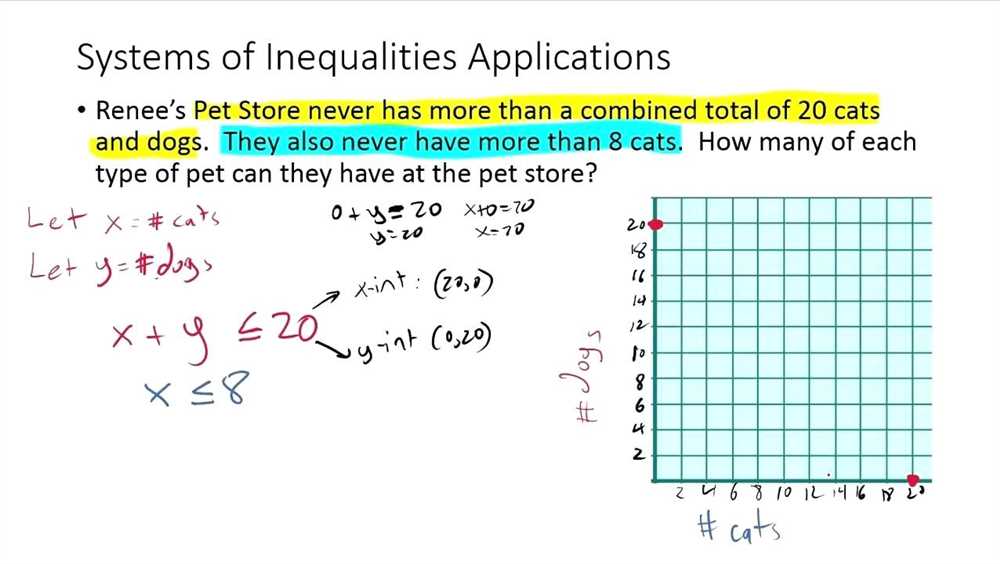
By analyzing and interpreting systems of inequalities, we can solve real-world problems involving multiple constraints. For example, we can use systems of inequalities to determine the feasible range of values for quantities such as production levels, budget allocations, or resource usage. This allows us to make informed decisions and optimize our outcomes based on the given constraints.
Practical applications of graphing systems of inequalities
Graphing systems of inequalities is a useful tool in various practical applications. It allows us to visually represent and analyze relationships between multiple variables and constraints. Here are a few practical scenarios where graphing systems of inequalities can be applied:
- Resource allocation: Graphing systems of inequalities can be used in optimizing resource allocation in industries such as manufacturing, agriculture, or transportation. By representing constraints, such as limited availability of resources or production capacities, the graph can help identify the optimal allocation that maximizes efficiency.
- Financial planning: Graphing systems of inequalities can assist in financial planning and budgeting. For example, it can help individuals or businesses determine the feasible range of expenses based on income, savings, and debt constraints. By representing these constraints on a graph, it becomes easier to make informed decisions and set realistic financial goals.
- Supply chain management: In supply chain management, graphing systems of inequalities can be used to optimize inventory levels and distribution strategies. By considering factors such as demand, transportation capacities, and storage limitations, the graph can help identify the most efficient routes and warehouse locations to minimize costs and maximize customer satisfaction.
- Environmental impact assessment: Graphing systems of inequalities can be applied in assessing and managing environmental impacts of human activities. By representing constraints such as pollution thresholds or habitat preservation areas, the graph can help identify sustainable development strategies that minimize negative environmental effects.
Overall, graphing systems of inequalities provide a valuable tool for analyzing and solving complex problems in various fields. They enable decision-makers to visualize constraints and relationships, allowing for more informed and optimal decision-making and resource allocation.


