In geometry, midsegments play a significant role in understanding the properties of triangles. In this article, we will provide the answer key for Homework 1 on triangle midsegments.
The concept of midsegments involves connecting the midpoints of two sides of a triangle to create a segment. These midsegments have some interesting properties that can help us solve various problems related to triangles. Homework 1 focuses on exploring these properties and applying them to solve different types of questions.
By using the answer key provided in this article, you will be able to check your solutions and understand the correct approach for each question. The answer key will guide you through the process of finding midpoints, determining lengths, and identifying relationships between midsegments and other elements of the triangle.
Homework 1 triangle midsegments answer key will not only help you improve your understanding of midsegments but also enhance your problem-solving skills in geometry. It is essential to practice these concepts repeatedly to reinforce your knowledge and apply them to more complex problems in the future.
Homework 1 Triangle Midsegments Answer Key

In triangle geometry, midsegments play an important role in understanding the properties and relationships between triangle sides and angles.
A midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. It is also known as a midline. Homework 1 focuses on finding the lengths of midsegments and using them to solve various problems.
To find the length of a midsegment, we can use the formula:
Length of Midsegment = 0.5 * (Length of the Side it connects)
The answer key for Homework 1 provides solutions to questions where students are asked to find the lengths of midsegments in different triangles. It also includes explanations and steps on how to arrive at the correct answers.
In addition to finding the lengths of midsegments, Homework 1 also explores the relationship between the midsegment and the parallel sides of a triangle. Students are asked to determine if midsegments are parallel to certain triangle sides and explain their reasoning.
The answer key for Homework 1 Triangle Midsegments provides a comprehensive guide for students to check their answers, learn from their mistakes, and deepen their understanding of the concept of midsegments in triangle geometry.
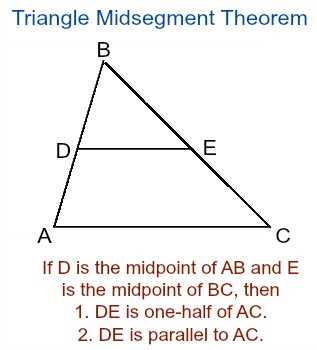
Understanding Midsegments of a Triangle

The midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. It is also known as a midline. Understanding the midsegments of a triangle is important in geometry as it helps us explore the relationships between different parts of a triangle.
Definition: The midsegment of a triangle is parallel to the third side of the triangle and half its length.
When we connect the midpoints of two sides of a triangle, we create a line segment that is parallel to the third side and half its length. This means that if we know the lengths of two sides of a triangle, we can easily determine the length of the midsegment.
For example: If we have a triangle with sides of lengths 8 cm, 10 cm, and 12 cm, we can find the length of the midsegment by adding the lengths of the two shorter sides and dividing by 2. In this case, the midsegment would have a length of (8 + 10) / 2 = 9 cm.
The midsegment of a triangle has several properties that make it useful in solving geometry problems. One important property is that the midsegment is always parallel to the third side of the triangle. This allows us to use the properties of parallel lines to find angles and lengths within the triangle.
Additionally, the midsegment divides the triangle into two smaller triangles with equal areas. This property allows us to use the midsegment to find the area of a triangle by finding the area of one of the smaller triangles and multiplying by 2.
In conclusion, understanding the midsegments of a triangle allows us to explore the relationships between different parts of a triangle and apply geometric properties to solve problems. The midsegment is a valuable tool in geometry and can help us find lengths, angles, and areas within a triangle.
Properties of Midsegments
A midsegment is a line segment that connects the midpoints of two sides of a triangle. It is also known as a midline or a median. Midsegments have several important properties that can be used to analyze and solve problems involving triangles.
1. Length: The length of a midsegment is equal to half the length of the third side of the triangle. This can be proven using the midpoint formula, which states that the coordinates of the midpoint of a line segment are the average of the coordinates of the endpoints. Therefore, if the midpoints of two sides of a triangle are connected by a midsegment, the length of the midsegment is equal to half the difference between the lengths of the two sides.
2. Parallelism: The midsegment of a triangle is parallel to the third side of the triangle. This can be proven using the concept of slope. If the slopes of two lines are equal, the lines are parallel. Since the midsegment connects the midpoints of two sides, its slope can be found by taking the difference in y-coordinates and dividing by the difference in x-coordinates of the two endpoints. If this slope is equal to the slope of the third side, then the midsegment is parallel to the third side.
These properties of midsegments are useful for solving problems involving triangle midsegments. By knowing the lengths and parallelism of midsegments, mathematicians can make accurate calculations and predictions about the properties of triangles and the relationships between their sides and angles.
Finding Midsegment Lengths
In geometry, a midsegment is a line segment that connects the midpoint of two sides of a triangle. It is also known as a median. Finding the length of midsegments can be useful in various geometric calculations and proofs.
To find the length of a midsegment, you need to know the lengths of the two sides it connects. The midsegment is always parallel to the third side of the triangle, and its length is equal to half the sum of the lengths of the two sides it connects.
One way to calculate the length of a midsegment is by using the midpoint formula. If you have the coordinates of the endpoints of the sides, you can find the midpoint of each side and then calculate the distance between the two midpoints. This will give you the length of the midsegment.
Another method to find the length of a midsegment is by using the properties of similar triangles. If the midsegment divides the third side of the triangle into two equal parts, then the triangles formed by the midsegment and each side of the triangle are similar. You can use the ratios of corresponding sides to find the length of the midsegment.
Finding midsegment lengths is an important concept in geometry, as it allows you to explore the relationships between various parts of a triangle. It can help you prove theorems, solve problems, and gain a deeper understanding of geometric principles.
Solving for Missing Midsegment Lengths
When working with triangles and midsegments, it is often necessary to find the lengths of missing midsegments in order to fully understand and analyze the properties of the triangle. This can be done using various methods and formulas depending on the given information.
One common approach to solving for missing midsegment lengths is using the properties of similar triangles. If two triangles are similar, their corresponding midsegments are also proportional in length. By setting up a proportion with the known midsegment lengths and the missing length, you can solve for the unknown length.
Another method to find missing midsegment lengths is by using the formula for the midpoint of a line segment. This formula states that the coordinates of the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) can be found by averaging the x-coordinates and the y-coordinates separately. By applying this formula to the given points of the triangle’s midsegments, you can find their lengths.
It is also important to remember the properties of midsegments. For example, the midsegment of a triangle is always parallel to the third side of the triangle and half its length. Using this property, you can find missing midsegment lengths by setting up equations based on the given lengths and the relationship between the midsegments and the sides of the triangle.
In conclusion, solving for missing midsegment lengths involves using different methods and formulas such as proportions, the midpoint formula, and the properties of midsegments. By applying these techniques and working with the given information, it is possible to determine the lengths of the missing midsegments and further analyze the properties of the triangle.
Using Midsegments to Find Triangle Areas

Midsegments are an important concept in geometry that can be used to find the areas of triangles. A midsegment is a line segment that connects the midpoints of two sides of a triangle. In any triangle, the three midsegments form a smaller triangle within the original triangle, known as the medial triangle. By understanding the properties of midsegments and the relationships between the medial triangle and the original triangle, we can calculate the area of the original triangle.
To find the area of a triangle using midsegments, we need to know the lengths of at least two midsegments. One way to find the midsegments is to use the midpoints of the sides of the triangle. The midpoints can be found by dividing the lengths of the sides in half. Once we have the midpoints, we can calculate the lengths of the midsegments using the distance formula.
Example:
- Let’s consider a triangle with sides of length 8, 10, and 12 units.
- Using the midpoints, we find that the midsegment connecting the midpoints of the sides of length 8 and 10 has a length of 9 units.
- The midsegment connecting the midpoints of the sides of length 8 and 12 has a length of 10 units.
- Now, we can use these midsegment lengths to calculate the area of the triangle.
- The area of the triangle is equal to half the product of the lengths of the midsegments.
- In this case, the area of the triangle is (9 * 10) / 2 = 45 square units.
By using midsegments, we can find the area of a triangle even if we don’t know the lengths of all the sides. This method can be helpful when dealing with complex or irregular triangles. It is a useful tool in geometry and can provide a deeper understanding of the relationships between different parts of a triangle.
Applying Midsegment Theorems in Real-life Scenarios
The concept of midsegments in geometry might seem abstract and disconnected from real-life scenarios, but they actually have practical applications in various fields. Understanding and applying midsegment theorems can provide insights and solutions in areas such as construction, engineering, and even sports.
In construction, midsegment theorems can be used to determine the optimal placement and alignment of supports or braces in structures. By identifying the midpoints of different segments, engineers can ensure the stability and balance of the construction. This is especially important in bridge design, where the midsegments of the different sections can help determine the distribution of weight and stress.
For example: When designing a suspension bridge, engineers need to calculate the midsegment of the main span to determine the ideal location for the main support towers. By ensuring that the midsegment passes through the midpoint of the span, the bridge can withstand the forces and ensure its safety.
In sports, midsegment theorems can also be applied to determine optimal strategies and positions. In team sports like soccer or basketball, understanding the midsegments of the playing field can help players position themselves strategically. By identifying the midpoints of certain areas or markings, players can maximize their coverage and create better passing and shooting angles.
For example: In soccer, knowing the midsegment of the field can help players position themselves between defenders and better utilize the available space. By aligning themselves with the midsegment, players can create passing lanes and opportunities for their teammates to advance towards the goal.
Overall, midsegment theorems may seem like abstract mathematical concepts, but they have practical applications in real-life scenarios. Whether it’s in construction, engineering, or sports, understanding and applying these theorems can lead to more efficient and effective solutions.
Practice Problems with Triangle Midsegments
In geometry, a midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. It is important to understand the properties and relationships of midsegments in order to solve problems involving triangles. Here are some practice problems to help reinforce your understanding of triangle midsegments.
Problem 1:
Given triangle ABC with midpoints D, E, and F of sides AB, BC, and AC respectively. If DE = 5 cm, EF = 7 cm, and DF = 8 cm, find the perimeter of triangle ABC.
Solution:
- Since DE, EF, and DF are midsegments of triangle ABC, they are each equal to half the length of their respective sides.
- This means that AB = 2 * DE = 2 * 5 cm = 10 cm, BC = 2 * EF = 2 * 7 cm = 14 cm, and AC = 2 * DF = 2 * 8 cm = 16 cm.
- The perimeter of triangle ABC is the sum of its side lengths, which is AB + BC + AC = 10 cm + 14 cm + 16 cm = 40 cm.
Problem 2:
Triangle XYZ has midpoints M, N, and P of sides XY, YZ, and XZ respectively. If XY = 12 cm and NP = 5 cm, find the length of side XZ.
Solution:
- Since NP is a midsegment of triangle XYZ, it is equal to half the length of side XZ.
- This means that XZ = 2 * NP = 2 * 5 cm = 10 cm.
- Therefore, the length of side XZ is 10 cm.
By practicing problems like these, you can strengthen your understanding of triangle midsegments and their properties. Remember to always use the properties and relationships of midsegments when solving problems involving triangles.