
Ice table problems are a common type of calculation in chemistry that involve determining the equilibrium concentrations of substances in a reaction. They are often used to solve for unknown equilibrium concentrations or to determine the value of various equilibrium constants. These problems can be complex, but with practice, they become easier to solve.
One way to approach ice table problems is to set up a table that tracks the changes in concentration of each species during the reaction. The table typically includes columns for initial concentration, change in concentration, and equilibrium concentration. By using the balanced chemical equation and the initial concentrations of the reactants and products, you can fill in the table and calculate the equilibrium concentrations.
For example, let’s consider a reaction where nitrogen dioxide (NO2) decomposes to form nitric oxide (NO) and oxygen (O2). The balanced chemical equation is: 2NO2(g) → 2NO(g) + O2(g). If the initial concentration of NO2 is 0.10 M, and the equilibrium concentration of NO is 0.050 M, we can use the ice table to find the equilibrium concentration of O2. By setting up the table and using the stoichiometry of the reaction, we can determine that the equilibrium concentration of O2 is 0.050 M as well.
In another example, let’s consider a reaction where hydrogen gas (H2) reacts with iodine gas (I2) to form hydrogen iodide (HI). The balanced chemical equation is: H2(g) + I2(g) → 2HI(g). If the initial concentration of H2 is 0.20 M and the initial concentration of I2 is 0.10 M, we can use the ice table to find the equilibrium concentration of HI. By setting up the table and using the stoichiometry of the reaction, we can determine that the equilibrium concentration of HI is 0.30 M.
Overall, ice table chemistry practice problems provide a valuable opportunity to apply your understanding of equilibrium concentrations and equilibrium constants in chemical reactions. By mastering the techniques for setting up and solving ice tables, you can enhance your problem-solving skills in the field of chemistry.
Ice Table Chemistry Practice Problems with Answers

Ice table problems are a common type of question in chemistry that involve calculating the equilibrium concentration of species in a chemical reaction. These problems require the use of an ice table, a systematic method for organizing and solving equilibrium problems.
To solve an ice table problem, you first need to write the balanced chemical equation for the reaction. Next, you fill out the ice table with the initial concentrations (if given), the change in concentration, and the equilibrium concentrations of the species involved in the reaction. The change in concentration is determined by the stoichiometry of the reaction.
For example, let’s consider the reaction:
N2(g) + 3H2(g) ⇌ 2NH3(g)
If the initial concentrations of N2 and H2 are both 0.20 M, and the equilibrium concentration of NH3 is 0.40 M, we can use the ice table to determine the change in concentration of each species:
| Species | Initial Concentration (M) | Change in Concentration (M) | Equilibrium Concentration (M) |
|---|---|---|---|
| N2 | 0.20 | -x | 0.20 – x |
| H2 | 0.20 | -3x | 0.20 – 3x |
| NH3 | 0 | +2x | 0.40 + 2x |
Since the stoichiometry of the reaction tells us that for every mole of N2 that reacts, three moles of H2 react, we can write an expression for the change in concentration of H2 in terms of x: -3x. Similarly, since two moles of NH3 are produced for every mole of N2 that reacts, we can write an expression for the change in concentration of NH3 in terms of x: +2x.
By setting up and solving the necessary equations, we can find the value of x and calculate the equilibrium concentrations of N2, H2, and NH3.
Defining the Ice Table
The ice table is a tool used in equilibrium calculations in chemistry. It is used to determine the concentrations of reactants and products in a chemical reaction, as well as the equilibrium constant for the reaction. The ice table gets its name from the fact that it is often used to track the changes in concentration of a chemical species as it goes from the initial to the final state, resembling the process of melting ice.
The ice table is typically set up by writing down the balanced chemical equation for the reaction and identifying the initial concentrations of all the reactants and products. Then, using stoichiometry and the concept of equilibrium, the changes in concentration of each species can be calculated. The ice table is organized in a tabular form, with rows representing the chemical species and columns representing the initial, change, and equilibrium concentrations.
Example:
Let’s consider the reaction:
2A + B ⇌ 3C
If the initial concentration of A is 0.2 M, B is 0.3 M, and C is 0.1 M, we can set up the ice table as follows:
| Chemical Species | Initial Concentration (M) | Change in Concentration (M) | Equilibrium Concentration (M) |
|---|---|---|---|
| A | 0.2 | -2x | 0.2 – 2x |
| B | 0.3 | -x | 0.3 – x |
| C | 0.1 | +3x | 0.1 + 3x |
Here, x represents the change in concentration of the reactants and products at equilibrium. By solving the equilibrium expression and making use of the values in the ice table, we can determine the value of x and find the concentrations of A, B, and C at equilibrium.
The ice table can be a useful tool for understanding and quantifying chemical reactions in equilibrium. It allows chemists to analyze the factors that affect the outcome of a reaction and predict how changes in conditions, such as temperature and pressure, will affect the equilibrium position.
Solving for Equilibrium Concentrations
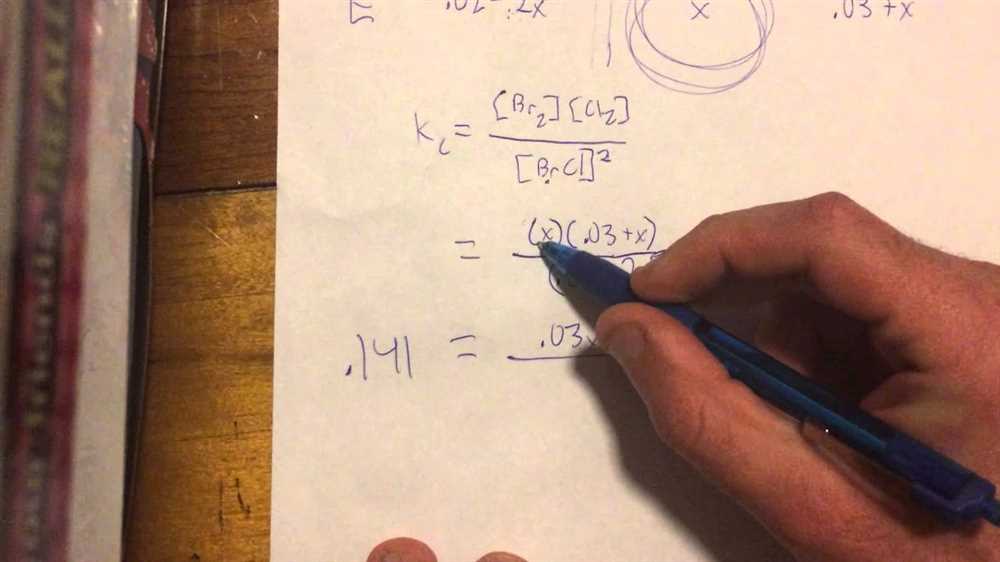
When studying chemical equilibrium, it is often necessary to calculate the equilibrium concentrations of various species in a reaction. This can be done using an ice table, which is a tool that organizes the information needed to solve for these concentrations. By following a set of steps and using the equilibrium constant expression, it is possible to solve for the unknowns.
The first step in solving for equilibrium concentrations is to write the balanced chemical equation for the reaction. This equation provides the stoichiometry of the reaction and helps determine the change in concentrations for each species. Once the equation is written, the initial concentrations of the reactants and products are identified.
Next, an ice table is constructed. The ice table is divided into three columns: one for the initial concentrations, one for the changes in concentrations, and one for the equilibrium concentrations. The initial concentrations are filled in for each species, and then the changes in concentrations are determined based on the stoichiometry of the reaction.
After the changes in concentrations are determined, the equilibrium concentrations can be calculated. This is done by subtracting the change in concentration from the initial concentration for each species. The equilibrium concentrations are then used to calculate the equilibrium constant for the reaction.
Using the equilibrium constant expression, it is possible to solve for the unknown equilibrium concentrations. This involves rearranging the equation and plugging in the known values, such as the equilibrium constant and the initial concentrations. By solving for the unknowns, the equilibrium concentrations of the species in the reaction can be determined.
In summary, solving for equilibrium concentrations involves writing the balanced chemical equation, constructing an ice table, determining the changes in concentrations, calculating the equilibrium concentrations, and using the equilibrium constant expression to solve for the unknowns. This process allows chemists to analyze and understand the behavior of reactions at equilibrium.
Calculating Kc from the Ice Table

The ice table is a useful tool in chemistry for calculating equilibrium concentrations and determining the equilibrium constant, Kc. By using the initial concentrations and the stoichiometry of the reaction, we can create an ice table to track the changes in concentrations at equilibrium.
First, let’s briefly review the steps for setting up an ice table:
- List the initial concentrations of the reactants and products.
- Identify the stoichiometry of the reaction to determine the change in concentration for each species.
- Set up the ice table with rows for each species and columns for initial concentration, change in concentration, and equilibrium concentration.
- Use the stoichiometry and the changes in concentration to fill in the ice table.
- Write the expression for the equilibrium constant, Kc, using the equilibrium concentrations.
- Solve for Kc by plugging in the known concentrations from the ice table.
Let’s consider an example to illustrate the process. Suppose we have the following reaction:
2A + 3B ⇌ 2C + D
If the initial concentrations are [A] = 0.25 M, [B] = 0.1 M, [C] = [D] = 0 M, and the equilibrium concentrations are [A] = 0.1 M, [B] = 0.05 M, [C] = 0.2 M, and [D] = 0.05 M, we can set up the ice table as follows:
| Species | Initial Concentration (M) | Change in Concentration (M) | Equilibrium Concentration (M) |
|---|---|---|---|
| A | 0.25 | -0.15 | 0.1 |
| B | 0.1 | -0.05 | 0.05 |
| C | 0 | 0.2 | 0.2 |
| D | 0 | 0.05 | 0.05 |
From the ice table, we can see that the equilibrium concentrations for A, B, C, and D are 0.1 M, 0.05 M, 0.2 M, and 0.05 M, respectively. Using these equilibrium concentrations, we can write the expression for Kc:
Kc = ([C]^2 * [D])/([A]^2 * [B]^3)
Substituting the values from the ice table, we can solve for Kc:
Kc = (0.2^2 * 0.05)/(0.1^2 * 0.05^3)
Kc = 8
Therefore, the equilibrium constant, Kc, for this reaction is 8.
By following these steps and properly setting up and filling in the ice table, we can accurately calculate the equilibrium constant, Kc, for a given reaction.
Determining the Equilibrium Constant Expression
In chemistry, the equilibrium constant (K) is a measure of the extent to which a reaction is favored in the direction of the products. It is an important concept in understanding chemical reactions and predicting their behavior. The equilibrium constant expression allows us to quantitatively describe the position of equilibrium.
To determine the equilibrium constant expression, we need to know the balanced chemical equation for the reaction. The equilibrium constant expression is defined as the ratio of the concentrations of the products raised to their stoichiometric coefficients divided by the concentrations of the reactants raised to their stoichiometric coefficients. Mathematically, it can be expressed as:
K = ([C]^c[D]^d) / ([A]^a[B]^b)
Where [A], [B], [C], and [D] are the concentrations of the reactants and products, and a, b, c, and d are their respective stoichiometric coefficients in the balanced chemical equation.
The equilibrium constant expression is dimensionless and does not depend on the initial concentrations of the reactants and products. It provides a way to determine the relative amounts of reactants and products at equilibrium, as well as predict the direction in which the reaction will proceed to reach equilibrium.
By calculating the equilibrium constant expression using experimental data, scientists can determine the value of K and gain insights into the thermodynamics and kinetics of the reaction. The equilibrium constant can also help in optimizing reaction conditions, designing new chemical processes, and understanding the factors that affect the position of equilibrium.
Adjusting Initial Concentrations
When working with ice table chemistry problems, it is common to need to adjust the initial concentrations of the chemical species involved. This is often necessary in order to accurately calculate the equilibrium concentrations and determine the values of the equilibrium constant.
One reason for adjusting the initial concentrations is to account for any reactants or products that may be present before the reaction begins. For example, if a reaction is taking place in a beaker that already contains some of the products, those initial concentrations need to be included in the calculations. This can be done by subtracting the initial concentrations of the products from the initial concentrations of the reactants.
Another reason for adjusting the initial concentrations is to ensure that the reaction is at its initial equilibrium state. In some cases, the reaction may not be at equilibrium initially due to factors such as temperature or pressure. In these cases, the initial concentrations can be adjusted to match the desired equilibrium conditions. This may involve adding or removing reactants or products to reach the desired initial equilibrium state.
Overall, adjusting the initial concentrations is an important step in solving ice table chemistry problems. It allows for accurate calculations of equilibrium concentrations and determination of equilibrium constants. By accounting for any reactants or products that may be present before the reaction begins, and ensuring that the reaction is at its initial equilibrium state, one can effectively solve these types of problems.
Changing Volume or Pressure
When dealing with chemical reactions, it is important to consider the impact that changes in volume or pressure can have on the equilibrium. These changes can affect the position of the equilibrium and ultimately the outcome of the reaction.
When the volume of a reaction system is changed, the concentration of the reactants and products can be altered. According to Le Chatelier’s principle, if the volume of a system is decreased, the equilibrium will shift in the direction that produces fewer moles of gas. Conversely, if the volume is increased, the equilibrium will shift in the direction that produces more moles of gas.
This principle also applies to changes in pressure. If the pressure of a reaction system is increased, the equilibrium will shift in the direction that produces fewer moles of gas, in order to decrease the pressure. On the other hand, if the pressure is decreased, the equilibrium will shift in the direction that produces more moles of gas, in order to increase the pressure.
It is important to note that changes in volume or pressure do not affect the value of the equilibrium constant (K), but rather the position of the equilibrium. The equilibrium constant remains the same as long as the temperature is constant.
- For example, consider the reaction:
2A + B ⇌ C + D
If the volume is decreased by halving it, the equilibrium will shift in the direction of fewer moles of gas, which is to the right. This means that the concentrations of C and D will increase, while the concentrations of A and B will decrease. Conversely, if the volume is doubled, the equilibrium will shift to the left, resulting in increased concentrations of A and B, and decreased concentrations of C and D.
Overall, understanding the impact that changes in volume or pressure can have on chemical equilibria is crucial for predicting and manipulating the outcomes of reactions.