
The mean score on a fitness exam is a crucial statistic that can provide valuable insights into the overall performance of individuals in a given population. By determining the average score, we can gain a better understanding of the level of fitness and physical abilities of the individuals taking the exam.
Estimating the mean score on a fitness exam requires a comprehensive and systematic approach. It involves collecting data from a representative sample of individuals who have taken the exam and analyzing it to determine the average score. This process helps to eliminate any potential bias and provides a more accurate picture of the overall performance.
Moreover, by estimating the mean score on a fitness exam, we can also compare the performance of different groups or populations. This can be particularly useful in identifying areas of improvement or disparities in fitness levels among individuals with different characteristics, such as age, gender, or ethnicity.
In conclusion, estimating the mean score on a fitness exam is a vital step in evaluating the performance of individuals and populations. It allows us to gain valuable insights into the overall fitness levels and physical abilities of individuals, identify areas of improvement, and make informed decisions regarding fitness programs and interventions.
The Importance of Estimating the Mean Score on a Fitness Exam

In the field of fitness, it is essential to accurately estimate the mean score on a fitness exam for various reasons. The mean score provides valuable insights into the performance of individuals or groups and helps in evaluating their overall fitness levels.
Assessment of Fitness Levels: Estimating the mean score on a fitness exam allows fitness professionals to assess the fitness levels of individuals or groups. By knowing the average performance, trainers can identify areas of improvement and develop targeted training programs to address specific weaknesses. This information helps in creating personalized workout plans and achieving optimal fitness results.
Comparison and Benchmarking: Estimating the mean score also enables comparison and benchmarking. It provides a standard against which the performance of individuals or groups can be assessed. Fitness professionals can compare different individuals or groups to see how they measure up in terms of fitness levels. This comparison can help identify outliers and set realistic goals for improvement.
Monitoring Progress and Goal Setting: Estimating the mean score on a fitness exam is crucial for monitoring progress and setting goals. By tracking the mean score over time, trainers can evaluate the effectiveness of training programs and make necessary adjustments. It also helps individuals to set realistic goals based on the average performance of others, ensuring they strive for achievable targets and continue to improve their fitness levels.
Identification of Strengths and Weaknesses: Estimating the mean score provides valuable insights into the strengths and weaknesses of individuals or groups. It helps trainers identify specific areas where individuals excel or struggle. With this information, trainers can tailor their training programs to focus on improving weak areas and further enhancing already strong areas.
Evidence-Based Decision Making: Estimating the mean score on a fitness exam allows for evidence-based decision making. By relying on statistical data, trainers and fitness professionals can make informed decisions regarding training strategies, program modifications, and performance evaluations. This data-driven approach ensures that decisions are objective, leading to more effective and efficient fitness training.
Methodology for Estimating the Mean Score
In estimating the mean score on a fitness exam, there are several steps that need to be followed to ensure accuracy and reliability. The first step is to randomly select a sample of individuals who have taken the fitness exam. This sample should be representative of the population to ensure that the estimated mean score is reflective of the entire population. Random selection helps to minimize bias and increase the validity of the estimate.
Once the sample has been selected, the next step is to calculate the mean score of the individuals in the sample. This is done by summing up all the individual scores and dividing the total by the number of individuals in the sample. The mean score is a measure of central tendency and provides an estimate of the average performance on the fitness exam.
In addition to calculating the mean score, it is also important to calculate a confidence interval. A confidence interval provides a range of values within which the true population mean score is likely to fall. The width of the confidence interval is determined by the level of confidence desired, with a higher level of confidence resulting in a wider interval. A common level of confidence is 95%, which means that there is a 95% probability that the true population mean score falls within the interval.
To calculate the confidence interval, the sample standard deviation and the sample size are needed. The sample standard deviation measures the spread or variability of the scores in the sample, while the sample size determines the precision of the estimate. Once these values are known, the confidence interval can be calculated using a statistical formula, such as the t-distribution or the z-distribution. The confidence interval provides a range of values that can be used to estimate the true population mean score with a specified level of confidence.
In summary, estimating the mean score on a fitness exam involves randomly selecting a representative sample, calculating the mean score of the sample, and determining a confidence interval. These steps help to ensure accuracy and provide a range of values within which the true population mean score is likely to fall.
Sample selection for estimating the mean score
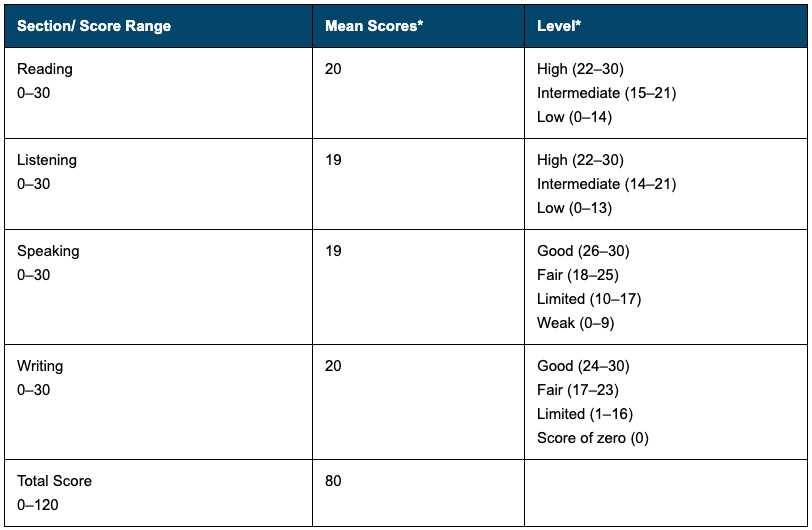
In order to accurately estimate the mean score on a fitness exam, it is essential to carefully select a representative sample of individuals. The sample must be chosen in a way that reflects the characteristics of the population being studied and minimizes any potential bias or confounding factors.
One common method for selecting a sample is through simple random sampling, where each individual in the population has an equal chance of being selected. This approach helps ensure that the sample is representative and unbiased. Another option is stratified sampling, where the population is divided into distinct groups or strata, and individuals are selected from each stratum in proportion to their representation in the population.
A key consideration in sample selection is the sample size. A larger sample size generally leads to more reliable estimates of the mean score. However, there is a trade-off between sample size and cost, as collecting data from a larger sample can be time-consuming and expensive. It is important to strike a balance between the desired precision of the estimate and the available resources.
In addition to the selection method and sample size, it is crucial to ensure the sample is truly representative of the population. This can be achieved by employing techniques such as stratified random sampling or cluster sampling, where certain demographic characteristics or geographic areas are specifically targeted. By including individuals from diverse backgrounds and locations, the estimated mean score will be more robust and applicable to the entire population.
In summary, the process of sample selection for estimating the mean score on a fitness exam involves careful consideration of the selection method, sample size, and representativeness of the sample. By choosing a representative sample using appropriate sampling techniques, the estimated mean score will be more accurate and reliable for making inferences about the entire population.
Data collection for estimating the mean score on a fitness exam
Collecting accurate and representative data is crucial in estimating the mean score on a fitness exam. To ensure the reliability of the estimation, it is important to use proper sampling techniques and gather a diverse sample of individuals. The sample should be selected randomly from the target population to minimize bias and ensure that the results can be generalized to the entire population. One possible approach is to use a simple random sampling method where each individual has an equal chance of being selected.
Once the sample has been selected, it is essential to collect data on the fitness exam scores in a systematic and consistent manner. Standardized tests or assessments can be utilized to ensure that all participants are evaluated using the same criteria. This helps to eliminate any potential confounding variables and allows for a fair and accurate comparison of scores. It is also important to ensure that the data collection process is well-documented and that any relevant information about the participants, such as age, gender, or fitness level, is recorded.
In addition to the actual fitness exam scores, it may also be useful to collect additional data that could potentially impact the mean score estimation. This could include information on the participants’ exercise habits, dietary patterns, or previous experience with fitness exams. By collecting this supplementary data, researchers can gain a deeper understanding of the factors that contribute to performance on the exam and how they may influence the overall mean score.
Key steps for data collection:
- Select a sample randomly from the target population using a simple random sampling method.
- Use standardized tests or assessments to evaluate participants’ fitness exam scores.
- Ensure consistent and systematic data collection.
- Record relevant participant information, such as age, gender, and fitness level.
- Consider collecting additional data on factors that may impact the mean score estimation.
By following these steps and implementing rigorous data collection procedures, researchers can obtain reliable and accurate estimates of the mean score on a fitness exam. This information can then be used to make informed decisions about fitness program effectiveness, identify areas for improvement, and tailor interventions to better meet the needs of the population.
Statistical analysis for estimating the mean score

Estimating the mean score on a fitness exam requires careful statistical analysis to ensure accuracy and reliability. One commonly used method is to take a random sample of individuals who have completed the exam and calculate the mean score based on their results. This approach allows us to make inferences about the population mean score with a certain level of confidence.
To begin the analysis, we need to determine the appropriate sample size. This is crucial in order to minimize sampling error and obtain a representative sample. The sample size can be calculated using statistical formulas, taking into account factors such as desired margin of error, confidence level, and variability in the population.
Once the sample size is determined, the next step is to randomly select individuals from the population who have taken the fitness exam. This random sampling helps to ensure that the sample is representative of the entire population and reduces the risk of bias. It is important to note that the larger the sample size, the more accurate our estimate of the population mean score will be.
After the sample is selected, we can calculate the mean score based on the scores of the individuals in the sample. This provides an estimate of the population mean score. In addition to the mean score, it is also important to calculate measures of variability, such as standard deviation or confidence intervals. These measures provide information about the spread or dispersion of the scores and can help to assess the reliability of our estimate.
To further validate our estimate, hypothesis testing can be conducted. This involves comparing the estimated mean score to a hypothesized value using statistical tests. The results of these tests will determine whether the estimated mean score is significantly different from the hypothesized value, providing evidence for or against certain claims or hypotheses.
Factors affecting the estimation of the mean score
The estimation of the mean score on a fitness exam can be influenced by several factors that need to be taken into consideration. Firstly, the sample size of the population being examined plays a crucial role. A larger sample size tends to provide a more accurate estimate of the mean score, as it reduces the potential impact of outliers or extreme values. Conversely, a smaller sample size can lead to a less reliable estimation of the mean, making it important to ensure an adequate representation of the population in the sample.
Another factor that affects the estimation of the mean score is the variability within the population. If the population being examined is highly diverse in terms of fitness levels, the estimation of the mean score may be more challenging. In such cases, it becomes important to consider stratified sampling techniques that ensure proportional representation of different subgroups within the population.
Additionally, the presence of any biases in the sample selection process can affect the estimation of the mean score. If the sample is not randomly selected or does not accurately represent the population, the estimated mean score may be biased and not reflect the true population mean. It is therefore crucial to ensure that the sampling process is unbiased and that appropriate methods are used to correct any potential biases.
Furthermore, the accuracy of the measurement instrument used to assess fitness levels is another important factor that affects the estimation of the mean score. If the instrument is not reliable or valid, the estimated mean score may be misleading. It is essential to use standardized and validated measurement tools to ensure the accuracy and consistency of the data collected.
In conclusion, the estimation of the mean score on a fitness exam is influenced by factors such as the sample size, variability within the population, sample selection biases, and the accuracy of the measurement instrument. By taking these factors into consideration and implementing appropriate sampling and measurement techniques, a more accurate estimation of the mean score can be obtained, providing valuable insights into the fitness levels of the population under study.