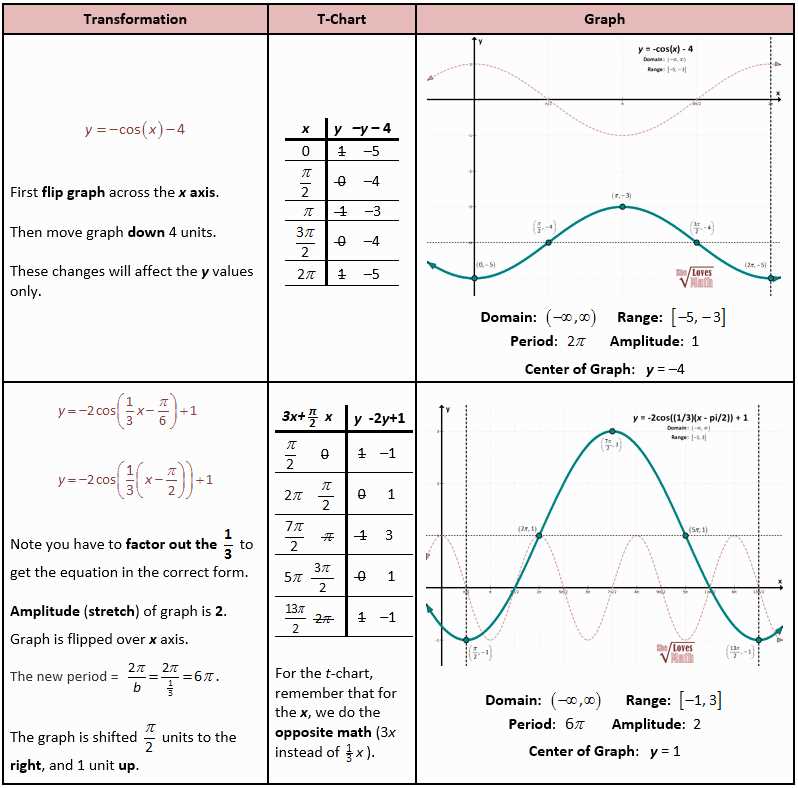
In mathematics, trigonometry is a branch that deals with the relationships between the angles and sides of triangles. It has wide applications in various fields, including physics, engineering, and navigation. To master this important branch of mathematics, students often practice solving trigonometry problems using worksheets. However, without the correct answers, it can be challenging to gauge one’s progress and identify areas that need improvement.
This article aims to provide an introduction to trigonometry worksheet answers, offering solutions to commonly encountered problems. By having access to these answers, students can confirm their calculations, identify any errors, and gain a deeper understanding of the concepts. Each answer will be explained step-by-step, ensuring a comprehensive grasp of the underlying principles.
The worksheet answers will cover fundamental trigonometric concepts, such as the sine, cosine, and tangent functions, as well as solving right triangles using trigonometric ratios. Through these answers, students can develop the necessary skills to solve more complex problems, including applications of trigonometry in real-life scenarios. With practice and a thorough understanding of the answers provided, students will be well-equipped to tackle more advanced topics in trigonometry.
Exploring Basic Trigonometric Principles
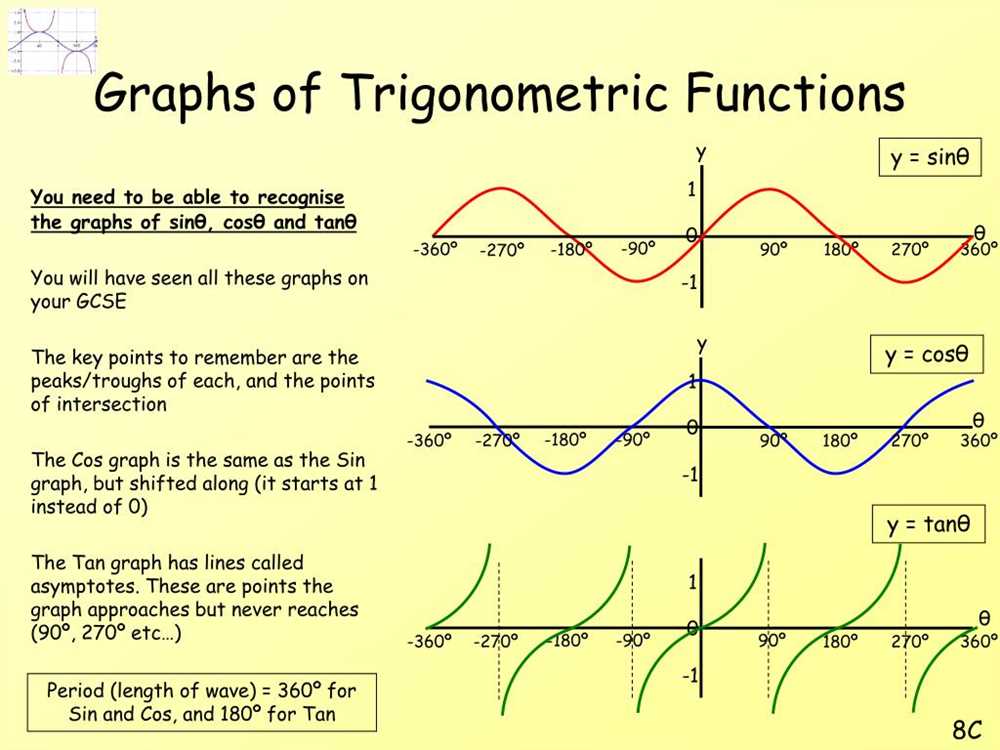
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is widely used in various fields such as engineering, physics, and navigation. In this worksheet, we will be exploring some basic trigonometric principles and their applications.
Right Triangle Trigonometry
One of the fundamental concepts in trigonometry is right triangle trigonometry, which involves the study of right triangles. A right triangle is a triangle with one angle measuring 90 degrees. The sides of a right triangle are called the hypotenuse, adjacent side, and opposite side. The relationships between these sides and the angles of the triangle can be described using trigonometric functions.
- Sine (sin): The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is often used to solve problems involving the height of an object or the distance between two objects.
- Cosine (cos): The cosine of an angle in a right triangle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. It is commonly used to solve problems involving the length of a side of a triangle.
- Tangent (tan): The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. It is often used to solve problems involving the slope of a line or the angle of elevation or depression.
Applications of Trigonometry
Trigonometry is not just a theoretical branch of mathematics, but it also has numerous practical applications. It is used in navigation to determine distances and bearings between two points. It is used in architecture and engineering to calculate the angles and dimensions of structures. Trigonometry is also used in physics to analyze the motion of objects and in computer graphics to create realistic 3D images.
In conclusion, trigonometry is a powerful tool that helps us understand and solve problems involving angles and sides of triangles. By learning and applying basic trigonometric principles, we can gain valuable insights and solve real-world problems more efficiently.
Solving Simple Trigonometric Equations

Trigonometric equations involve the use of trigonometric functions such as sine, cosine, and tangent, and can be solved by applying algebraic techniques. These equations often arise in various fields of mathematics and physics, and it is important to understand how to solve them in order to find the solutions.
A simple trigonometric equation typically involves a single trigonometric function and asks for values of the unknown angle that satisfy the equation. The first step in solving such an equation is to isolate the trigonometric function by moving any constant terms to the other side of the equation and applying algebraic operations. Once the trigonometric function is isolated, trigonometric identities and properties can be used to simplify the equation and find the solutions.
For example, let’s say we have the equation sin(x) = 0.5. To solve this equation, we can use the inverse sine function, also known as arcsin, to find the values of x. By taking the inverse sine of both sides of the equation, we get x = arcsin(0.5). Calculating the inverse sine of 0.5 using a calculator or reference table, we find that x = 30 degrees or x = π/6 radians. These are the solutions to the equation sin(x) = 0.5.
In summary, solving simple trigonometric equations involves isolating the trigonometric function, applying trigonometric identities and properties, and using inverse trigonometric functions to find the solutions. It is important to understand these techniques in order to solve various trigonometric equations that arise in mathematical and scientific contexts.
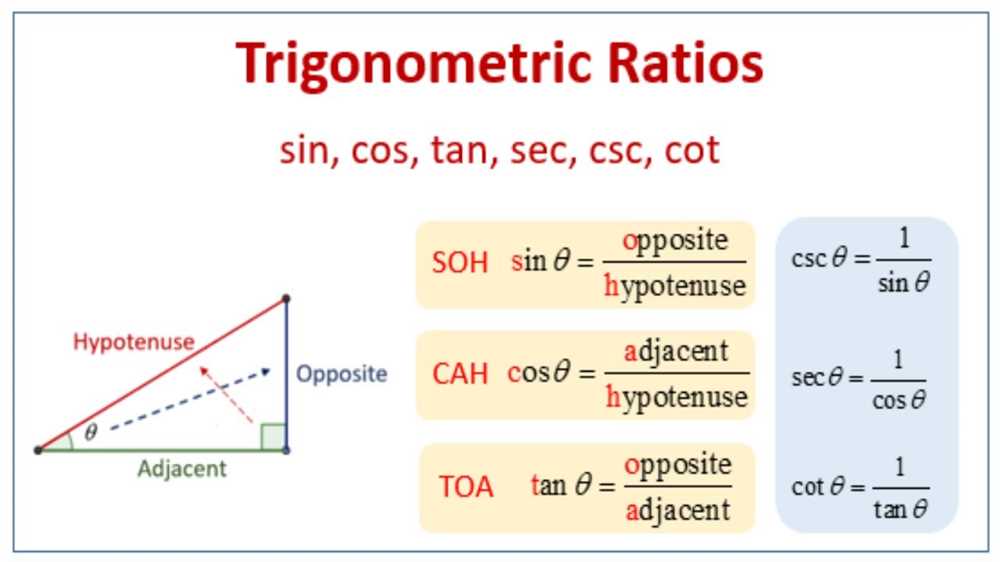
Understanding Trigonometric Ratios
Trigonometric ratios are mathematical functions that relate the angles of a right triangle to the ratios of the lengths of its sides. These ratios are widely used in various fields such as physics, engineering, and navigation. Understanding trigonometric ratios is essential for solving problems involving angles and distances.
Sine: The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is denoted by sin(theta) or sin(theta) = opposite/hypotenuse.
Cosine: The cosine of an angle in a right triangle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. It is denoted by cos(theta) or cos(theta) = adjacent/hypotenuse.
Tangent: The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. It is denoted by tan(theta) or tan(theta) = opposite/adjacent.
These trigonometric ratios can be used to find missing angles or side lengths in a right triangle. By knowing the values of two sides or one side and one angle, we can use trigonometric functions to calculate the missing information.
Trigonometric ratios are also used to represent periodic phenomena such as waves and oscillations. They help describe the relationship between the angle and the value of the function at that angle, enabling us to analyze and predict the behavior of such phenomena.
Summary:
- Sine is the ratio of the side opposite the angle to the hypotenuse.
- Cosine is the ratio of the side adjacent to the angle to the hypotenuse.
- Tangent is the ratio of the side opposite the angle to the side adjacent to the angle.
Understanding and applying trigonometric ratios is crucial for solving a wide range of problems in mathematics and various scientific fields.
Applying Trigonometry to Real-World Scenarios
Trigonometry is more than just a theoretical branch of mathematics. It has numerous practical applications in real-world scenarios, where it is used to solve problems related to angles, distances, heights, and other geometric measurements. By understanding trigonometric concepts and formulas, individuals can analyze and solve various real-life problems, making trigonometry an essential skill in fields such as engineering, architecture, navigation, and physics.
One common application of trigonometry is in surveying land. Surveyors use trigonometric principles to measure distances, angles, and heights, allowing them to create accurate maps and determine the boundaries of properties. By measuring angles and using trigonometric ratios such as sine, cosine, and tangent, surveyors can calculate the length of inaccessible sides of a triangle or the height of a tall building.
Trigonometry also plays a crucial role in navigation, particularly for pilots and sailors. By using the principles of trigonometry, they can determine their position, speed, and direction of travel. For example, using the concept of bearing and trigonometric ratios, pilots can calculate their true heading and the distance between two points. Likewise, sailors can use trigonometry to plot their course and determine the distance between two ships.
Another practical application of trigonometry is found in the field of physics. Many physical phenomena, such as waves, vibrations, and circular motion, can be described and analyzed using trigonometric functions. These functions help scientists and engineers understand the behavior of objects in motion and the relationship between variables such as frequency, amplitude, and phase angle.
In conclusion, trigonometry is not just an abstract mathematical concept but a valuable tool for solving real-world problems. Its applications in surveying, navigation, and physics demonstrate its importance in various fields. By mastering trigonometric principles and formulas, individuals can analyze and interpret the geometric properties of objects and phenomena, enabling them to make informed decisions and solve complex problems.
Working with Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. These functions, such as sine, cosine, and tangent, are essential in the field of trigonometry and have applications in various areas, such as physics, engineering, and geometry.
Sine is the ratio of the length of the side opposite an angle to the hypotenuse of the triangle. It is denoted by the symbol sin and can be calculated using the formula sin(theta) = opposite/hypotenuse.
Cosine is the ratio of the length of the adjacent side to the hypotenuse of the triangle. It is denoted by the symbol cos and can be calculated using the formula cos(theta) = adjacent/hypotenuse.
Tangent is the ratio of the length of the side opposite an angle to the length of the adjacent side. It is denoted by the symbol tan and can be calculated using the formula tan(theta) = opposite/adjacent.
These trigonometric functions can be used to solve problems involving angles and lengths of sides in triangles. They allow us to find missing angles or sides given certain information, and they also enable us to analyze and understand the relationships between angles and sides in various geometrical situations.
It is important to have a solid understanding of trigonometric functions, as they form the foundation for more advanced concepts in trigonometry and are widely used in real-world applications. By practicing and working with trigonometric functions, you can develop the skills necessary to solve complex problems and make accurate calculations in various fields.
Evaluating Trigonometric Identities
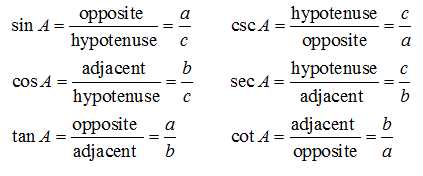
Trigonometric identities play a crucial role in solving trigonometric equations and problems. Evaluating trigonometric identities involves manipulating the given expressions to simplify them or prove their equality. By applying different trigonometric identities, such as the Pythagorean identities, reciprocal identities, and quotient identities, we can determine the values of trigonometric functions for given angles.
One common method for evaluating trigonometric identities is by using algebraic manipulation and substitution. For example, we can use the Pythagorean identities to simplify a trigonometric expression or equation. The Pythagorean identity states that sin²θ + cos²θ = 1. By substituting this identity into a given expression, we can simplify it and potentially find a simpler form.
Another approach to evaluating trigonometric identities is by using the fundamental trigonometric identities. These identities involve the sine, cosine, and tangent functions, as well as their reciprocals and inverses. By applying these identities, we can simplify or prove the equality of trigonometric expressions.
To effectively evaluate trigonometric identities, it is important to have a good understanding of the properties and relationships between trigonometric functions. Practice and familiarity with various trigonometric identities will allow for easier manipulation and evaluation of trigonometric expressions.
Examples:
- Evaluating sin(π/4)
- Simplifying (secθ)/(1+tanθ)
- Proving cos²θ + sin²θ = 1
By using the appropriate trigonometric identity and applying algebraic manipulation, we can find the solutions to these examples and evaluate trigonometric identities in a variety of contexts.
Applying Trigonometry to Right Triangles
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. One of the key applications of trigonometry is in solving problems involving right triangles. In a right triangle, one of the angles is 90 degrees, which makes it a special case for trigonometric calculations.
One of the fundamental trigonometric ratios used in right triangles is the sine function. The sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. This can be represented as sin(theta) = opposite/hypotenuse. Similarly, the cosine function relates the adjacent side to the hypotenuse, and the tangent function relates the opposite side to the adjacent side.
By knowing the lengths of two sides of a right triangle, or by knowing the length of one side and the measure of one angle, we can use trigonometric functions to find the lengths of other sides or the measure of other angles. This is particularly useful in real-world applications such as navigation, engineering, and physics.
When working with right triangles, it is important to keep in mind the concept of similar triangles. Similar triangles have the same shape but may differ in size. This property allows us to use trigonometry to solve problems involving triangles that are not necessarily right triangles, by recognizing the relationships between corresponding angles and sides.
In summary, applying trigonometry to right triangles involves using the trigonometric ratios to find missing side lengths or angles. This can be done by identifying the given information and applying the appropriate trigonometric function. Understanding the concepts of similar triangles can also be helpful in solving more complex trigonometry problems. Trigonometry is a powerful tool that has many applications in various fields, and mastering its principles can greatly expand your problem-solving skills.