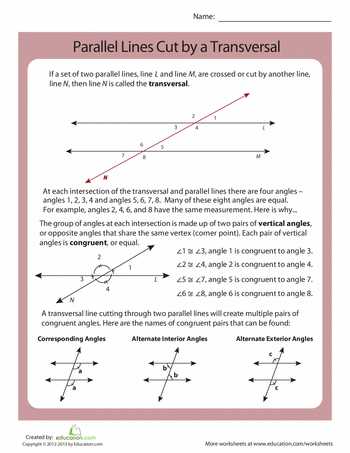
In geometry, parallel lines have always been a fascinating topic to explore. When a transversal line intersects parallel lines, various angles are formed, and it becomes crucial to understand their properties and relationships. In this article, we will delve into the answer key of lesson 11.1 on parallel lines cut by a transversal.
By studying this answer key, students will gain a deep understanding of the different types of angles formed by the intersection of transversals with parallel lines. They will also learn how to identify and classify these angles, such as corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.
This answer key will provide students with the necessary tools to solve problems involving parallel lines and transversals. They will be able to apply the properties of these angles to find missing angle measures, prove angle relationships, and make conclusions about the parallel lines and transversals.
Lesson 11 1 Parallel Lines Cut by a Transversal Answer Key

In Lesson 11.1, we explored the concept of parallel lines being intersected by a transversal. This lesson helps us understand the relationships between the angles formed when parallel lines are intersected by a transversal. By using the answer key provided, we can check and verify our understanding of these angle relationships.
The answer key for Lesson 11.1 Parallel Lines Cut by a Transversal provides us with the correct angle measurements for various pairs of angles formed by the transversal. This allows us to compare our own measurements and calculations to the correct answers, helping us to identify any errors or misconceptions we may have.
The answer key not only gives us the correct angle measurements, but it also explains the reasoning behind these measurements. It shows us how to identify corresponding angles, alternate interior angles, alternate exterior angles, consecutive interior angles, and vertical angles. By understanding these angle relationships, we can apply them to solve problems and prove different properties of parallel lines cut by a transversal.
Using the Answer Key
To use the Lesson 11.1 Parallel Lines Cut by a Transversal Answer Key effectively, it is important to carefully compare our own measurements and calculations to the correct answers provided. If our measurements match the answers, we can be confident in our understanding of the angle relationships. However, if our measurements are different, we should carefully review our work and identify any errors we may have made.
The answer key also includes explanations and diagrams to help clarify the angle relationships. It is important to carefully study these explanations to further enhance our understanding of the topic. By actively engaging with the answer key and seeking to understand the reasoning behind the correct answers, we can deepen our knowledge and improve our problem-solving skills.
Understanding Parallel Lines
Parallel lines are a fundamental concept in geometry. They are lines that are always equidistant and never intersect. Understanding parallel lines is important because they play a significant role in various mathematical concepts, such as angles, triangles, and quadrilaterals.
One way to identify parallel lines is by looking for a transversal line that intersects two or more lines at different points. The angles formed by the transversal and the parallel lines are known as corresponding, alternate interior, alternate exterior, or consecutive interior angles. These angles have specific properties and relationships that help us analyze and solve geometric problems.
For example, corresponding angles are congruent when a transversal intersects two parallel lines. This property allows us to determine angle measurements and find missing angles in geometric figures. Similarly, alternate interior angles are congruent, and alternate exterior angles are congruent. These relationships enable us to establish various properties and solve complex geometric problems.
Moreover, parallel lines also help us understand the properties of triangles and quadrilaterals. For instance, if a transversal intersects two parallel lines, it creates a series of congruent or proportional segments within the triangles formed. This leads to the development of similar triangles or enables us to find the lengths of sides in different quadrilaterals.
Overall, having a solid understanding of parallel lines allows us to analyze and solve various geometric problems. It provides us with the necessary tools to explore angles, triangles, and quadrilaterals, and make connections between different geometric concepts.
Identifying Transversals

When studying parallel lines and their properties, one important concept to understand is that of transversals. A transversal is a line that intersects two or more parallel lines, creating multiple angles and relationships between the lines. By identifying and understanding these transversals, we can unlock a deeper understanding of the geometry of parallel lines.
To identify a transversal, we first need to identify the parallel lines that it intersects. Parallel lines are two or more lines that never intersect and are always equidistant from each other. Once we have identified the parallel lines, we can then look for a line that intersects them. This line is the transversal.
When a transversal intersects parallel lines, it creates a variety of angles that have special properties. Some of the key terms to know when studying transversals are corresponding angles, alternate interior angles, alternate exterior angles, consecutive interior angles, and consecutive exterior angles. By understanding the relationships between these angles, we can solve for missing angles, prove theorems, and make connections between different geometric concepts.
Corresponding Angles:
- Corresponding angles are angles that are in the same position relative to the transversal and the parallel lines. They are on the same side of the transversal and in corresponding positions.
- Corresponding angles are always congruent if the lines that the transversal intersects are parallel.
Alternate Interior Angles:
- Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate interior angles are always congruent if the lines that the transversal intersects are parallel.
Alternate Exterior Angles:
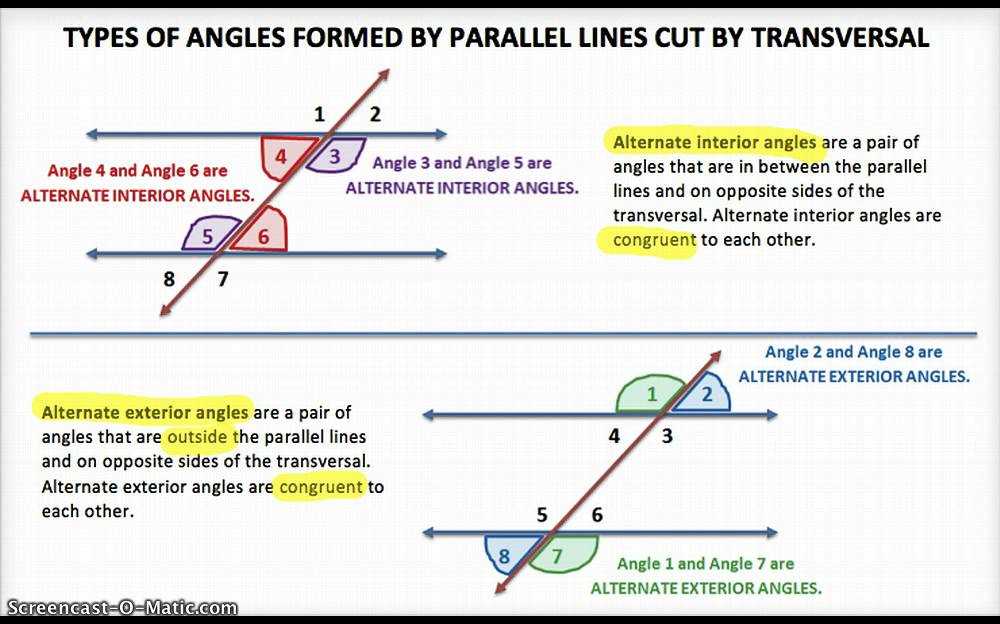
- Alternate exterior angles are angles that are on opposite sides of the transversal and outside the parallel lines.
- Alternate exterior angles are always congruent if the lines that the transversal intersects are parallel.
By understanding the properties and relationships of transversals, we can solve for missing angles, prove geometric theorems, and make connections to other areas of mathematics and real-world applications. Identifying transversals is a fundamental skill when studying parallel lines, and it is crucial for success in advanced geometry and beyond.
Angle Relationships
In geometry, angle relationships refer to the relationships between two or more angles in a given figure. Understanding these relationships is crucial in solving problems involving angles, lines, and shapes.
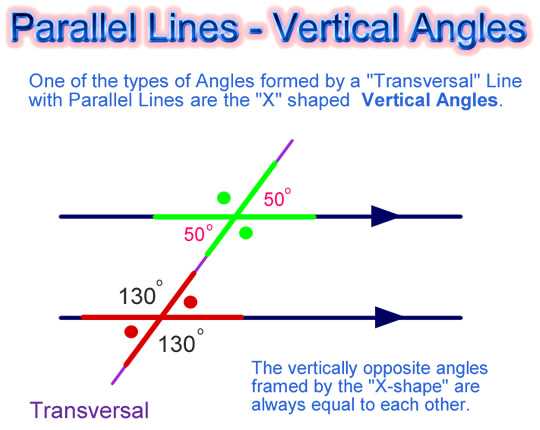
One common type of angle relationship is a vertical angle. Vertical angles are formed when two lines intersect. These angles are always congruent, meaning they have the same measure. For example, if angle A and angle B are vertical angles, then angle A = angle B.
Another important angle relationship is a linear pair. A linear pair consists of two adjacent angles whose measures add up to 180 degrees. For example, if angle C and angle D are a linear pair, then angle C + angle D = 180 degrees.
Parallel lines and a transversal also create several angle relationships. When a transversal intersects two parallel lines, corresponding angles are congruent, alternate interior angles are congruent, and alternate exterior angles are congruent. For example, if line AB is parallel to line CD and transversal EF intersects them, then angle 1 = angle 5 (corresponding angles), angle 3 = angle 6 (alternate interior angles), and angle 2 = angle 8 (alternate exterior angles).
Understanding angle relationships allows us to find missing angle measures, solve equations involving angles, and prove geometric theorems. It provides a foundation for further study in geometry and helps us analyze and make sense of the angles and shapes around us.
Summary:
- Angle relationships refer to the relationships between two or more angles in a figure.
- Vertical angles are congruent.
- A linear pair consists of two adjacent angles whose measures add up to 180 degrees.
- Corresponding angles, alternate interior angles, and alternate exterior angles are congruent when a transversal intersects two parallel lines.
- Understanding angle relationships helps solve problems and analyze geometric figures.
Corresponding Angles
When two parallel lines are intersected by a transversal, corresponding angles are formed. Corresponding angles are pairs of angles that are in the same position relative to the transversal and the parallel lines.
The corresponding angles are congruent, which means they have the same measure. In other words, if ∠1 and ∠5 are corresponding angles, then the measure of ∠1 is equal to the measure of ∠5. Similarly, if ∠2 and ∠6 are corresponding angles, then the measure of ∠2 is equal to the measure of ∠6.
Corresponding angles can be found on the same side of the transversal or on opposite sides of the transversal. For example, in the diagram below, ∠1 and ∠5 are corresponding angles on the same side of the transversal, and ∠2 and ∠6 are corresponding angles on opposite sides of the transversal.
- ∠1 and ∠5 are corresponding angles, and they are congruent.
- ∠2 and ∠6 are corresponding angles, and they are congruent.
- ∠3 and ∠7 are corresponding angles, and they are congruent.
- ∠4 and ∠8 are corresponding angles, and they are congruent.
Understanding corresponding angles is important when working with parallel lines and transversals, as it helps in solving problems involving angles and their relationships in geometric figures.
Alternate Interior Angles
Alternate interior angles are a pair of angles that are formed on opposite sides of a transversal line when two parallel lines are intersected by the transversal. These angles are congruent, which means they have the same measure.
To better understand alternate interior angles, let’s consider a diagram with two parallel lines, labeled as line a and line b, and a transversal line, labeled as line t. When line t intersects lines a and b, it forms several pairs of angles. Among these pairs are the alternate interior angles.
- Angle 1: formed on the inside of the parallel lines and above line t.
- Angle 4: formed on the inside of the parallel lines and below line t.
These angles have the same measure and can be represented as angle 1 ≅ angle 4. In other words, if angle 1 measures 70 degrees, angle 4 would also measure 70 degrees.
Alternate interior angles are important in geometry because they can help us prove various theorems and solve problems involving parallel lines and transversals. By knowing that these angles are congruent, we can use this information to find missing angles, solve equations, and make geometric constructions.
Alternate Exterior Angles
Alternate exterior angles are pairs of angles that are formed when a transversal intersects two parallel lines. They are located on opposite sides of the transversal and are exterior to the parallel lines. When parallel lines are cut by a transversal, alternate exterior angles are always congruent.
Alternate exterior angles can be identified by their positions. They are located on different sides of the transversal and are not adjacent to each other. They form a “z” shape or a “C” shape when the parallel lines are extended. The angles that are on the same side of the transversal and on the same side of the parallel lines are called alternate interior angles.
Alternate exterior angles have several important properties. First, they are congruent. This means that if two parallel lines are cut by a transversal, then the alternate exterior angles formed are equal in measure. Second, they are supplementary to each other. This means that the sum of the measures of two alternate exterior angles is equal to 180 degrees.
Knowing the properties of alternate exterior angles can help in solving various geometric problems. For example, if a pair of alternate exterior angles is given, their measures can be used to find the measures of other angles in the figure. Additionally, the congruence of alternate exterior angles can be used to prove that two lines are parallel, by applying the converse of the Alternate Exterior Angles Theorem.
In conclusion, alternate exterior angles are pairs of congruent angles that are formed when a transversal intersects two parallel lines. They have specific positions and properties, and can be used in solving geometric problems and proving theorems.
Consecutive Interior Angles
Consecutive interior angles are angles that are formed when a transversal intersects two parallel lines. These angles are located on the same side of the transversal and are inside the parallel lines. Consecutive interior angles are also known as same-side interior angles. They are named “consecutive” because they appear one after another as you move from one side of the transversal to the other.
The sum of consecutive interior angles is always equal to 180 degrees. This is a property that holds true for any pair of parallel lines and any transversal that intersects them. The sum of the measures of the consecutive interior angles can be used to determine the measure of an unknown angle if the value of one angle is known.
Consecutive interior angles can be used to solve various types of problems involving parallel lines and transversals. For example, they can be used to find missing angle measures, prove geometric theorems, or establish congruence between angles. Understanding the properties and relationships of consecutive interior angles is essential in geometry.
Properties of Consecutive Interior Angles:
- They are located on the same side of the transversal.
- They are inside the parallel lines.
- The sum of their measures is always 180 degrees.
- They can be used to find missing angle measures.
- They can be used to prove geometric theorems.
- They can establish congruence between angles.
Overall, consecutive interior angles play a significant role in the study of parallel lines and transversals. Their properties and relationships provide valuable information that can be used to solve various geometric problems. By understanding the concept of consecutive interior angles, one can gain a deeper understanding of the connections between angles and parallel lines.