
In this article, we will provide the answer key for the practice problems in Lesson 12. These practice problems were designed to test your understanding of the material covered in the lesson and help reinforce the concepts learned.
Throughout the practice problems, you were asked a series of questions and given multiple choice options to choose from. In this answer key, we will provide the correct answers for each question and explain the reasoning behind them.
By reviewing this answer key, you can compare your answers to the correct ones and assess your understanding of the lesson. This will help you identify any areas where you may need further clarification or practice, allowing you to strengthen your knowledge and improve your skills.
Lesson 12 Practice Problems Answer Key
Below is the answer key for the practice problems in Lesson 12. Use the answers to check your work and understand the concepts better.
1. Question: What is the capital city of France?
| Answer: | Paris |
|---|
2. Question: Solve the equation 3x + 2 = 8.
| Answer: | x = 2 |
|---|
3. Question: List the first five elements of the periodic table.
| Answer: |
|
|---|
4. Question: Name three famous painters from the Renaissance period.
| Answer: |
|
|---|
5. Question: Calculate the area of a rectangle with length 6 cm and width 4 cm.
| Answer: | Area = 24 cm2 |
|---|
These are the answers to the practice problems in Lesson 12. Make sure to review them and understand the concepts thoroughly.
Problem 1: Solve a Linear Equation
Linear equations are a fundamental concept in algebra and solving them is an important skill to have. In this problem, we will focus on solving a simple linear equation. The equation we need to solve is:
2x + 5 = 13
To solve this equation, we want to isolate the variable x on one side of the equation. We can do this by performing inverse operations.
First, we can subtract 5 from both sides of the equation to get:
2x = 8
Next, we want to isolate x by dividing both sides of the equation by 2:
x = 4
Therefore, the solution to the given linear equation is x = 4. This means that substituting x with 4 in the original equation will make it a true statement:
2(4) + 5 = 13
Which simplifies to:
8 + 5 = 13
And indeed, 13 is equal to 13, confirming that our solution is correct.
Problem 2: Find the Gradient of a Function
In mathematics, the gradient of a function is a measure of how steep the function is at any given point. It represents the rate of change of the function with respect to its variables. The gradient is a vector that points in the direction of the steepest increase of the function and its magnitude indicates the steepness of the increase.
The gradient of a function can be found using calculus. For a function of multiple variables, such as f(x, y, z), the gradient is calculated by taking the partial derivative of the function with respect to each variable. The partial derivative measures the rate of change of the function with respect to one variable while holding the other variables constant.
To find the gradient of a function, we first need to determine the partial derivatives of the function with respect to each variable. These partial derivatives can then be combined into a vector called the gradient vector. The gradient vector will have the same number of components as the number of variables in the function, and each component represents the rate of change of the function with respect to its corresponding variable.
The gradient is an important concept in optimization and calculus. It allows us to determine the direction in which a function is changing the fastest, which can be useful in finding the maximum or minimum values of a function. The gradient is also used in physics to represent the direction of maximum increase of a scalar field, such as temperature or pressure.
In summary, the gradient of a function measures its steepness and direction of change. It can be found by taking the partial derivatives of the function with respect to its variables. The gradient is a vector that points in the direction of steepest increase and its magnitude represents the rate of change of the function. The gradient is a powerful tool in optimization and calculus.
Problem 3: Calculate the Area of a Triangle

In this problem, we are tasked with calculating the area of a triangle. To do this, we can use the formula for the area of a triangle, which is Area = (base * height) / 2.
First, we need to determine the base and height of the triangle. The base is one of the sides of the triangle, while the height is the perpendicular distance from the base to the opposite vertex.
| Given: | Base = 5 cm |
| Height = 8 cm |
Using the given values, we can calculate the area of the triangle as follows:
Area = (5 cm * 8 cm) / 2 = 40 cm2
Therefore, the area of the triangle is 40 square centimeters.
Problem 4: Determine the Probability of an Event
In this problem, we are tasked with determining the probability of a specific event occurring. Probability is a measure of the likelihood or chance that an event will occur. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to happen.
To calculate the probability of an event, we need to consider the number of favorable outcomes and the total number of possible outcomes. The probability of the event is then obtained by dividing the number of favorable outcomes by the total number of possible outcomes.
For example, let’s say we have a bag of 20 marbles, consisting of 15 red marbles and 5 blue marbles. If we randomly select a marble from the bag, the probability of selecting a red marble would be calculated as follows:
P(Red Marble) = Number of favorable outcomes / Total number of possible outcomes
In this case, the number of favorable outcomes is 15 (the number of red marbles) and the total number of possible outcomes is 20 (the total number of marbles in the bag). By dividing 15 by 20, we find that the probability of selecting a red marble is 0.75 or 75%.
Probability is an important concept in statistics and is used in various fields, such as business, sports, and science, to make predictions and informed decisions. By understanding the probability of an event, we can assess the likelihood of its occurrence and make more informed choices.
Problem 5: Evaluate an Algebraic Expression
In this problem, we are given an algebraic expression and we need to evaluate it. An algebraic expression consists of variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. To evaluate an expression, we substitute the values of variables and perform the indicated operations.
For example, let’s consider the expression 3x + 4y – 2z, where x, y, and z are variables. To evaluate this expression, we need to know the values of x, y, and z. Once we have the values, we can substitute them into the expression and perform the operations. For instance, if x = 2, y = 5, and z = 1, the expression becomes:
3(2) + 4(5) – 2(1) = 6 + 20 – 2 = 24.
Therefore, when x = 2, y = 5, and z = 1, the value of the expression 3x + 4y – 2z is 24.
Problem 6: Convert Units of Measurement
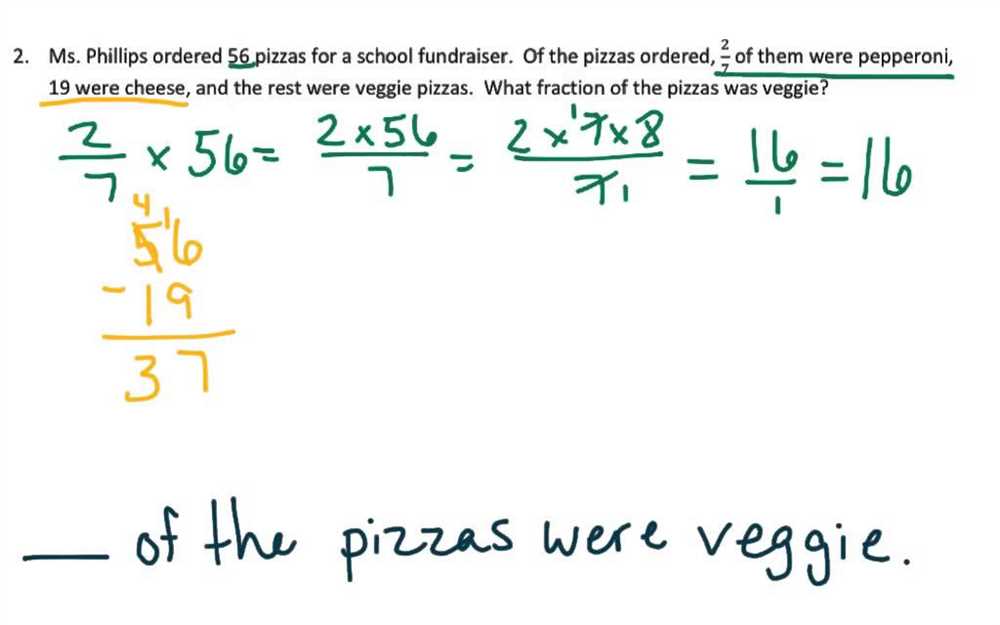
In problem 6, we are given a measurement in one unit and asked to convert it to another unit. This problem requires us to understand the conversion factors between different units of measurement.
In this problem, we are given a length measurement in centimeters and we need to convert it to millimeters. To do this, we need to know that there are 10 millimeters in 1 centimeter. Therefore, to convert centimeters to millimeters, we need to multiply the given measurement by 10. This will give us the equivalent measurement in millimeters.
Example:
If we are given a length of 5 centimeters, we can convert it to millimeters by multiplying 5 by 10. This gives us a length of 50 millimeters.
It is important to understand the conversion factors between different units of measurement in order to accurately convert measurements from one unit to another. This problem enables us to practice using conversion factors and reinforces our understanding of the relationship between different units of measurement.
Problem 7: Solve a Quadratic Equation
x = (-b ± √(b^2 – 4ac)) / (2a)
In Problem 7, we are given a quadratic equation and need to find its solutions. Let’s solve it step by step:
- Given quadratic equation: ax^2 + bx + c = 0
- Identify the values of a, b, and c.
- Calculate the discriminant: D = b^2 – 4ac.
- Check the value of the discriminant:
- If D > 0, the equation has two distinct real roots.
- If D = 0, the equation has one real root (repeated).
- If D < 0, the equation has no real solutions (complex roots).
- If the equation has real solutions:
- Calculate the values of x using the quadratic formula.
- Plug in the values of a, b, c, and the discriminant into the formula.
- Simplify and solve for x.
- Write down the solutions for the quadratic equation.
By following these steps, we can find the solutions to any quadratic equation. It is important to pay attention to the discriminant, as it determines the nature of the solutions – whether they are real, repeated, or complex.
Problem 8: Graph a Linear Function
In this problem, we are asked to graph a linear function. A linear function is a function that can be represented by a straight line on a Cartesian coordinate system. This type of function is defined by an equation in the form y = mx + b, where m is the slope of the line and b is the y-intercept.
Let’s consider an example to illustrate how to graph a linear function. Suppose we have the equation y = 2x + 3. In this case, the slope of the line is 2 and the y-intercept is 3. To graph this function, we can start by plotting the y-intercept, which is the point (0, 3) on the coordinate plane.
Next, we can use the slope to find additional points on the line. The slope tells us how much the y-coordinate changes for every one unit increase in the x-coordinate. In this case, for every one unit increase in x, the y-coordinate increases by 2. So we can find another point on the line by moving one unit to the right from the y-intercept and two units up.
We can continue this process to find more points on the line. Once we have several points, we can connect them with a straight line to graph the linear function. In this example, the line would have a positive slope, meaning it slopes upward from left to right.