
Welcome to lesson 2 of the Skills Practice: Congruence series. In this lesson, we will be exploring the concept of congruent shapes and how to determine if two shapes are congruent or not. Congruent shapes are shapes that are identical in size and shape, meaning they have the same measurements and angles. In order to determine if two shapes are congruent, we will be using various congruence postulates and theorems.
The answer key provided in this article will help you check your answers and understand the solutions to the practice problems in lesson 2. It is important to review and understand the answer key in order to reinforce your understanding of congruence and improve your problem-solving skills. The answer key includes step-by-step explanations and diagrams to guide you through the process of determining congruence.
By practicing and understanding the concepts and techniques presented in this answer key, you will be better equipped to apply them in real-life situations. Congruence is an important concept in various fields, including architecture, design, and engineering. Developing a strong foundation in congruence will not only help you excel in mathematics but also in these real-world applications.
Lesson 2 Skills Practice Congruence Answer Key
In this lesson, we will review the concept of congruence and explore the answer key for the skills practice exercises. Congruence is a geometric concept that refers to the matching of corresponding sides and angles in two or more objects. When two objects are congruent, they have the same shape and size.
Let’s start by reviewing the answer key for the skills practice exercises. The answer key provides the correct answers to the questions and helps you check your understanding of the material. It is important to carefully study the answer key and compare your answers to ensure accuracy.
Here are some key points from the answer key:
- Exercise 1: In this exercise, you were asked to identify congruent segments and angles. The answer key provides the correct pairs of congruent segments and angles.
- Exercise 2: This exercise focused on congruent triangles. The answer key lists the pairs of congruent sides and angles for each triangle.
- Exercise 3: In this exercise, you were asked to determine if a statement was true or false based on the given information. The answer key provides the correct answers for each statement.
- Exercise 4: This exercise involved proving that two triangles are congruent using the given information. The answer key outlines the steps to complete the proof and provides the correct congruence statement.
By carefully reviewing the answer key and understanding the correct answers, you can improve your skills in identifying congruent segments, angles, and triangles. Practice is key to mastering this concept, so be sure to use the answer key as a tool for learning and improvement.
Overview of Congruence
Congruence is a fundamental concept in geometry that deals with the equality of geometric figures. When two figures are congruent, it means that they have exactly the same shape and size, even if they may be in different orientations or positions. Congruent figures can be rotated, reflected, or translated, but their overall shape and size remain unchanged. Understanding congruence is essential for solving various geometry problems and proving geometric theorems.
There are several methods to determine if two figures are congruent. One common method is using the properties of triangles. If the corresponding sides and angles of two triangles are equal, then the triangles are congruent. This method, known as the Side-Angle-Side (SAS) congruence criterion, is a useful tool for proving congruence in triangles. Another method is using the properties of quadrilaterals. If the opposite sides and angles of a quadrilateral are equal, then the quadrilateral is congruent. This method, known as the Opposite Sides and Angles (OSA) congruence criterion, is applicable to parallelograms and other quadrilaterals.
In addition to triangles and quadrilaterals, congruence can also be applied to other geometric figures such as circles and polygons. For circles, congruence is determined by the equality of their radii. If two circles have the same radius, they are congruent. For polygons, congruence is determined by the equality of their corresponding sides and angles. If all corresponding sides and angles of two polygons are equal, then the polygons are congruent.
Knowing the concept of congruence allows us to analyze and compare different geometric figures and to make meaningful conclusions about their properties and relationships. It is a fundamental tool in geometry that provides a basis for further exploration and understanding of the subject.
Understanding Congruent Figures
In geometry, congruence refers to the property of two figures having the same size and shape. When two figures are congruent, it means that they can be transformed into each other through a combination of translation (moving), rotation (turning), and reflection (flipping).
Congruent figures have corresponding sides and corresponding angles that are equal in measure. This means that if you were to superimpose one congruent figure onto the other, all their corresponding parts would overlap perfectly. For example, if two triangles are congruent, it means that all their sides and angles are equal in measure.
There are several ways to show that two figures are congruent. One way is through the use of congruence statements, which use symbols to represent congruent parts. For example, if we have two congruent triangles, we can write a congruence statement like this: triangle ABC ≅ triangle XYZ.
Another way to prove congruence is through the use of transformations. By performing the same sequence of translations, rotations, and reflections on one figure as on the other, we can show that they are congruent. This can be done using coordinate geometry or by using physical manipulatives, such as cut-out paper shapes.
Understanding congruent figures is important in geometry, as it allows us to determine whether two shapes are identical or not. It also helps in solving problems involving angles, sides, and other properties of shapes. By applying the concept of congruence, mathematicians and engineers can ensure that structures are accurately replicated, measurements are precise, and designs are consistent.
Identifying Congruent Triangles
Congruent triangles are an important concept in geometry, as they have equal measures of corresponding sides and angles. By identifying congruent triangles, we can determine relationships between various parts of a geometric figure and apply this knowledge to solve problems.
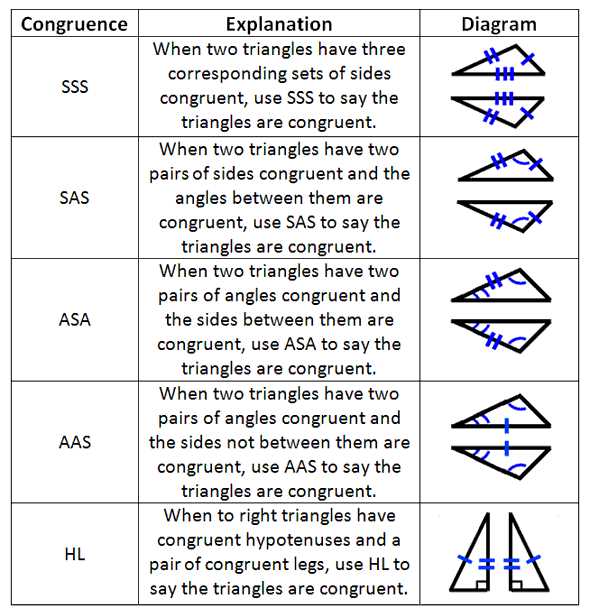
When identifying congruent triangles, there are several key methods we can use. One approach is utilizing the Side-Side-Side (SSS) congruence postulate. This states that if three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent. By comparing the lengths of the sides, we can determine if two triangles are congruent using this postulate.
Another method is the Angle-Angle (AA) congruence postulate. This states that if two angles of one triangle are congruent to two angles of another triangle, then the two triangles are congruent. By comparing the measures of the angles, we can determine if two triangles are congruent using this postulate.
Additionally, we can use the Side-Angle-Side (SAS) congruence postulate. This states that if two sides and the included angle of one triangle are congruent to the corresponding sides and included angle of another triangle, then the two triangles are congruent. By comparing both sides and angles, we can determine if two triangles are congruent using this postulate.
In conclusion, identifying congruent triangles is a vital skill in geometry. By utilizing congruence postulates such as SSS, AA, and SAS, we can determine if two triangles have equal measures of corresponding sides and angles. This knowledge allows us to analyze geometric figures and solve problems more effectively.
Applying Angle Relationships in Congruent Figures

In geometry, congruent figures are figures that have the same shape and size. When dealing with congruent figures, angle relationships play a crucial role in determining their properties and solving problems related to them.
One key concept in applying angle relationships in congruent figures is the idea of corresponding angles. Corresponding angles are angles that are in the same position in relation to the congruent figures. For example, if we have two congruent triangles, the corresponding angles between the two triangles will have the same measurements. This concept allows us to determine the measures of angles in one congruent figure by knowing the angles in another congruent figure.
Another important angle relationship in congruent figures is the concept of vertical angles. Vertical angles are the angles formed by two intersecting lines. They are always congruent, which means they have the same measure. This property can be used to find missing angle measures in a congruent figure by using the measurements of the corresponding vertical angles.
Overall, understanding and applying angle relationships in congruent figures is essential in solving problems related to geometry. By using concepts such as corresponding angles and vertical angles, we can determine the measures of angles in congruent figures and analyze their properties.
Using the Congruence Criteria
When working with congruent figures, it is important to understand the congruence criteria that can be used to determine if two figures are congruent. These criteria allow us to compare corresponding sides and angles of the figures to see if they are equal in size and shape.
One common congruence criterion is the Side-Angle-Side (SAS) criterion. This criterion states that if two sides and the included angle of one triangle are congruent to the corresponding sides and angle of another triangle, then the two triangles are congruent. This criterion is often used when working with right triangles.
Another congruence criterion is the Angle-Angle-Side (AAS) criterion. This criterion states that if two angles and a non-included side of one triangle are congruent to the corresponding angles and side of another triangle, then the two triangles are congruent. This criterion is useful when working with non-right triangles.
It is important to note that these criteria are not the only ways to prove congruence. There are other criteria, such as the Side-Side-Side (SSS) criterion, the Angle-Side-Angle (ASA) criterion, and the Hypotenuse-Leg (HL) criterion, which can also be used to determine if two figures are congruent.
By understanding and applying the congruence criteria, we can confidently determine if two figures are congruent and make accurate geometric proofs.
Solving Problems Involving Congruence

When it comes to solving problems involving congruence, it’s important to understand the concept of congruent figures. Two figures are said to be congruent if they have the same shape and size. This means that all corresponding sides and angles of the figures are equal.
One way to solve problems involving congruence is by using the properties of congruent figures. These properties include the reflexive property of congruence, which states that any figure is congruent to itself. This property can be used to prove congruence by showing that all corresponding sides and angles of the figures are equal.
To solve problems involving congruence, it’s also helpful to know about the different types of transformations that preserve congruence. These transformations include translations, rotations, and reflections. By applying these transformations to figures, you can determine if they are congruent.
- Translations involve sliding a figure without changing its shape or size. If two figures can be translated to coincide with each other, then they are congruent.
- Rotations involve turning a figure around a fixed point. If two figures can be rotated to coincide with each other, then they are congruent.
- Reflections involve flipping a figure across a line. If two figures can be reflected to coincide with each other, then they are congruent.
Using these properties and transformations, you can solve problems that involve congruence by determining if two figures are congruent or not. This can be done by comparing their corresponding sides and angles, as well as performing translations, rotations, and reflections to test for congruence.
In conclusion, solving problems involving congruence requires an understanding of congruent figures, their properties, and different types of transformations. By applying these concepts, you can determine if two figures are congruent and solve problems involving congruence.
Exploring Congruence in Real-World Situations
In the real world, congruence can be found in many different situations. Whether it is in the field of architecture, engineering, or even fashion design, understanding congruence is essential for creating accurate and aesthetically pleasing designs.
Architects use congruence to ensure that structures are built correctly and to scale. By using congruent angles and sides, architects can ensure that a building is symmetrical and balanced. This not only enhances the overall appearance of the building, but also plays a crucial role in its stability and functionality. For example, in designing a bridge, congruent angles and sides are essential for ensuring that the load is evenly distributed and that the structure can withstand the forces acting upon it.
Engineers also rely on congruence in their work. Whether they are designing machinery, vehicles, or electronic devices, engineers must ensure that the components they are working with are congruent. This is important for maintaining the functionality and efficiency of the designs. For instance, in designing a car engine, engineers must ensure that the pistons are congruent to ensure smooth operation and prevent any imbalances that could lead to engine failure.
In the world of fashion design, congruence is crucial for creating well-fitting and visually pleasing garments. Designers must pay attention to congruent measurements and angles in order to create pieces that fit the human body properly. By understanding the principles of congruence, they can ensure that the clothing they create drapes and fits the body in a flattering and comfortable way.
Overall, understanding and applying the concept of congruence in real-world situations is essential for creating accurate, balanced, and functional designs. Whether in architecture, engineering, or fashion design, congruence plays a vital role in achieving successful outcomes.


