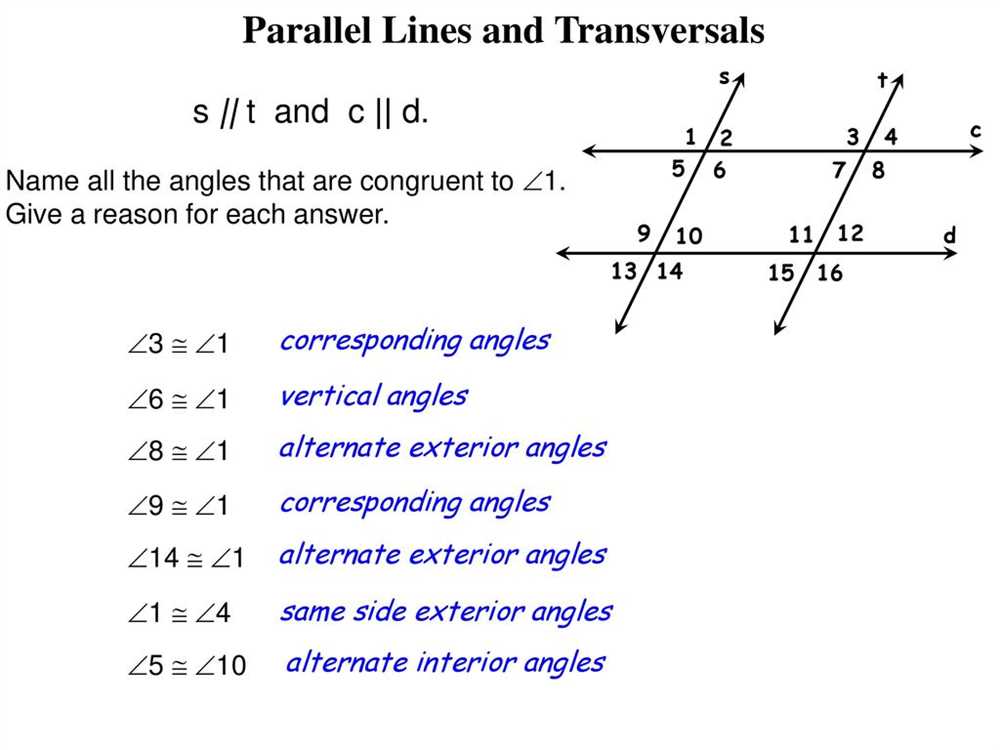
In geometry, transversals and parallel lines are important concepts to understand. When two lines are parallel, they never intersect. Transversals are lines that intersect two or more other lines. In this lesson, we will explore the relationship between transversals and parallel lines and how to find missing angles and identify corresponding angles.
One of the key properties of transversals and parallel lines is that the corresponding angles are congruent. Corresponding angles are the angles that are in the same position on two different lines when intersected by a transversal. For example, if a transversal intersects two parallel lines, the corresponding angles formed on the lines will be congruent.
To solve problems involving transversals and parallel lines, it is important to identify the relationships between angles. This can be done by using the properties of parallel lines and the relationships between corresponding angles. By using the information given, such as the measures of some angles or the relationships between angles, we can determine the measures of missing angles and solve for unknown variables.
What are parallel lines?
Parallel lines are a fundamental concept in geometry. They are two straight lines that never intersect, no matter how far they are extended. In other words, parallel lines never cross each other. This unique characteristic of parallel lines allows them to maintain a constant distance between each other.
To identify parallel lines, you can look for certain properties. One property is that the angles formed by a transversal cutting the parallel lines are congruent. Another property is that the alternate interior, alternate exterior, corresponding, and consecutive interior angles are congruent. These properties can help you determine if lines are parallel or not.
Parallel lines have various applications in the real world. For example, parallel lines are used in architecture to create symmetrical and balanced structures. They are also used in navigation, where parallel lines of latitude help determine the position of a ship or aircraft. Additionally, parallel lines are used in engineering to design railway tracks, ensuring that they never intersect and provide a smooth path for trains to travel on.
In conclusion, parallel lines are an important concept in geometry and have practical applications in various fields. Understanding the properties and characteristics of parallel lines can help solve geometric problems and design efficient structures in the real world.
What are transversals?
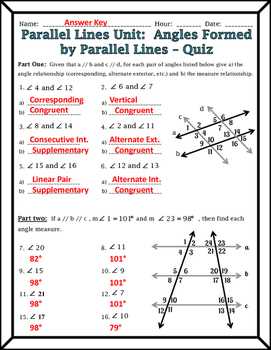
A transversal is a line that intersects two or more parallel lines. When a transversal intersects two parallel lines, it creates eight angles, consisting of two pairs of corresponding angles, two pairs of alternate interior angles, two pairs of alternate exterior angles, and a pair of consecutive interior angles. Understanding the properties and relationships of these angles is important in solving geometry problems involving parallel lines and transversals.
Corresponding angles are located in the same position relative to the transversal and the parallel lines. They are equal in measure. Alternate interior angles are located between the two parallel lines and on opposite sides of the transversal. They are equal in measure. Similarly, alternate exterior angles are located outside the parallel lines and on opposite sides of the transversal. They are also equal in measure. Consecutive interior angles are located inside the parallel lines and on the same side of the transversal. They add up to 180 degrees.
Transversals are an important concept in geometry because they help determine the relationships between angles formed by intersecting lines. They allow us to identify and apply various angle properties, such as the corresponding angles theorem, alternate interior angles theorem, and alternate exterior angles theorem. These theorems can be used to prove statements and solve problems involving parallel lines and transversals.
Identifying Angle Relationships
When working with angles and lines, it is important to understand the relationships between them. By identifying these relationships, we can better understand the properties and characteristics of angles and lines.
One common relationship is that of parallel lines and transversals. When a transversal intersects two parallel lines, it creates a set of corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles. These angle pairs have specific properties and can help us solve problems involving angles and lines.
- Corresponding angles: Corresponding angles are located in the same position relative to the transversal and the parallel lines. They are congruent to each other.
- Alternate interior angles: Alternate interior angles are located on opposite sides of the transversal and between the parallel lines. They are congruent to each other.
- Alternate exterior angles: Alternate exterior angles are located on opposite sides of the transversal and outside the parallel lines. They are congruent to each other.
- Consecutive interior angles: Consecutive interior angles are located on the same side of the transversal and between the parallel lines. They add up to 180 degrees.
By identifying these angle relationships, we can apply them to solve problems involving angles and lines. Whether it’s finding missing angles, proving theorems, or showing congruence between triangles, understanding angle relationships is essential in geometric reasoning and problem-solving.
Corresponding Angles
Corresponding angles are a key concept in geometry, especially when discussing transversals and parallel lines. When two lines are crossed by a third line, known as the transversal, the angles that are in the same relative position are called corresponding angles.
Corresponding angles are formed when a transversal intersects two parallel lines. They lie on opposite sides of the transversal and in the same relative position. These angles have the same degree of measure and can be labeled as corresponding angles using a specific notation.
Notation: Corresponding angles are typically labeled using the same letter in the same position on each intersected line. For example, if angle A and angle B are corresponding angles, they can be denoted as ∠A and ∠B. This notation helps to clearly identify which angles are corresponding.
Corresponding angles have several important properties. Firstly, if two lines are parallel, then their corresponding angles are congruent, meaning they have the same measure. Secondly, corresponding angles can be used to prove that two lines are parallel. If the corresponding angles are congruent, then the lines are parallel. Lastly, corresponding angles can be used to solve geometry problems and find missing angle measures.
Understanding corresponding angles is crucial when studying geometry and the relationship between lines. It allows us to identify congruent angles, prove parallel lines, and solve various geometric problems. Mastering the concept of corresponding angles is essential for success in geometry.
Alternate Interior Angles

Alternate interior angles are a type of angle formed when a transversal intersects two parallel lines. They lie on the inside of the parallel lines and on opposite sides of the transversal. These angles are equal in measure.
When a transversal intersects two parallel lines, it creates eight angles. Alternate interior angles are formed by the transversal crossing inside the parallel lines, diagonal to each other. These angles are called “alternate” because they are located on opposite sides of the transversal. They are also called “interior” because they are inside the parallel lines.
The alternate interior angles theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles formed are congruent. This means that their measures are equal. Therefore, if one angle measures x degrees, the other alternate interior angle will also measure x degrees.
Knowing about alternate interior angles can be useful in various geometric proofs and problem-solving scenarios. By recognizing these angles and their properties, we can determine the relationships between different angles and lines within a given figure. It helps us understand angles formed by intersecting lines and parallel lines.
In summary, alternate interior angles are a type of angle formed by a transversal intersecting two parallel lines. They are located on the inside of the parallel lines and on opposite sides of the transversal. These angles are equal in measure, as stated by the alternate interior angles theorem.
Alternate Exterior Angles:
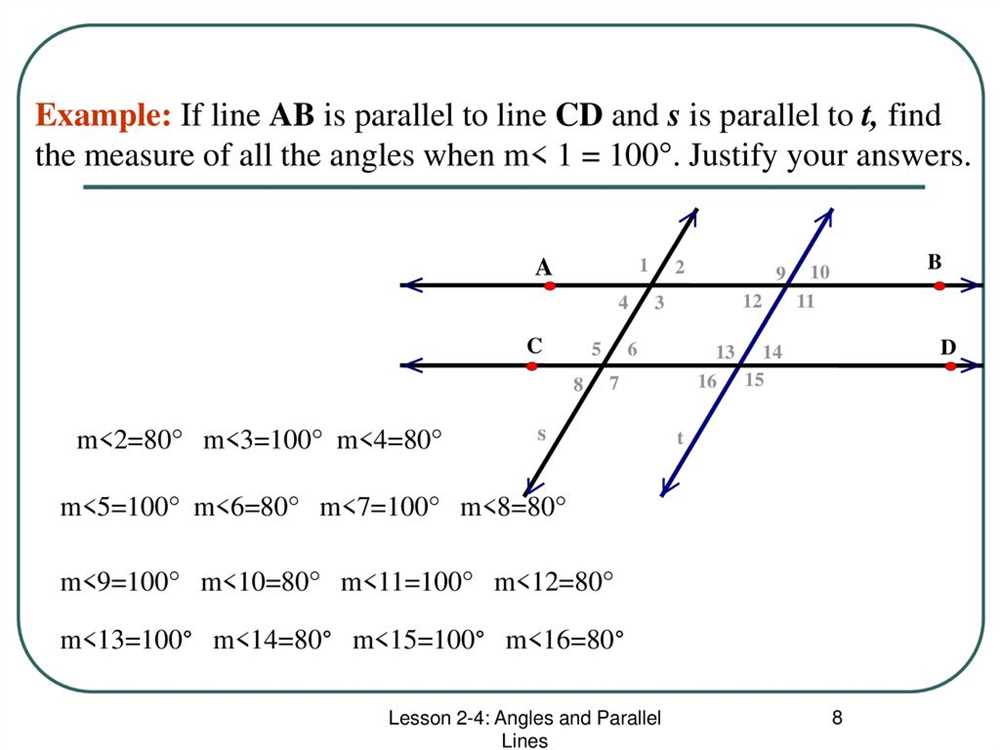
Alternate exterior angles are a fundamental concept in the study of geometry and are formed when a transversal intersects two parallel lines. In this case, alternate exterior angles are located on opposite sides of the transversal and outside the two parallel lines.
One important property of alternate exterior angles is that they are congruent. This means that if two parallel lines are intersected by a transversal, then the corresponding alternate exterior angles will have the same measure. This property can be proved using the corresponding angle postulate or the alternate exterior angles theorem.
Corresponding Angle Postulate: If a transversal intersects two parallel lines, then the corresponding angles are congruent.
Alternate Exterior Angles Theorem: If a transversal intersects two parallel lines, then the alternate exterior angles are congruent.
This property of congruent alternate exterior angles can be used to solve various problems in geometry, such as finding missing angle measures or proving the congruence of two triangles. It is an important concept to understand and apply in the study of parallel lines and transversals.
Solving Problems with Parallel Lines and Transversals
When working with parallel lines and transversals, one of the key concepts to understand is the relationship between the angles formed. By identifying specific angle pairs, we can solve various geometric problems efficiently.
First, it is important to understand the difference between alternate interior angles, corresponding angles, and vertical angles. Alternate interior angles are pairs of angles that are on opposite sides of the transversal and between the parallel lines. Corresponding angles are pairs of angles that are in the same position relative to the transversal and the parallel lines. Vertical angles are pairs of angles that are opposite each other and formed by intersecting lines.
Using these angle relationships, we can solve problems involving parallel lines and transversals. For example, if we are given two parallel lines intersected by a transversal and asked to find the measure of a specific angle, we can identify the corresponding angles or alternate interior angles to determine the value. By applying the properties of angles formed by parallel lines and a transversal, we can easily find the solution.
In addition to finding angle measures, parallel lines and transversals can be used to solve other types of problems as well. For instance, we can determine if two lines are parallel by analyzing the angles formed by a transversal. If the alternate interior angles or corresponding angles are congruent, then the lines are parallel. This property can be applied in real-life situations, such as determining if two roads are parallel or if two railway tracks are parallel.
In conclusion, understanding the properties and relationships of angles formed by parallel lines and transversals is essential in solving various geometric problems. Whether finding angle measures or identifying parallel lines, these concepts can be applied to real-life scenarios as well. By recognizing the patterns and using the angle relationships, we can effectively solve problems involving parallel lines and transversals.
Using Angle Relationships to Find Missing Angles
In geometry, angle relationships are an important concept when it comes to finding missing angles. By understanding the properties and relationships between angles, we can solve for unknown angles in a variety of situations.
One common angle relationship is the vertical angles theorem. It states that when two lines intersect, their opposite angles are congruent. This means that if we know the measure of one angle formed by intersecting lines, we can determine the measure of the other angle by simply setting them equal to each other.
Another important angle relationship is the corresponding angles theorem. It states that when a transversal intersects two parallel lines, the corresponding angles formed are congruent. This means that if we have a pair of corresponding angles, we can set them equal to each other to solve for the unknown angle.
The alternate interior angles theorem is yet another angle relationship that can be used to find missing angles. It states that when a transversal intersects two parallel lines, the alternate interior angles are congruent. By identifying alternate interior angles in a figure, we can set them equal to each other and solve for the unknown angle.
In addition to these theorems, there are many other angle relationships that can be used to find missing angles, such as the alternate exterior angles theorem, the consecutive interior angles theorem, and the supplementary angles theorem. By understanding and applying these angle relationships, we can effectively solve for unknown angles and deepen our understanding of geometric properties.
Applying Parallel Lines and Transversals in Real-life Situations
In the study of geometry, parallel lines and transversals are often abstract concepts that are explored in a theoretical setting. However, these concepts have practical applications in real-life situations as well. Understanding parallel lines and transversals can be helpful in various fields such as architecture, engineering, and design.
One practical application of parallel lines and transversals is in the construction industry. Architects and engineers use these concepts to design and build structures that are stable and aesthetically pleasing. By applying the principles of parallel lines and transversals, they can ensure that beams, columns, and walls are placed correctly and aligned parallel to each other. This not only enhances the structural integrity of the building but also creates a visually appealing design.
Another real-life situation where parallel lines and transversals come into play is in road construction. Highway engineers often need to construct roads that are parallel to existing structures, such as buildings or rivers. By understanding and applying the principles of parallel lines and transversals, they can ensure that the road follows a straight path and maintains a consistent distance from these structures. This not only improves the functionality of the road but also minimizes the impact on surrounding structures.
Parallel lines and transversals are also relevant in the field of interior design. Designers often use these concepts to create visually pleasing spaces by arranging furniture, artwork, and decor in a harmonious manner. By applying the principles of parallel lines and transversals, they can create balanced and symmetrical designs that are aesthetically pleasing to the eye. This can result in a more enjoyable and comfortable living or working environment.
In conclusion, parallel lines and transversals have practical applications in various real-life situations. Whether it’s in architecture, engineering, road construction, or interior design, understanding these concepts can help professionals create structures and spaces that are functional, visually appealing, and harmonious. By applying the principles of parallel lines and transversals, professionals can ensure accuracy, stability, and aesthetics in their work.